2019. 4. 10. 21:56, 워게임/root-me.org
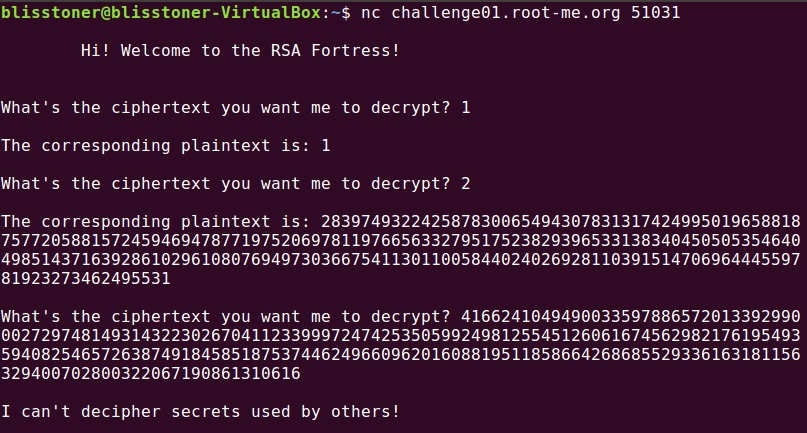
내가 입력한 값에 $d$승을 해서 넘겨주는 것 같습니다. 당연하게도 $C$를 보내면 해독을 해주지 않습니다. 그런데 $(-C)$를 보내서 $(-C)^d$를 받았다고 생각해봅시다. $d$는 홀수이니 $n-(-C)^d = C^d=P$가 됩니다. 즉 $n-C$를 보내고 받은 값과 $n$의 차가 곧 평문입니다.
import base64
def gcd(a, b):
if a == 0: return b
return gcd(b%a, a)
def egcd(a, b):
if a == 0:
return (b, 0, 1)
g, y, x = egcd(b%a,a)
return (g, x - (b//a) * y, y)
def inv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('No modular inverse')
return x%m
n = 456378902858290907415273676326459758501863587455889046415299414290812776158851091008643992243505529957417209835882169153356466939122622249355759661863573516345589069208441886191855002128064647429111920432377907516007825359999
c = 41662410494900335978865720133929900027297481493143223026704112339997247425350599249812554512606167456298217619549359408254657263874918458518753744624966096201608819511858664268685529336163181156329400702800322067190861310616
e = 0x10001
print(n-c)
p = n-456378902858290907415273676326459758501863587455889046415299414290812776158851091008643992243505529957417209835882169153356466938393414751212578993778062169206279587246489607610095558673805072417440334109998729068241749598484
print(p.to_bytes(200,'big'))'워게임 > root-me.org' 카테고리의 다른 글
| [Cryptanalysis] Initialisation Vector (0) | 2019.04.23 |
|---|---|
| [Cryptanalysis] Service - Timing attack (0) | 2019.04.10 |
| [Cryptanalysis] RSA - Factorisation (0) | 2019.04.10 |
| [Cryptanalysis] LFSR - Known plaintext (0) | 2019.04.10 |
| [Cryptanalysis] AES - ECB (0) | 2019.04.04 |
| [Cryptanalysis] AES - CBC - Bit-Flipping Attack (0) | 2019.03.19 |
Comments