------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
현재 보고있는 강의는 구버전입니다. 내용에는 문제가 없으나 리뉴얼 중이니 이 게시글을 참고해주세요.
리뉴얼한 버전은 [실전 알고리즘] 0x1D강 - 다익스트라 알고리즘에서 확인할 수 있습니다. 리뉴얼 버전으로 보시는 것을 추천드립니다.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

안녕하세요, 드디어 마지막 강입니다. 매우 신이 납니다. 다익스트라 알고리즘으로 마지막을 장식하고 강의를 완결내도록 하겠습니다.

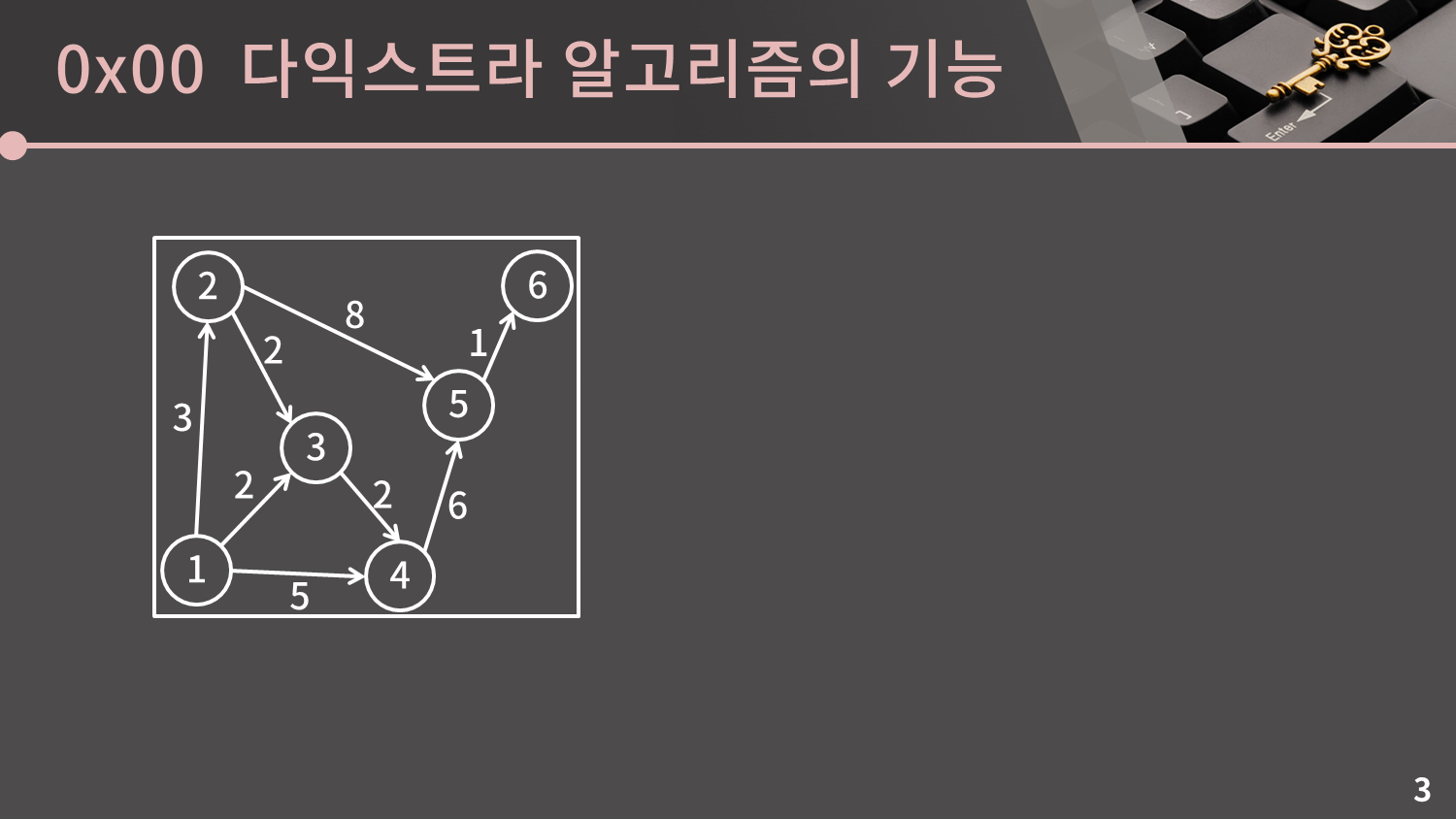
맨날 보던 그래프만 또 보면 지겨울까봐 이번에는 조금 다른 모양의 방향 그래프를 준비했습니다. 다익스트라 알고리즘은 방향 그래프 혹은 무방향 그래프에서 하나의 시작점로부터 다른 모든 정점 까지의 최단 거리를 구해주는 알고리즘입니다. 단, 음수의 가중치를 가지는 간선이 포함되어 있을 때에는 사용할 수 없습니다.
학부 알고리즘 수업에서 반드시 다루는 알고리즘이기 때문에 적어도 이름과 그 목적만큼은 꽤 유명하나 구현에서 실수를 할 수 있는 여지가 굉장히 많기에 다익스트라 알고리즘에 대해 어렴풋이 알고만 있고 구현에 자신이 없다면 이번 기회에 확실하게 익혀봅시다.
참고로 실무에서 개발을 많이 해보신 분이라면 길찾기 알고리즘의 대표적인 예시로 A*(A star) 알고리즘이라는 것을 들어본 적이 있을 것입니다. BOJ에서 길찾기 관련 문제가 나올 때 A* 알고리즘을 찾아보는 경우를 몇 번 본적이 있습니다. A* 알고리즘은 다익스트라 알고리즘의 휴리스틱을 더해 시간복잡도를 효율적으로 한 대신 100% 정확한 답을 보장하지는 않는 알고리즘입니다. 네비게이션에서의 길찾기 등과 같이 100% 정확한 답을 내지 않아도 되고, 또 정점의 갯수가 너무 많아 현실적으로 다익스트라 알고리즘을 사용하기 힘들 경우에 유용하게 사용할 수 있습니다. 그러나 코딩테스트에서는 휴리스틱을 요구하지 않기 때문에 A* 알고리즘을 알 필요가 없고 다익스트라 알고리즘만 익히면 됩니다.

그 어떤 시작점을 잡아도 상관없지만 제 마음대로 1번 정점을 시작점으로 잡겠습니다. 이 때 1번 정점에서 다른 정점들까지 가는데 필요한 거리는 테이블과 같습니다.
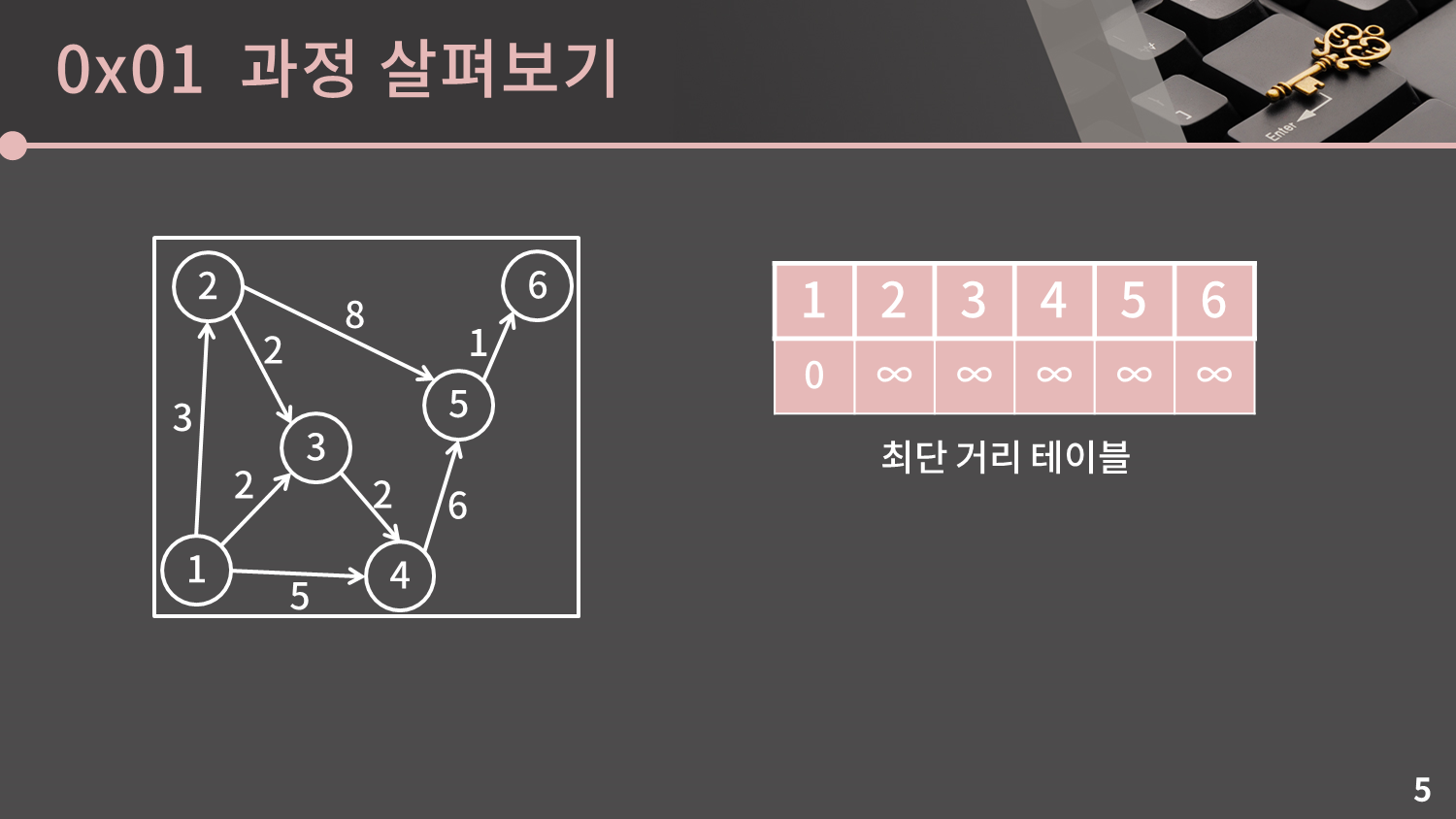
이제 다익스트라 알고리즘의 과정을 알아보겠습니다. 설명을 돕기 위해 그래프와 거리가 ∞으로 초기화된 빈 테이블을 모셔왔습니다. 단, 자기 자신과의 거리는 0일테니 1번 인덱스의 값은 0으로 둡니다.
다익스트라 알고리즘은 매 단계마다 남아있는 정점 중에서 시작점으로부터의 거리가 가장 가까운 정점을 구하고, 시작점으로부터 해당 정점까지의 거리를 확정하는 방식입니다. 말 뜻이 잘 이해가 안 갈수도 있는데, 과정을 한 번 보고 나면 이해가 갈 것입니다.
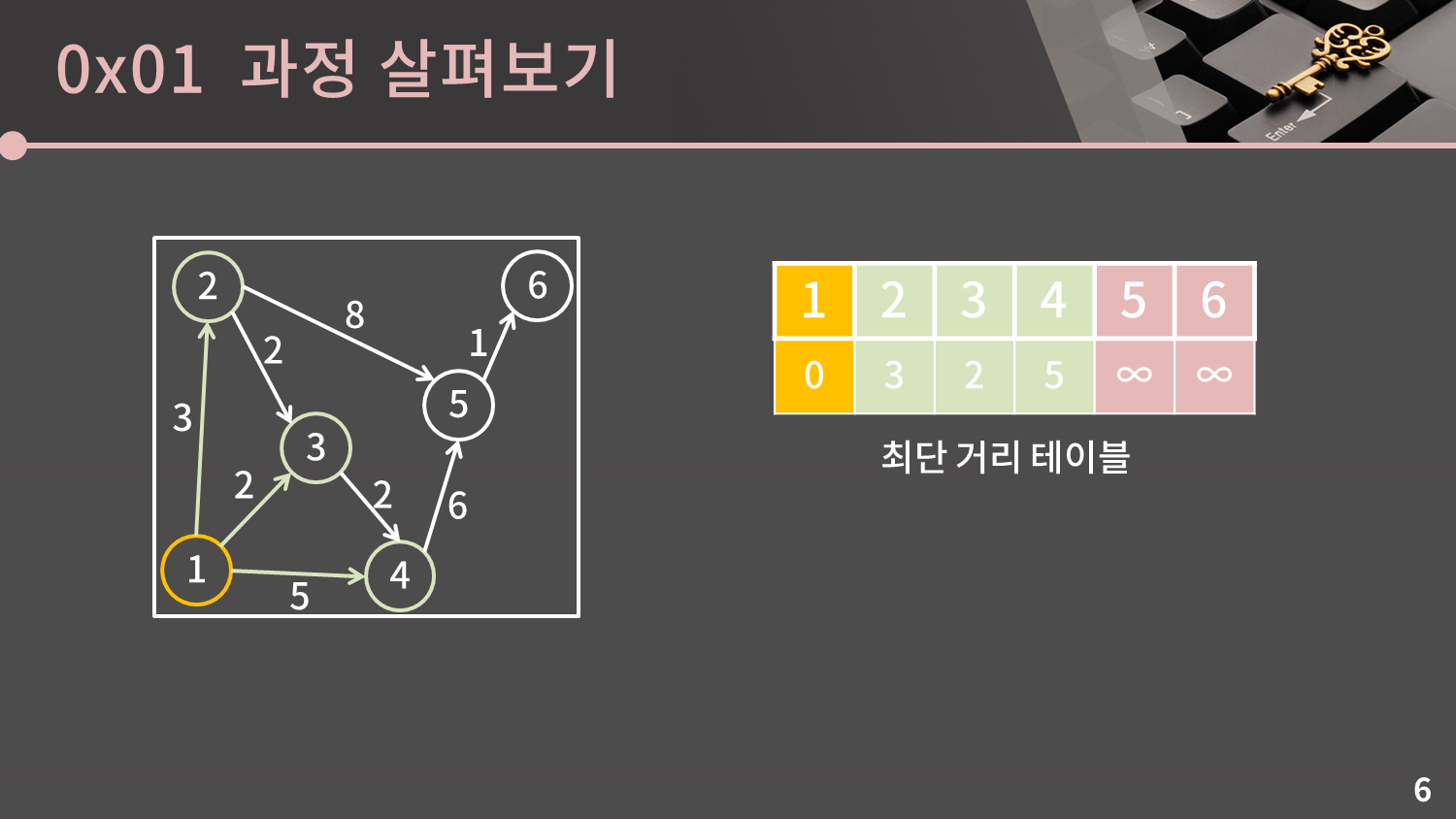
현재 1, 2, 3, 4, 5, 6번 정점이 모두 남아있습니다. 이 중에서 시작점으로부터 1번 정점까지의 거리는 0이고 1번 정점을 제외한 나머지 정점과의 거리는 현재 ∞이므로 남아있는 정점 중에서 1번 정점까지의 거리가 가장 가깝습니다. 1번 정점까지의 거리는 0으로 확정됩니다.
일단 시작점과 1번 정점의 거리는 0이고, 1번 정점에서 2, 3, 4번 정점으로 갈 수 있기 때문에 1번 정점을 거쳐서 2, 3, 4번 정점으로 갈 때의 최단 거리는 1번 정점까지의 거리와 간선의 가중치를 합쳐 각각 $0+3=3$, $0+2=2$, $0+5=5$이 됩니다. 이 값과 기존에 저장된 값 중 작은 것을 최단 거리 테이블에 쓰면 됩니다. 기존에는 모두 ∞이 저장되어 있었으므로 각각 3, 2, 5로 갱신을 해줍니다.
주황색은 시작점으로부터의 거리가 확정된 정점을, 초록색은 이번에 확정된 정점으로부터 들어오는 간선이 있어 최단거리가 변경될 수 있는 정점을 의미합니다.

현재 2, 3, 4, 5, 6번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 2인 3번 정점입니다. 3번 정점까지의 거리는 2로 확정됩니다.
일단 시작점과 3번 정점의 거리는 2이고, 3번 정점에서 4번 정점으로 갈 수 있기 때문에 3번 정점을 거쳐서 4번 정점으로 갈 때의 최단 거리는 3번 정점까지의 거리와 간선의 가중치를 합쳐 $2+2=4$가 됩니다. 이 값과 기존에 저장된 값 중 작은 것을 최단 거리 테이블에 쓰면 됩니다. 기존에는 4번 정점까지의 최단 거리가 5로 저장되어 있었으므로 이를 4로 갱신합니다.

현재 2, 4, 5, 6번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 3인 2번 정점입니다. 2번 정점까지의 거리는 3으로 확정됩니다.
일단 시작점과 2번 정점의 거리는 3이고, 2번 정점에서 3, 5번 정점으로 갈 수 있기 때문에 2번 정점을 거쳐서 3, 5번 정점으로 갈 때의 최단 거리는 3번 정점까지의 거리와 간선의 가중치를 합쳐 각각 $3+2=5$, $3+8=11$이 됩니다. 이 값과 기존에 저장된 값 중 작은 것을 최단 거리 테이블에 쓰면 됩니다. 3번 정점의 경우 기존의 값이 더 작으므로 아무 일도 일어나지 않습니다. 5번 정점의 경우 기존에는 ∞이 저장되어 있었으므로 이를 11로 갱신합니다.
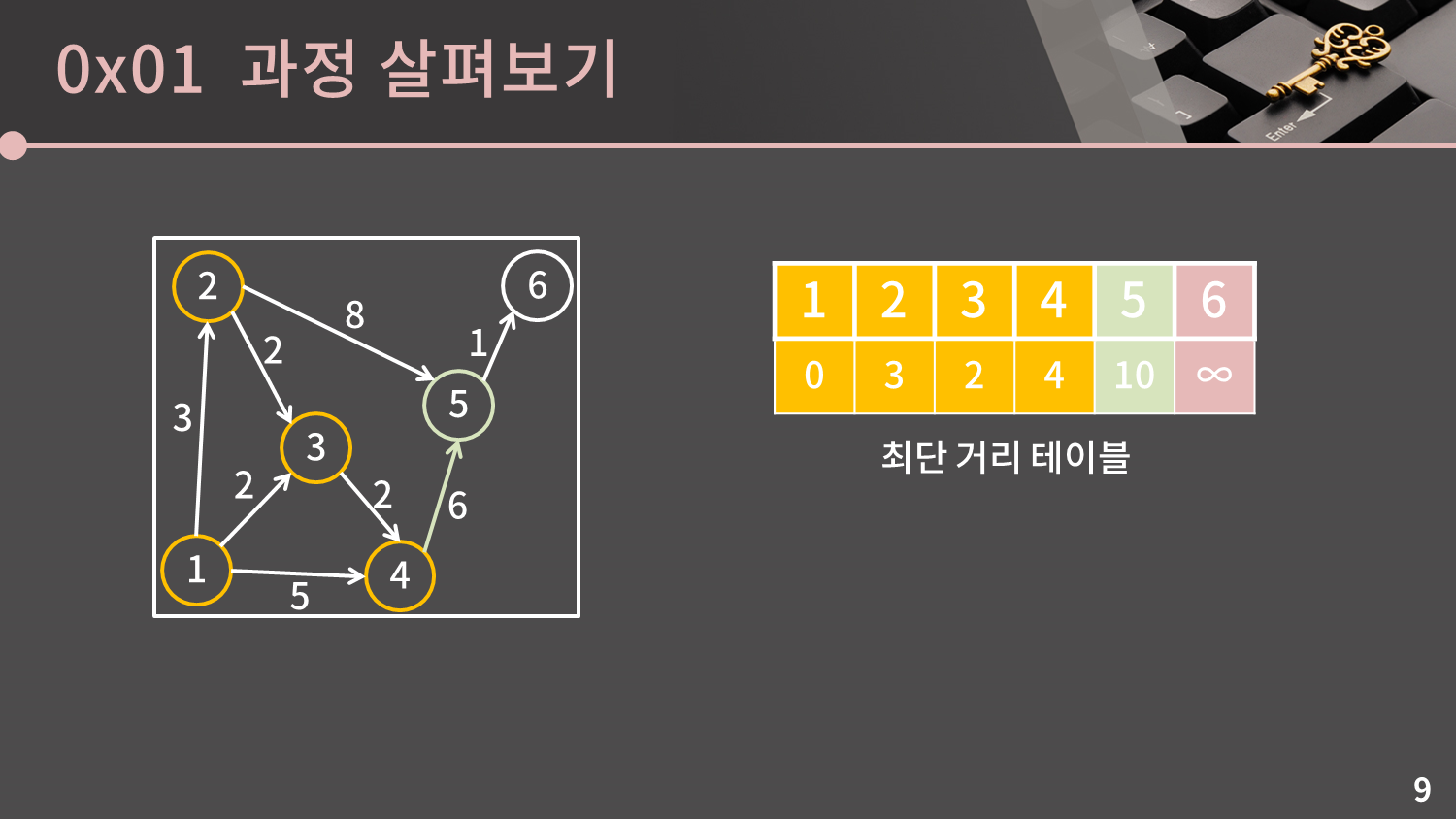
현재 4, 5, 6번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 4인 4번 정점입니다. 4번 정점까지의 거리는 4로 확정됩니다.
일단 시작점과 4번 정점의 거리는 4이고, 4번 정점에서 5번 정점으로 갈 수 있기 때문에 4번 정점을 거쳐서 5번 정점으로 갈 때의 최단 거리는 4번 정점까지의 거리와 간선의 가중치를 합쳐 $4+6=10$이 됩니다. 이 값과 기존에 저장된 값 중 작은 것을 최단 거리 테이블에 쓰면 됩니다. 기존에는 5번 정점까지의 최단 거리가 11으로 저장되어 있었으므로 이를 10로 갱신합니다.

현재 5, 6번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 10인 5번 정점입니다. 5번 정점까지의 거리는 10으로 확정됩니다.
일단 시작점과 5번 정점의 거리는 10이고, 5번 정점에서 6번 정점으로 갈 수 있기 때문에 5번 정점을 거쳐서 6번 정점으로 갈 때의 최단 거리는 4번 정점까지의 거리와 간선의 가중치를 합쳐 $10+1=11$이 됩니다. 이 값과 기존에 저장된 값 중 작은 것을 최단 거리 테이블에 쓰면 됩니다. 기존에는 5번 정점까지의 최단 거리가 ∞으로 저장되어 있었으므로 이를 11로 갱신합니다.
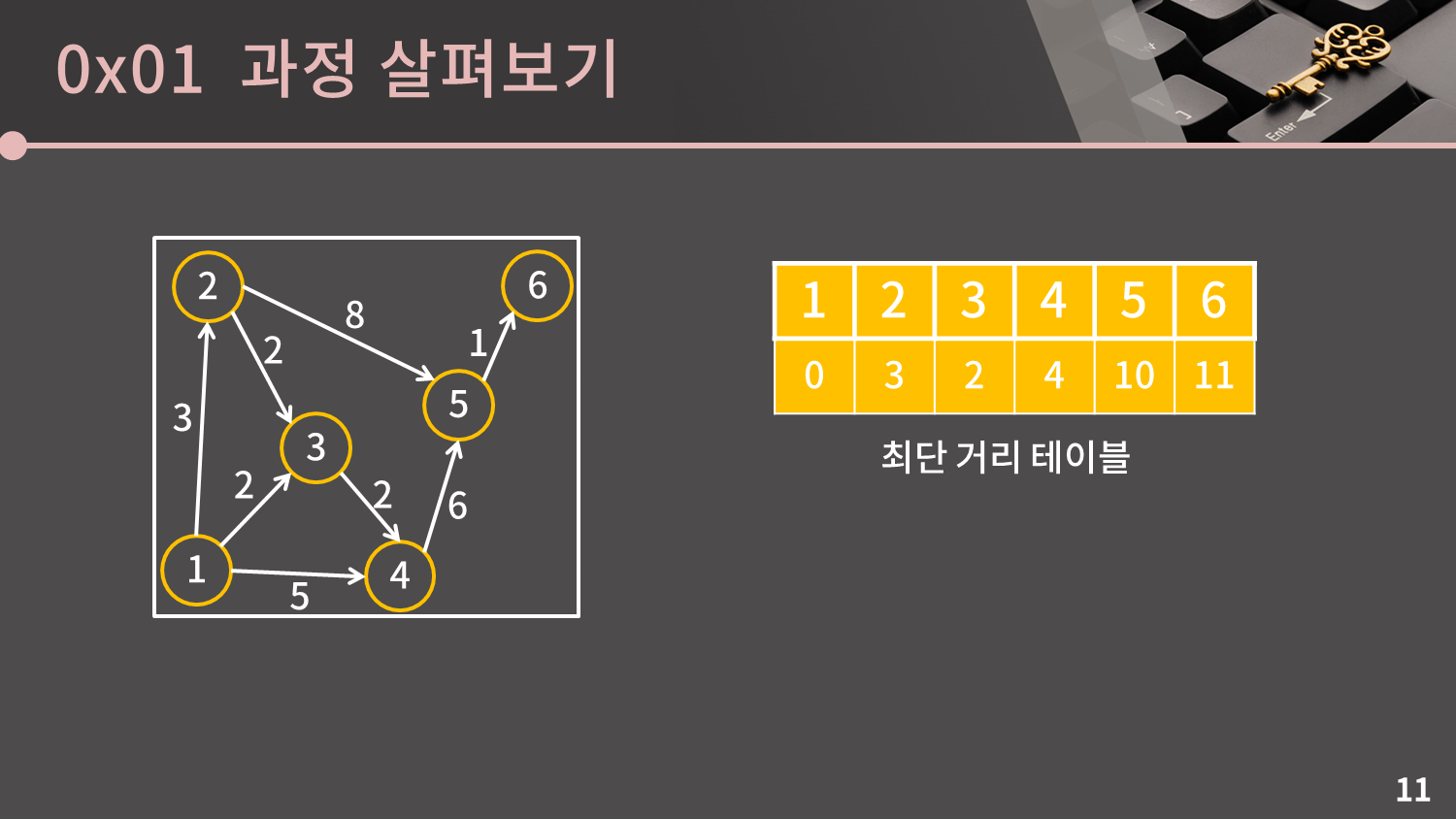
현재 6번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 11인 6번 정점입니다. 6번 정점까지의 거리는 11로 확정됩니다.
시작점으로부터 모든 정점까지의 거리가 정해졌으므로 알고리즘이 종료됩니다. 어떤가요? 엄청 어렵지는 않죠?
요약하면 매 단계마다 최단 거리 테이블을 확인해 가장 가까운 것을 찾고, 그 것과 인접한 정점들에 대해 최단 거리 값을 갱신해주는 작업을 반복해주면 됩니다.
일단 곧이곧대로 구현을 한다고 해봅시다. $V$번에 걸쳐 진행되는 각 단계마다 현재 남아있는 모든 정점에 대해 최단 거리 테이블을 확인해 최소값을 뽑아내야 하기에 $O(V)$가 필요하고 이것이 $V$번 발생하므로 $O(V^2)$입니다. 또한 각 단계마다 자신으로부터 나가는 모든 간선에 대해 최단 거리 테이블의 갱신을 위한 연산이 발생합니다. 예를 들어 5에서 6으로 가는 간선을 생각할 때, 5번 정점까지의 최단 거리를 확정지은 후 6번 정점까지의 최단 거리를 $10+1=11$로 갱신했던 것과 같은 일을 말합니다. 이 과정에서 만약 그래프를 인접 리스트로 저장하고 있었다면 $O(E)$가, 인접 행렬로 저장하고 있었다면 $O(V^2)$가 필요합니다. 인접 리스트 상황을 가정했을 때 곧이곧대로 구현한 다익스트라 알고리즘의 시간복잡도는 $O(V^2+E)$입니다.
그런데 힙을 사용하면 시간복잡도를 $O(ElgE)$로 만들 수 있습니다. 만약 $E$가 $V^2$에 가깝다면 오히려 $O(V^2+E)$가 더 효율적일 수 있겠지만 다익스트라 알고리즘을 요구하는 문제의 경우에는 $V$는 3만, $E$는 10만 정도와 같이 힙을 이용해 구현해야 통과할 수 있고 그렇지 않을 경우 시간 초과가 발생하게끔 설계한 경우가 많습니다.
힙을 이용한 구현은 안타깝게도 헷갈릴 수 있는 여지가 많습니다. 구글이나 네이버에 검색해서 나오는 수많은 다익스트라 알고리즘 코드들 중에서도 잘못 구현된 것이 꽤 많습니다. 잘못 구현할 경우 시간복잡도가 지수로 가버리거나, 잘못된 답을 내거나 할 수 있으니 이번에 제대로 배워가시면 좋겠습니다.

힙을 이용한 다익스트라의 구현을 다루기 전에 왜 음수 간선이 있을 때 문제가 생기는지를 짚고 넘어가겠습니다. 이해를 돕기 위해 아주 간단한 형태의 그래프를 준비했습니다. 테이블의 초기 값도 올바르게 세팅을 해두었습니다. 시작점은 1번 정점입니다.

현재 1, 2, 3번 정점이 남아있습니다. 이 중에서 시작점으로부터 1번 정점까지의 거리는 0이고 1번 정점을 제외한 나머지 정점과의 거리는 현재 ∞이므로 남아있는 정점 중에서 1번 정점까지의 거리가 가장 가깝습니다. 1번 정점까지의 거리는 0으로 확정됩니다.
2, 3번 정점의 최단 거리는 각각 3과 2로 갱신됩니다.

현재 2, 3번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 2인 3번 정점입니다. 3번 정점까지의 거리는 2으로 확정됩니다.
3번 정점에서 나가는 간선이 없으므로 갱신은 발생하지 않습니다.

현재 2번 정점이 남아있습니다. 이 중에서 시작점으로부터 가장 가까운 점은 거리가 3인 2번 정점입니다. 2번 정점까지의 거리는 3로 확정됩니다.
시작점으로부터 모든 정점까지의 거리가 정해졌으므로 알고리즘이 종료됩니다.
그런데 뭔가 이상합니다. 1 -> 2 -> 3이라는 경로를 따라가면 $3+(-5)=-2$ 만에 정점 3에 도달할 수 있는데 최단 거리 테이블에는 2라고 되어있습니다. 즉 잘못된 답을 냈네요.
음수 간선이 있어서 남아있는 정점 중에서 시작점으로부터의 거리가 가장 가까운 정점을 구하더라도 시작점으로부터 해당 정점까지의 거리가 확정되지 않고 지금의 3번 정점과 같이 음수 정점으로 인해 거리가 더 줄어들 수 있기 때문에 다익스트라 알고리즘이 제대로 동작하지 않는 것입니다.
음수 간선을 포함한 그래프는 벨만 포드 알고리즘을 이용해 하나의 시작점로부터 다른 모든 정점 까지의 최단 거리를 구할 수 있습니다. 해당 알고리즘을 이 강의에서는 다루지 않을 예정이기 때문에 궁금하다면 직접 찾아보세요. 저희는 음수 간선이 있을 땐 다익스트라 알고리즘을 사용해서는 안된다는 사실만 기억합시다.

이제 힙을 이용한 다익스트라 알고리즘의 구현을 소개해드리겠습니다. 일단 방법은
1. 힙에 (0, 시작점)을 넣는다.
2. 힙에서 거리가 가장 작은 원소를 꺼낸다. 해당 거리가 최단 거리 테이블에 있는 값과 다를 경우에는 아무 동작도 하지 않는다.
3. 원소가 가리키는 정점을 u라고 하자. u와 이웃한 정점들에 대해 최단 거리 테이블 값보다 u를 거쳐가는 것이 더 작은 값을 가질 경우 최단 거리 테이블의 값을 갱신하고 힙에 (거리, 이웃한 정점의 번호)를 추가한다.
4. 힙이 빌 때 까지 2, 3번 과정을 반복한다.
입니다. 개념이 크게 어렵지 않다면 바로 코드를 보여드리면서 설명드릴텐데, 어려워하실 것 같아 구현에 초점을 맞춰 다시 과정을 따라가보겠습니다.
일단 최단 거리 테이블은 처음처럼 0과 ∞으로 채워두겠습니다.

이제 힙을 이용한 다익스트라 알고리즘의 구현을 소개해드리겠습니다. 개념이 크게 어렵지 않다면 바로 코드를 보여드리면서 설명드릴텐데, 어려워할 것 같아 구현에 초점을 맞춰 다시 과정을 따라가보겠습니다.
일단 최단 거리 테이블은 처음처럼 0과 ∞으로 채워두겠습니다.

힙을 이용한 구현에서는 맨 처음에 추가로 해줘야할 것이 있는데, 바로 (0, 시작점)을 힙에 넣어주는 것입니다. 구현을 할 때에는 STL pair를 힙에 삽입할 것입니다. 이 때 first는 거리를 의미하고 second는 정점의 번호를 의미합니다.
초기 세팅은 완료됐습니다. 과정을 시작해봅시다.

힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (0, 1)이 선택될 것입니다. 편의상 최단 거리 테이블을 $d$ 테이블이라고 하겠습니다. 우선 $d[1] = 0$이 맞는지 확인합니다. 만약 일치하지 않는다면 해당 원소를 제거하고 넘어갈 것이지만 지금은 일치하므로 과정을 이어갑니다.

일단 시작점과 1번 정점의 거리는 0이고, 1번 정점에서 2, 3, 4번 정점으로 갈 수 있기 때문에 1번 정점을 거쳐서 2, 3, 4번 정점으로 갈 때의 최단 거리는 1번 정점까지의 거리와 간선의 가중치를 합쳐 각각 $0+3=3$, $0+2=2$, $0+5=5$이 됩니다. 이 값이 $d$ 테이블에 저장된 값보다 작을 경우 최단 거리 테이블에 쓰고 힙에 삽입을 해줍니다. 기존에는 모두 ∞이 저장되어 있었으므로 각각 3, 2, 5로 갱신을 해주면서 힙에 삽입합니다.
지금 (2, 3), (3, 2)가 조금 혼동을 줄 수 있을 것 같은데 왼쪽이 거리고 오른쪽이 정점의 번호입니다. 즉 힙의 2번째 원소는 거리가 2이고 3번 정점에 관한 원소라는 의미입니다. 헷갈리지 마세요.

모든 처리가 끝났으니 (0, 1) 원소를 제거합니다. 엄밀히 말해서는 BFS, DFS에서 하듯 top()을 임시 변수에 넣은 후 바로 제거를 하지만, 서술의 편의를 위해 과정이 끝난 후 원소를 제거하는 것으로 작성해두었습니다.
처음에 과정을 소개할 땐 거리가 확정된 정점을 주황색으로 나타냈는데 기억하시나요? 이와 달리 힙을 이용한 구현에서는 거리가 확정된 정점인지에 대한 여부를 따로 관리하지 않습니다. 마저 살펴보면 이해가 가겠지만, 어차피 거리가 확정된 정점은 더 이상 최단 거리 테이블의 갱신이 이루어지지 않기 때문입니다.

힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (2, 3)이 선택될 것입니다. 우선 $d[3] = 2$가 맞는지 확인합니다. 일치하므로 과정을 이어갑니다.

일단 시작점과 3번 정점의 거리는 2이고, 3번 정점에서 4번 정점으로 갈 수 있기 때문에 3번 정점을 거쳐서 4번 정점으로 갈 때의 최단 거리는 3번 정점까지의 거리와 간선의 가중치를 합쳐 $2+2=4$이 됩니다. 이 값이 $d$ 테이블에 저장된 값보다 작을 경우 최단 거리 테이블에 쓰고 힙에 삽입을 해줍니다. 기존에는 5가 저장되어 있었으므로 4로 갱신을 해주면서 힙에 삽입합니다.
힙에 4번 정점에 대한 원소가 2개 들어있습니다. 이게 과연 올바르게 흘러가는건지 좀 의아할 수도 있습니다. 하지만 괜찮습니다. 정상입니다.

모든 처리가 끝났으니 (2, 3) 원소를 제거합니다.
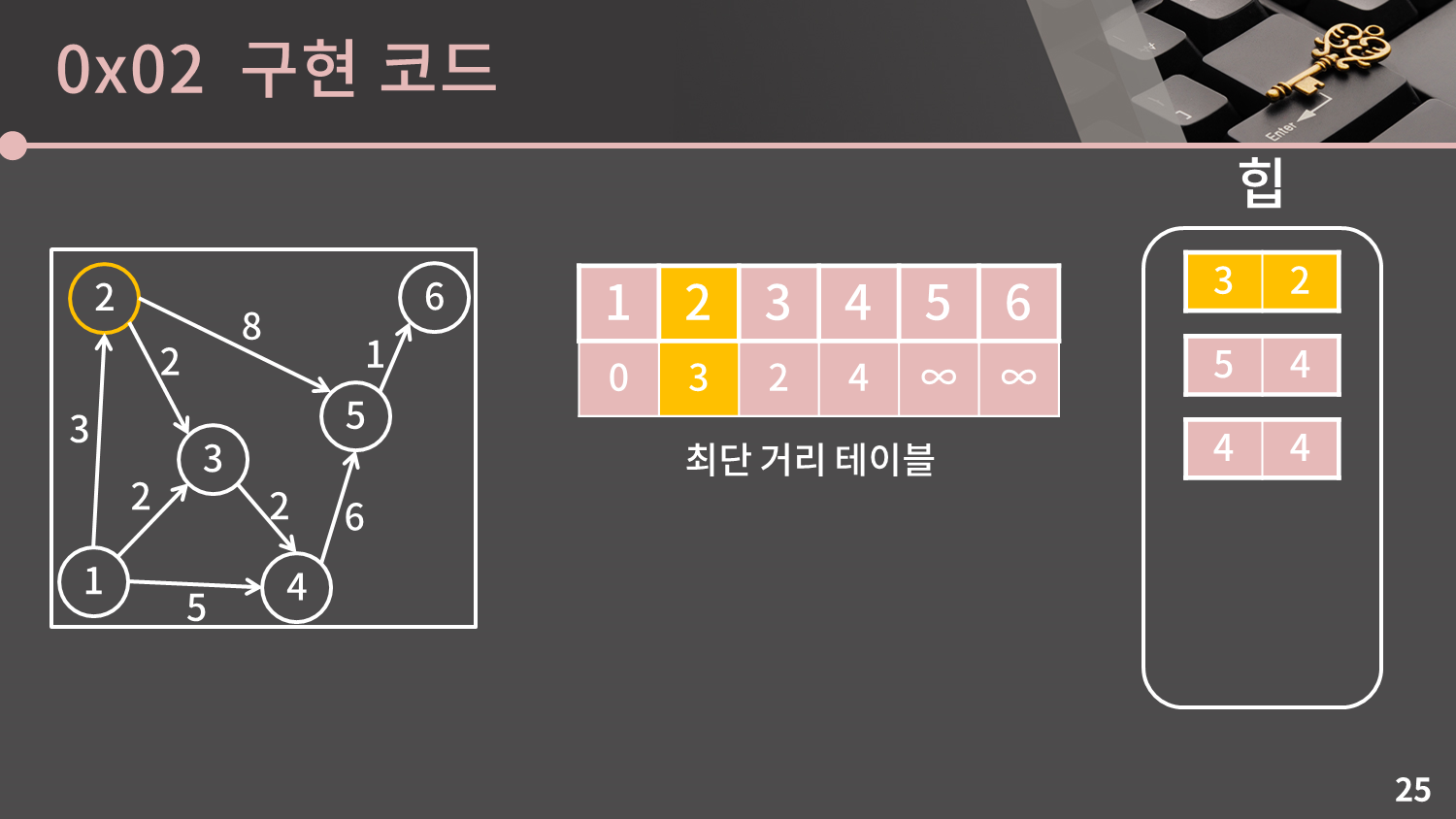
힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (3, 2)이 선택될 것입니다. 우선 $d[2] = 3$가 맞는지 확인합니다. 일치하므로 과정을 이어갑니다.

일단 시작점과 2번 정점의 거리는 3이고, 2번 정점에서 3, 5번 정점으로 갈 수 있기 때문에 2번 정점을 거쳐서 3, 5번 정점으로 갈 때의 최단 거리는 2번 정점까지의 거리와 간선의 가중치를 합쳐 각각 $3+2=5$, $3+8=11$이 됩니다. 이 값이 $d$ 테이블에 저장된 값보다 작을 경우 최단 거리 테이블에 쓰고 힙에 삽입을 해줍니다. 우선 3번 정점의 경우 기존의 값이 더 작으므로 아무 일도 일어나지 않습니다. 5번 정점의 경우 기존에는 ∞이 저장되어 있었으므로 이를 11로 갱신을 해주면서 힙에 삽입합니다.
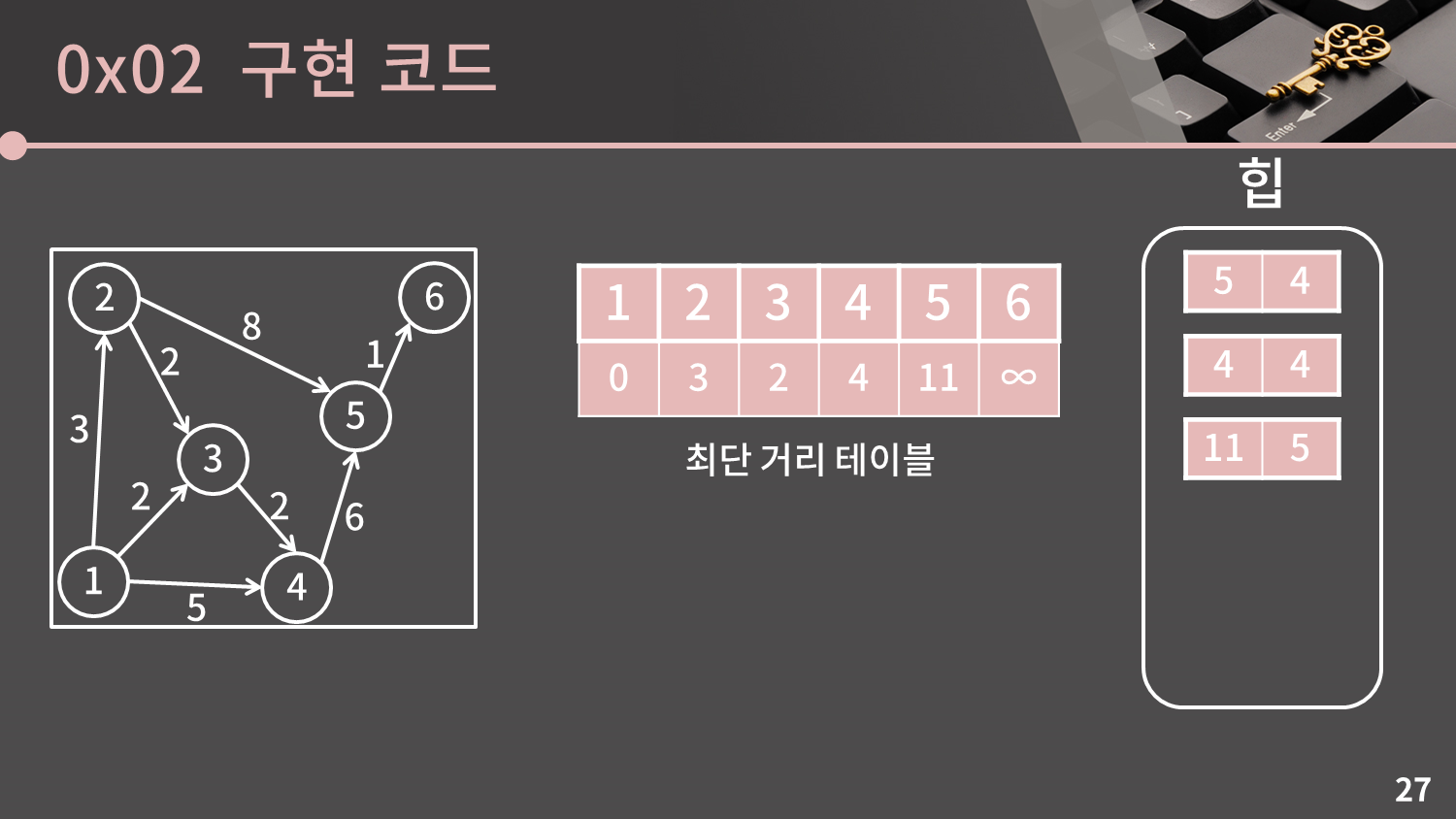
모든 처리가 끝났으니 (3, 2) 원소를 제거합니다.

힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (4, 4)이 선택될 것입니다. 우선 $d[4] = 4$가 맞는지 확인합니다. 일치하므로 과정을 이어갑니다.

일단 시작점과 4번 정점의 거리는 5이고, 4번 정점에서 5번 정점으로 갈 수 있기 때문에 4번 정점을 거쳐서 5번 정점으로 갈 때의 최단 거리는 4번 정점까지의 거리와 간선의 가중치를 합쳐 $4+6=10$이 됩니다. 이 값이 $d$ 테이블에 저장된 값보다 작을 경우 최단 거리 테이블에 쓰고 힙에 삽입을 해줍니다. 기존에는 11이 저장되어 있었으므로 4로 갱신을 해주면서 힙에 삽입합니다.
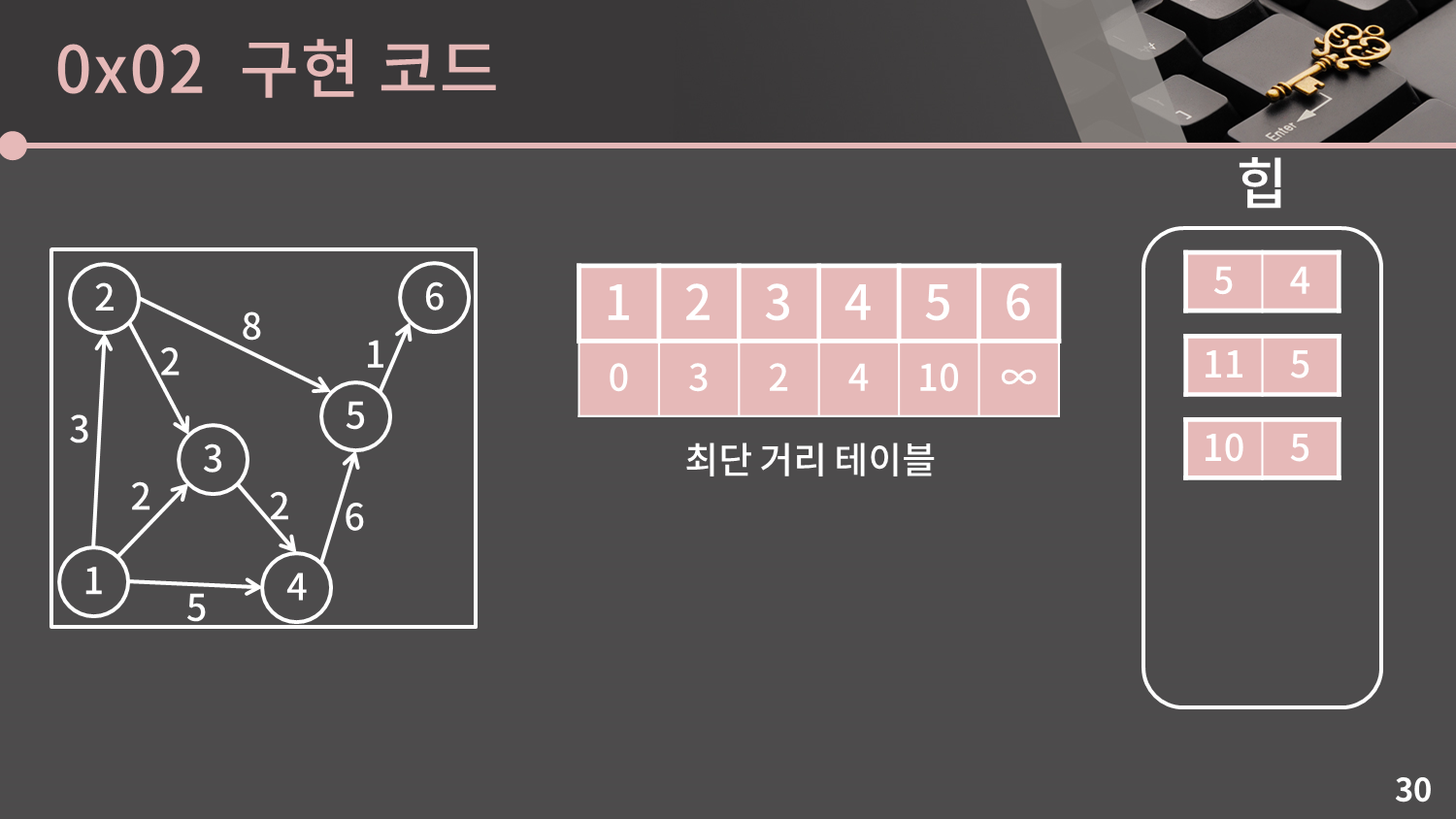
모든 처리가 끝났으니 (4, 4) 원소를 제거합니다.

힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (5, 4)이 선택될 것입니다. 우선 $d[4] = 5$가 맞는지 확인합니다. 최단 거리 테이블을 확인해보면 $d[4] = 4$이므로 해당 원소는 잘못된 원소입니다. 구체적으로 말해서 맨 처음에는 1에서 바로 4에게 가는 길이 5의 경로를 담고 있었지만 1->3->4로 가는 더 짧은 거리가 나왔기 때문에 쓸모가 없어진 원소입니다.

해당 원소는 쓸모가 없으므로 아무 처리도 하지 않고 (5, 4) 원소를 제거합니다.

힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (10, 5)가 선택될 것입니다. 우선 $d[5] = 10$이 맞는지 확인합니다. 일치하므로 과정을 이어갑니다.

일단 시작점과 5번 정점의 거리는 10이고, 5번 정점에서 6번 정점으로 갈 수 있기 때문에 5번 정점을 거쳐서 6번 정점으로 갈 때의 최단 거리는 5번 정점까지의 거리와 간선의 가중치를 합쳐 $10+1=11$이 됩니다. 이 값이 $d$ 테이블에 저장된 값보다 작을 경우 최단 거리 테이블에 쓰고 힙에 삽입을 해줍니다. 기존에는 ∞이 저장되어 있었으므로 11로 갱신을 해주면서 힙에 삽입합니다.

모든 처리가 끝났으니 (10, 5) 원소를 제거합니다.

힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙의 두 원소는 거리가 동일해 어느 것을 택해도 상관이 없는데 임의로 (11, 5)를 선택하겠습니다. 우선 $d[5] = 11$가 맞는지 확인합니다. 최단 거리 테이블을 확인해보면 $d[5] = 10$이므로 해당 원소는 잘못된 원소입니다.

해당 원소는 쓸모가 없으므로 아무 처리도 하지 않고 (11, 5) 원소를 제거합니다.

힙이 비어있지 않으므로 힙에서 가장 거리가 작은 원소를 선택합니다. 지금 힙에서는 (11, 6)가 선택될 것입니다. 우선 $d[6] = 11$이 맞는지 확인합니다. 일치하므로 과정을 이어갑니다.

6에서 다른 정점으로 가는 간선은 존재하지 않으므로 따로 처리를 해줄 것이 없습니다.

모든 처리가 끝났으니 (11, 6) 원소를 제거합니다.
힙이 비었으므로 다익스트라 알고리즘이 종료됩니다. 최단 거리가 잘 들어가있음을 확인 가능합니다.
과정을 한 번 살펴보았습니다. 각 간선 당 최대 1개의 원소가 힙에 들어갈 수 있게 되어 힙에서의 삽입과 삭제가 최대 $E$번씩 발생합니다. 그러므로 시간복잡도는 $O(ElgE)$입니다.
힙을 이용한 다익스트라 알고리즘을 직접 구현할 수 있겠나요? 쉽진 않지만 좋은 훈련이 될 것입니다. 직접 시도해보시고 다음 슬라이드로 넘어와주세요.
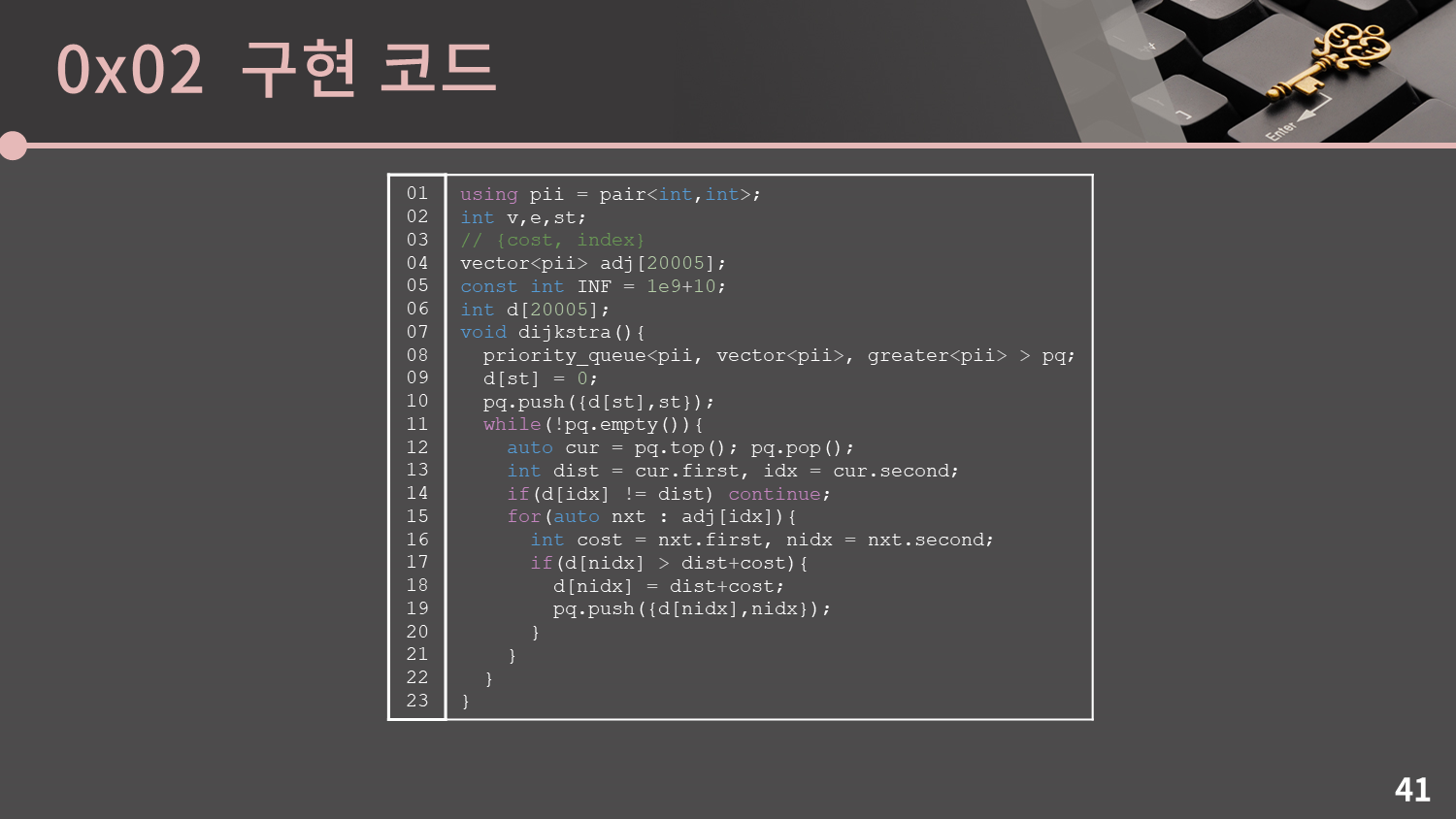
이것이 다익스트라 알고리즘의 코드입니다. $st$는 시작 정점의 번호를 의미합니다.
프림 알고리즘을 소개할 때 최초로 소개했던 것과 같이 adj는 vector배열이 아니고 vector<pair<int,int> > 배열입니다. 정점 번호 뿐만 아니라 연결하는 간선의 값도 알고 있어야 하기 때문입니다.
INF값은 실제로 가능한 거리보다 더 큰 값이어야 합니다. 만약 주어진 제한조건이 정점 2만개, 간선의 비용은 최대 10만이라고 하면 거리의 최댓값은 2만에 10만을 곱한 $2 \times 10^9$이 됩니다. 이럴 때에는 INF값을 늘려줄 필요가 있습니다. 그리고 overflow에 주의하세요.
8번 줄에서 priority_queue로 pq를 선언한다면 pq는 max heap, 즉 가장 큰 값의 확인/삭제가 가능한 힙이 됩니다. 그러므로 functional 헤더에 있는 greater를 이용해 해당 힙을 min heap으로 만들어주었습니다.
시뮬레이션에서 본 것과 같이 우선 힙에 {0, st}를 대입합니다. 이후 힙에 원소가 없을 때 까지 원소를 꺼내고, 인접한 정점들에 대해 $d$ 값을 갱신하고 힙에 넣는 작업을 반복합니다. 14번 줄의 처리를 통해 잘못된 원소를 걸러내야 함에 주의하세요.
다익스트라 알고리즘을 잘못 짜는 대표적인 예시로 14번 줄의 처리를 빼먹거나, priority_queue에서 index와 cost를 반대로 넣어 최소 원소를 꺼내지 않고 이상한 원소를 꺼내는 것 등이 있습니다. 지금 이 코드를 보면서 한 두 번 대충 짜보거나 눈으로만 훑고 지나가면 실제로 짤 때 끝없이 많은 실수를 하게 됩니다. 기본적인 틀을 머리에 넣어두고, 아무 것도 보지 않은 채로 직접 완벽하게 짤 수 있을 때 까지 계속 연습해주세요.

BOJ 1753번: 최단경로 문제를 풀어봅시다. 다음 슬라이드에 정답 코드가 나옵니다.

아까의 다익스트라 알고리즘 코드를 적절하게 끼워넣으면 됩니다. 크게 달라진 점은 없습니다.
문제의 조건에서 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수 있다고 했는데도 그에 대한 처리가 없는 것을 볼 수 있는데, 별도로 처리를 하지 않아도 어차피 다익스트라 알고리즘 과정을 진행하다보면 비용이 더 큰 간선은 알아서 반영이 되지 않기 때문입니다. 정답 코드를 확인해보세요.

다익스트라 알고리즘에서도 경로 복원의 필요성이 있습니다. 저희는 현재 최단 거리만 알고 있지 실제 어떤 경로로 가야하는지는 모르니까요. 플로이드 알고리즘에서 경로 복원을 한 번 했으니 다익스트라 알고리즘에서는 어떻게 하면 좋을지 한 번 고민을 해보세요. 충분히 혼자 힘으로 떠올릴 수 있습니다.

방법은 플로이드 알고리즘에서 한 것과 크게 다르지 않습니다. 최단 거리 테이블이 갱신될 때 어디를 거쳐가면 되는지를 남기면 됩니다.
이 테이블은 시작점에서 나에게로 올 때 직전에 어디를 방문했는지 기록하는 테이블이므로 $pre$ 테이블이라고 쓰겠습니다.

다익스트라 알고리즘의 진행 과정은 충분히 익숙해졌을거라 믿고 최단 거리 테이블이 갱신됨에 따라 $pre$ 테이블의 변화만 찝어서 보겠습니다.
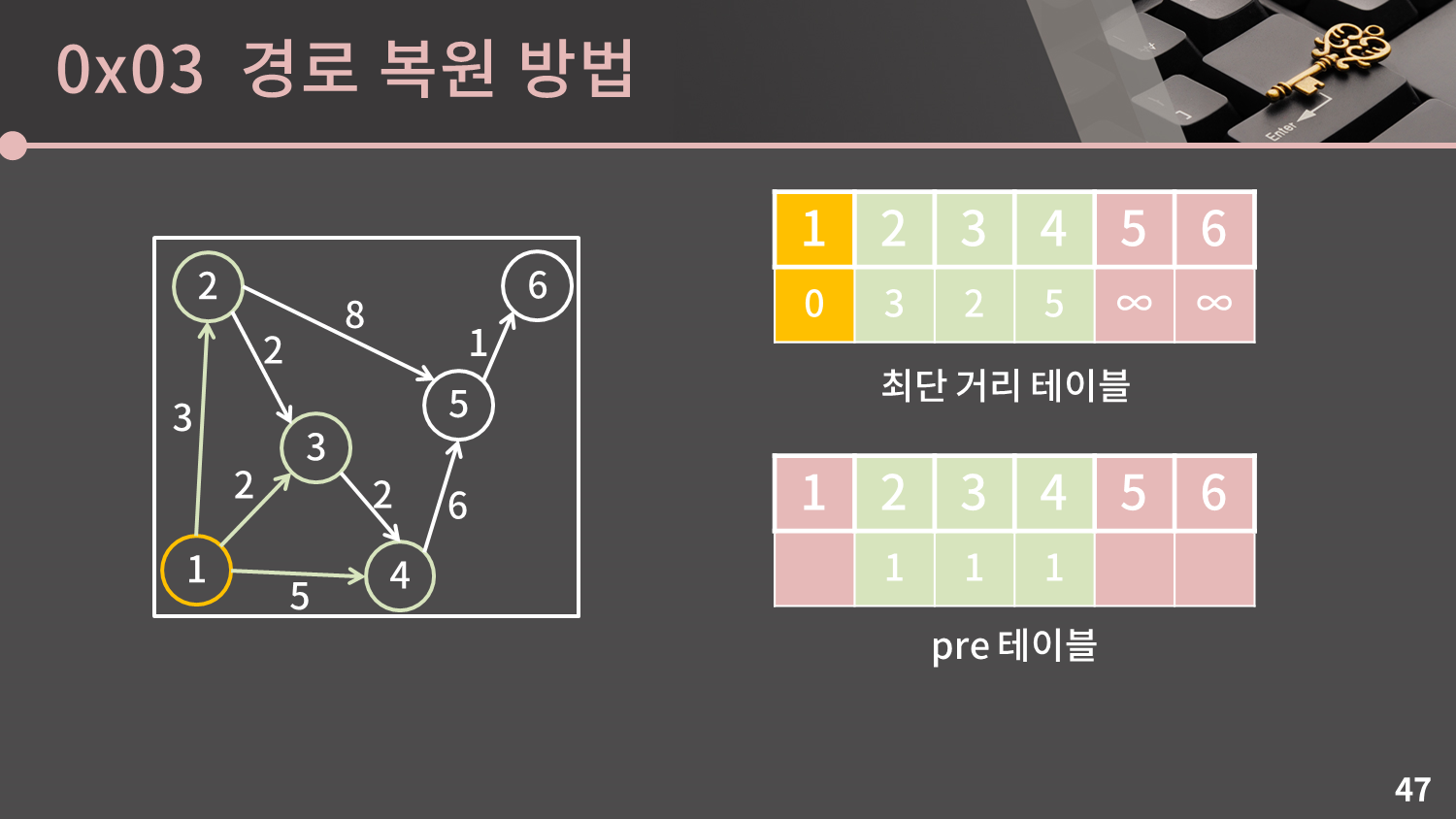
1번 정점이 선택되어 2, 3, 4번 정점의 최단 거리 값이 변경될 때 $pre[2], pre[3], pre[4]$에는 1이 기록됩니다.

3번 정점이 선택되어 4번 정점의 최단 거리 값이 변경될 때 $pre[4]$에는 3이 기록됩니다.

2번 정점이 선택되어 5번 정점의 최단 거리 값이 변경될 때 $pre[5]$에는 2가 기록됩니다.

4번 정점이 선택되어 5번 정점의 최단 거리 값이 변경될 때 $pre[5]$에는 4가 기록됩니다.

5번 정점이 선택되어 6번 정점의 최단 거리 값이 변경될 때 $pre[6]$에는 5가 기록됩니다.

이렇게 $pre$ 테이블을 다 채운 뒤에는 시작점에서 $t$로 가는 경로를 복원하는 것을 어렵지 않게 구현할 수 있을 것입니다. $cur$ 변수가 $t$에서 시작해 시작점까지 $pre$를 계속 타고 가며 $path$ vector에 계속 push_back을 해주다가 마지막에 reverse를 하면 됩니다.
결과가 깔끔하게 들어있는 vector를 만들고 싶어 reverse를 사용하긴 했지만 단순히 출력만 하면 되는 상황이면 굳이 reverse를 할 필요 없이 역으로 출력을 해도 상관 없습니다.

경로 복원과 관련해 풀어 볼 연습 문제는 BOJ 11779번: 최소비용 구하기 2 문제입니다. 이 문제에서는 최단 거리와 더불어 경로까지 출력할 것을 요구합니다.
이전 문제에 썼던 코드에서 $pre$ 배열을 갱신하고, 이후 $pre$ 배열을 이용해 경로를 출력할 수 있도록 수정을 하면 됩니다. 주어지는 입력의 형식이 이전 문제와 약간 다르다는 점에 유의하세요. 직접 한 번 해보세요. 다음 슬라이드에는 정답 코드가 나와있습니다.

대부분의 코드가 유사하니 $pre$배열과 관련한 부분만 짚고 넘어가겠습니다. 입력을 처리하는 22번째 줄 까지는 특이한 것이 없습니다. while문을 돌면서 32번째 줄의 갱신이 일어날 때, 35번째 줄과 같이 pre 값을 넣어줍니다.
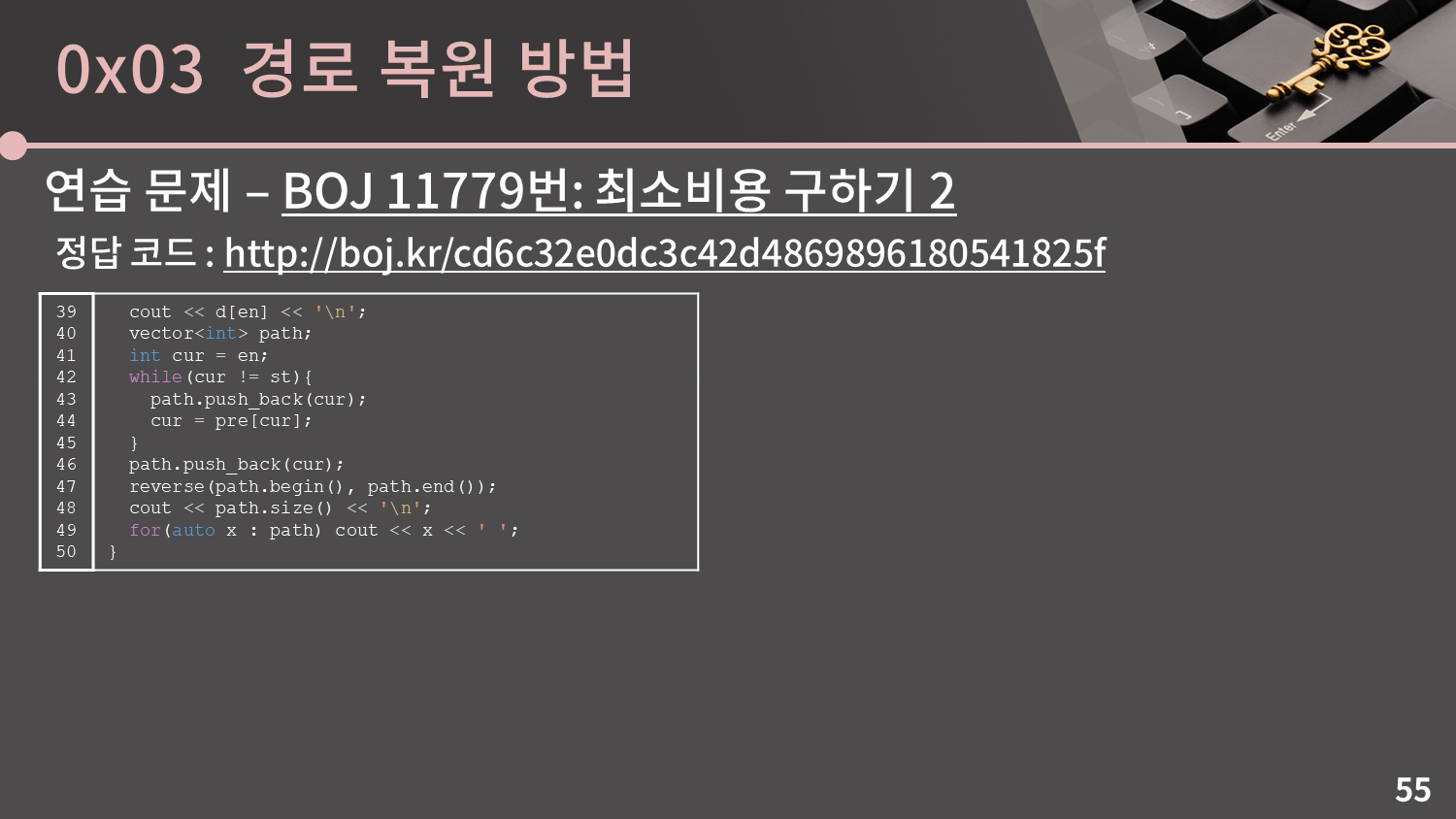
이후에는 $d[en]$ 값을 출력하고, 경로 복원을 해주면 됩니다. 정답 코드를 확인해보세요.
이 문제를 통해 배울 수 있는 또 한가지 정보가 있습니다. 하나의 시작점에서 다른 모든 정점까지의 거리나 경로를 구하는 것이 아니라 하나의 시작점에서 하나의 끝점까지의 거리나 경로를 구하는 상황이라고 하더라도 다익스트라 알고리즘을 쓰면 된다는 사실입니다.

이번 강의를 통해 다익스트라 알고리즘을 익혔습니다. 다익스트라 알고리즘은 무방향 혹은 방향 그래프에서 하나의 시작점로부터 다른 모든 정점 까지의 최단 거리를 $O(ElgE)$에 구해주는 알고리즘입니다. 단, 음수의 가중치를 가지는 간선이 포함되어 있을 때에는 사용할 수 없습니다. 응용문제가 다양하고 면접에서도 물어보기 좋은 알고리즘이니 필히 마스터하시길 바랍니다.
약 1년 전에 시작했는데 이제야 강좌가 완결났네요. 늘 마음의 빚이었는데 끝나서 정말 기쁩니다. 지금까지의 강의를 충실히 따라오시면서 문제를 꾸준하게 푸셨다면 앞으로 코딩테스트에서 애를 먹을 일은 절대 없다고 장담할 수 있습니다.
코딩테스트 공부를 하는 과정이 재미 없었다면 딱 여기까지만 한 후에 AI, 블록체인, 프론트엔드, 기타 개발, 혹은 CTF 등과 같이 본인이 하고 싶은 일을 찾아가시면 되고, 이 과정에서 즐거움을 많이 느껴 알고리즘 공부를 계속 하고 싶다면 이번 강의에서는 다루지 않은 parametric search, Meet In The Middle, LCA, Trie, Network Flow, Segment Tree 등과 같은 것들을 하나씩 익혀나가며 페이스북 해커컵, 구글 코드잼과 같은 대회의 길로 접어드는 것도 괜찮을 것 같습니다.
만약 삼성 B형(=Professional 등급)을 준비하고 계신다면 힙, 해쉬, 트라이, 링크드 리스트, 벡터 등을 맨 바닥에서 짤 수 있어야 합니다. 언젠가 심화 알고리즘과 더불어 기본 자료구조를 STL 없이 짜는 방법에 대한 강의를 만들고 싶습니다만 기약은 없습니다. 심화 알고리즘은 라이님의 블로그를 참고하시면 되겠습니다.
긴 시간동안 응원해주신 모든 분들께 감사합니다. 제 강의가 큰 도움이 되었으면 좋겠습니다!
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x02강 - 기초 코드 작성 요령 II (53) | 2020.02.16 |
|---|---|
| [실전 알고리즘] 0x01강 - 기초 코드 작성 요령 I (80) | 2020.02.12 |
| [실전 알고리즘] 0x00강 - 오리엔테이션 (55) | 2020.02.10 |
| [실전 알고리즘] 0x13강 - 플로이드 알고리즘_구버전 (9) | 2020.01.28 |
| [실전 알고리즘] 0x12강 - 최소 신장 트리_구버전 (18) | 2020.01.27 |
| [실전 알고리즘] 0x11강 - 위상 정렬_구버전 (13) | 2020.01.17 |