문제 링크
https://programmers.co.kr/learn/courses/30/lessons/81303
예상 난이도
S1 - G4
알고리즘 분류
연결 리스트 or 이진 검색 트리(or 세그먼트 트리)
풀이

제 강의를 통해 연결 리스트를 익히셨다면 문제를 읽었을 때 연결 리스트가 필요하다는걸 떠올릴 수 있습니다.(BOJ 1406, BOJ 5397 참고)
가장 최근에 삭제된 행을 확인하는 작업과 관련해서는 스택이 쓰입니다. 그런데 연결 리스트로 U, D, C 명령은 쉽게 처리가 가능한 반면 Z 명령은 그렇지가 않습니다. Z 명령을 처리하기 위해서는 삭제할 때 어떤 정보를 저장하고 있어야할지 생각해봅시다. 그림의 별이 현재 선택된 행을 의미한다고 치고 여기서 C 명령을 수행해봅시다.

나중에 복구를 하려면 2행이 제거되었다는 정보는 필요할테니 스택에 2를 넣겠습니다. 다시 C 명령을 수행해봅시다.

다음으로 U 2를 수행하겠습니다.


이 상황에서 Z를 수행한다고 하면, 제거된 3행을 복구시켜야 한다는건 알 수 있지만 어디에 복구를 해야할지 아무 것도 할 수 있는게 없습니다. 저희는 지금 그림으로 한 눈에 보고 있으니 3행을 4번 앞에 붙이면 된다는걸 알지만 구현을 하는 상황에서는 좀 막막합니다.
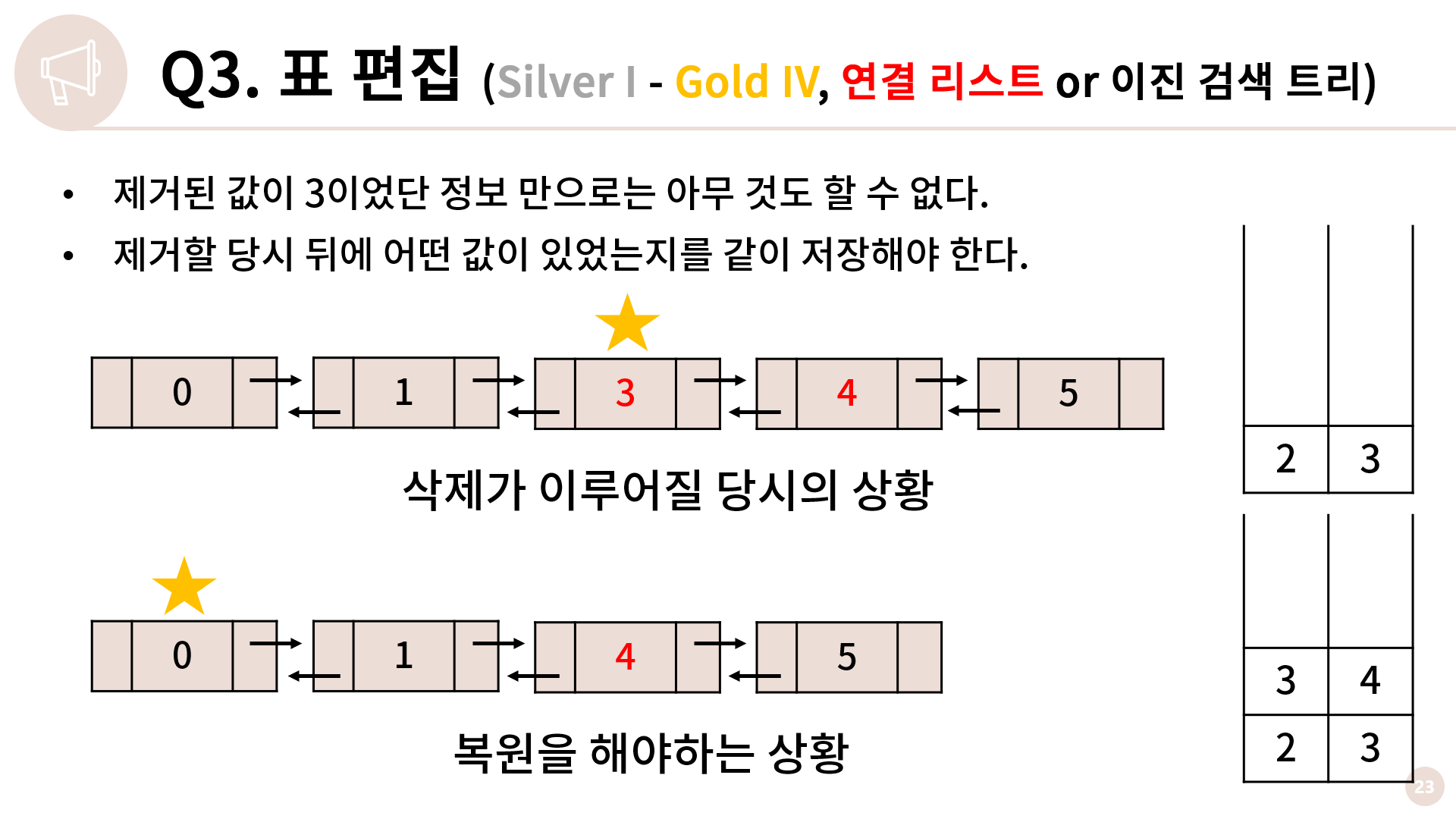
그렇기 때문에 이와 같이 C 명령을 수행할 때, 뒤에 어떤 값이 있었는지를 같이 스택에 저장해야 복구할 행을 어떤 행 앞에 붙여야 하는지 알 수 있습니다.

그런데 문제가 1개 더 있는데, 스택에 4를 같이 넣어서 4의 앞에 3을 추가하면 된다는건 알 수 있지만 연결 리스트의 특성상 현재 4가 어디에 있는지를 알 방법이 없습니다.

이 문제를 해결하기 위해 별도로 its[..] 배열을 둬서 i가 들어있는 원소의 위치를 나타내도록 했습니다. 자세한건 코드를 참고하세요.

제일 마지막 원소인 n-1행의 경우에는 뒤에 원소가 없어서 애매해질 수 있으니, 예외처리를 덜 번거롭게 하기 위해서 리스트의 제일 뒤에 원소 n을 임의로 추가했습니다.
C++에서는 STL의 list를 사용하면 되지만 Java는 LinkedList 라이브러리에서 iterator의 이동이 자유롭지 않고, Python은 아예 연결 리스트 라이브러리가 없기 때문에 두 언어에서는 직접 연결 리스트를 구현해야 합니다. 구조체를 사용하는 정석 구현을 어디선가 가져와서 써도 되지만 저는 그냥 야매 연결 리스트를 이용해서 구현했습니다.
참고로 Java의 경우 정답자들의 코드를 보니 일부 코드가 O(n+1000000)이 아닌 O(n2)에 동작함에도 불구하고 정답 처리가 되는 경우가 있었습니다(구체적으로 해당 방법을 설명하면 연결 리스트를 사용하지 않고 모든 연산을 O(1)에 수행한 후 삭제된 행의 위치만을 기억해두었다가 맨 마지막에 지운 횟수만큼 stringbuilder의 insert 함수를 적용하는 방식인데, 이 방식의 시간복잡도는 최악의 경우 O(nq)입니다. q는 cmd의 원소 개수. 즉 현재는 문제의 데이터가 약해서 통과되는거지 원래라면 시간초과가 발생해야 합니다). 아마 본인이 이 문제를 맞췄다고 생각하는 분이면 이 풀이를 읽고 있지 않을 것 같긴 하지만, 자신이 작성한 코드의 시간복잡도를 유추하지 않은 채로 작성했는데 통과가 되었을 경우 올바르지 않은 시간복잡도로 통과한건 아닌지 시간복잡도를 따져서 잘못된 지식을 익히고 가는 일이 없도록 합시다.
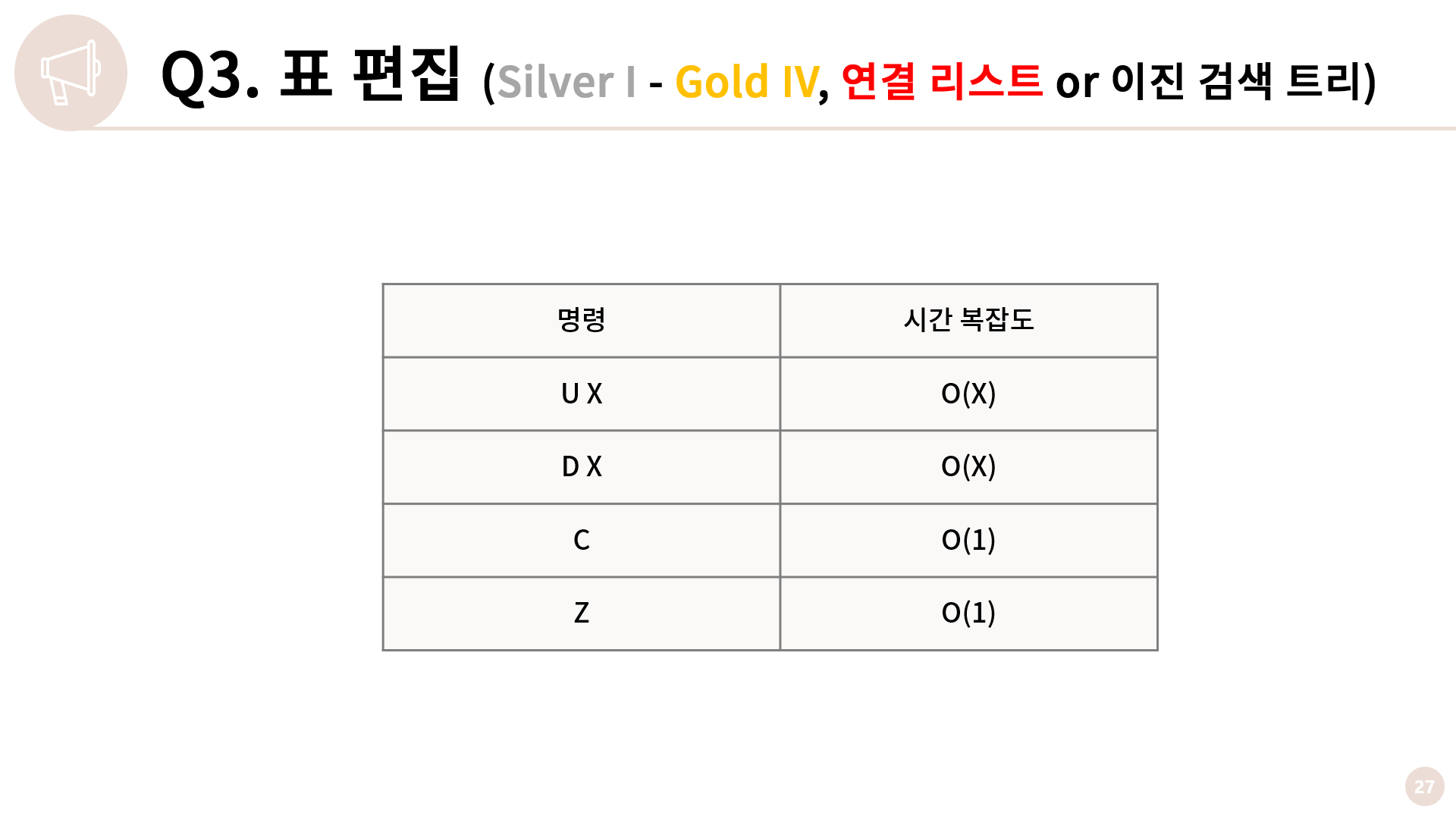
이렇게 연결 리스트를 사용한 풀이는 각 명령의 시간복잡도가 위와 같습니다. U, D는 이동 횟수에 비례한 시간이 걸리지만 이동의 총 합이 1,000,000 이하라는 단서가 있어서 괜찮습니다. 여기까지가 연결 리스트를 이용하는 첫 번째 풀이입니다.

일반적인 연결 리스트에서는 통하지 않지만 이 문제에 한해서 사용 가능한 두 번째 풀이가 있습니다. 만약 직접 연결 리스트를 구현해본 경험이 없다면 이 풀이는 이해가 어려울 수 있습니다.
문제의 상황을 잘 관찰해보면 이 문제에서는 원소가 0에서 n-1사이로 제한되고, 삭제에 대한 복구 이외에는 삽입이 없습니다. 이 관찰을 바탕으로 연결 리스트를 훨씬 더 간단하게 만들 수 있습니다.
저희는 연결 리스트에서 "주소" 혹은 "번지"라는 개념을 담아서 주소를 넘나드는 방식으로 구현을 하는데, 원소가 어차피 0에서 n-1로 제한되기 때문에 살짝 배열의 느낌을 담아서 각 원소의 주소를 고정시킵니다. 그러고 나면 pre, nxt에서 이전/다음 원소의 주소를 가지고 있는 대신 바로 이전/다음 원소의 값을 가지고 있으면 됩니다. 이렇게 했을 때 Z 명령이 아주 간단해지는데, Z 명령을 수행할 때 새 원소를 추가하는 대신 pre, nxt 값을 올바르게 고쳐 원소를 복구합니다.
글로 읽으면 살짝 헷갈릴 수 있는데 실제 명령을 수행하는 그림을 보면 이해가 갈 것 같습니다.
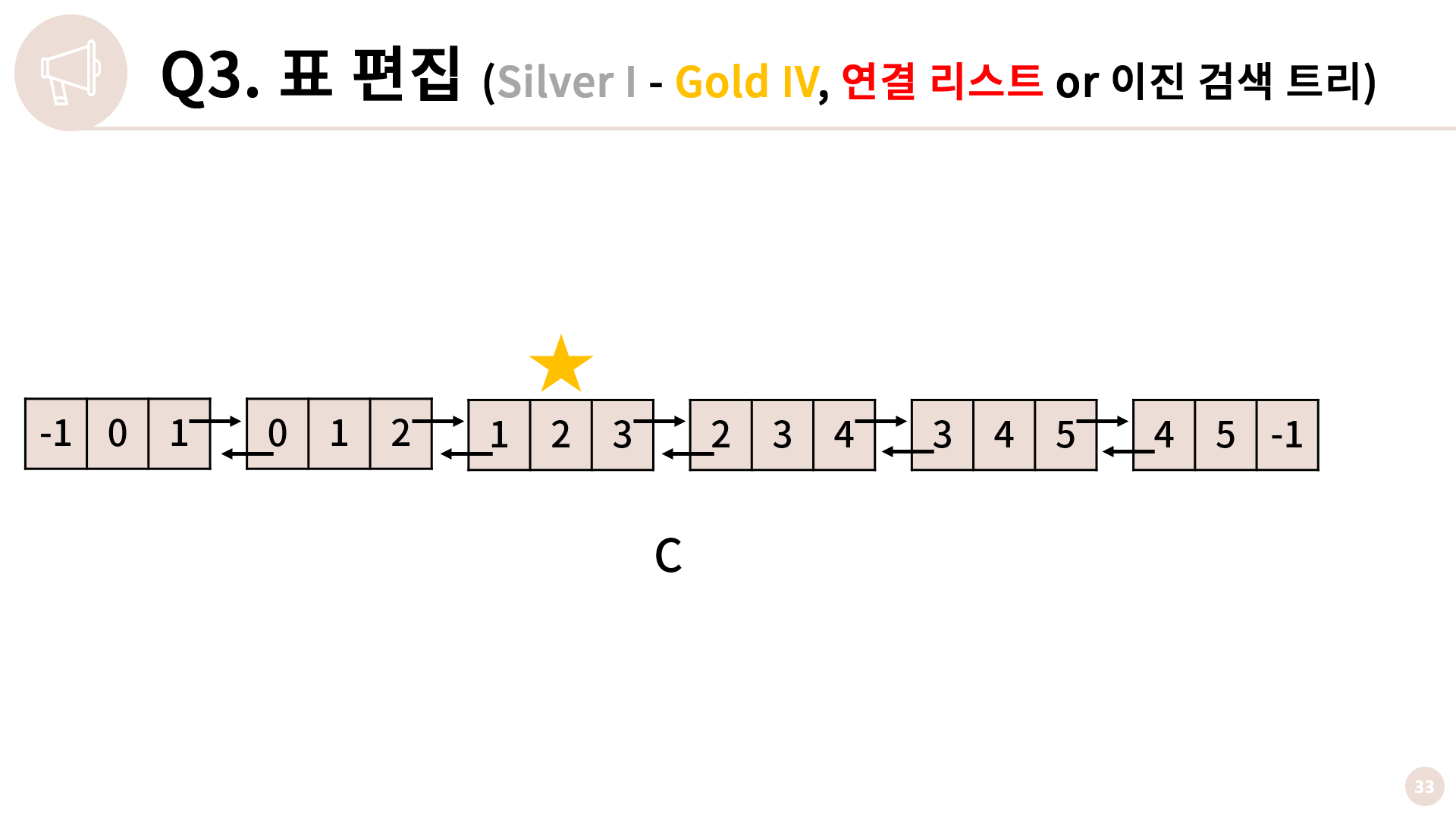
여기서 제거 명령을 수행해봅시다.

제거를 수행할 때 2행에 대응되는 pre, nxt는 바꿀 필요가 없고, nxt[1]과 pre[3]만 변경을 하면 됩니다.

그 다음 제거에서도 마찬가지로 pre[1]과 nxt[4]만 변경하면 됩니다.

U 2는 크게 어렵지 않습니다. 이제 사실상 핵심이라고 볼 수 있는 Z 명령을 어떻게 처리할 수 있을지 봅시다.

우선 스택을 보고 3번 행을 돌려야 한다는건 알 수 있습니다. 3번 행에 적힌 값들은 삭제 당시의 값이기 때문에 건드릴 필요가 없습니다. 그 다음으로 pre[3](= 1)을 확인해 nxt[1] = 3이 되도록 하고, nxt[3](= 4)를 확인해 pre[4] = 3이 되도록 하면 복구가 끝납니다.
이렇게 이 문제에서의 특수한 상황을 이용해 연결 리스트를 간단하게 구현하는게 두 번째 풀이입니다. STL을 가져다 쓰면 되는 C++입장에서는 첫 번째 풀이나 두 번째 풀이나 큰 차이가 없지만 Java, Python에서는 이 두 번째 풀이가 구현이 더 간단합니다.


그리고 세 번째 풀이는 이진 검색 트리를 이용하는 풀이입니다. 문제의 상황을 다르게 생각해보면 원소들을 정렬된 상태로 가지고 있다가 임의 위치에서 제거/삭제한다는 관점으로 볼 수도 있고, 이 상황은 이진 검색 트리로도 구현하기 아주 좋은 상황입니다. 또한 이진 검색 트리에서 iterator의 한 칸 이동은 O(lg N)이기 때문에 U, D 연산 또한 별 문제 없이 수행 가능합니다.
단 이 풀이는 STL에 set이 있는 C++에서만 활용 가능합니다. Java는 TreeMap 라이브러리가 있긴 하지만 iterator의 이동이 자유롭지 않고, Python은 이진 검색 트리 라이브러리가 없습니다. 이진 검색 트리를 직접 구현하면 되긴 한다만 그건 사실상 불가능에 가깝습니다. 이진 검색 트리로 풀면 모든 연산이 연결 리스트보다 lgN만큼 더 오래 걸리기 때문에 그다지 좋은 방법이라고 볼 수는 없지만, 이진 검색 트리에서도 iterator를 옮길 수 있다는 것 정도만 익혀가시면 되겠습니다.
Java에서 최종적으로 답을 모을 때 StringBuilder를 사용하는 대신 String에서 += 을 n번 사용할 경우 O(n2)이 되어 시간초과가 날 수 있음을 주의해야 합니다.
관련 강의
0x04강 - 연결 리스트
0x16강 - 이진 검색 트리
'알고리즘 > Programmers' 카테고리의 다른 글
| [2022 KAKAO Blind Recruitment] Q1. 신고 결과 받기 (C++, Python, Java) (0) | 2022.01.17 |
|---|---|
| [2021 카카오 채용연계형 인턴십] Q5. 시험장 나누기 (C++, Python, Java) (0) | 2021.08.16 |
| [2021 카카오 채용연계형 인턴십] Q4. 미로 탈출 (C++, Python, Java) (3) | 2021.08.16 |
| [2021 카카오 채용연계형 인턴십] Q2. 거리두기 확인하기 (C++, Python, Java) (2) | 2021.08.16 |
| [2021 카카오 채용연계형 인턴십] Q1. 숫자 문자열과 영단어 (C++, Python, Java) (0) | 2021.08.16 |
| [2021 KAKAO Blind Recruitment] Q7. 매출 하락 최소화 (C++, Python, Java) (0) | 2021.08.15 |