문제 링크
https://programmers.co.kr/learn/courses/30/lessons/81305
예상 난이도
P5
알고리즘 분류
트리, 그리디, Parametric Search
풀이

보통 코딩테스트 문제에서 5분 이상 풀이를 못잡고 있는 일이 잘 없는데 이 문제는 처음 접했을 당시 꽤 헤맸습니다. 아무튼 문제를 봤을 때 뭔가 느낌적으로 최소화된 최대 그룹의 인원을 직접 구하는 최적화 문제는 해결 방법이 아예 감이 안오지만 각 그룹의 수를 x명으로 제한할 때 그룹의 수가 k개 이하인지를 판단하는 결정 문제는 어떻게 해결이 가능할 것 같다는 생각이 듭니다. 즉 Parametric Search입니다. 왜 그런 생각이 드냐고 했을 때 뭐라고 좀 설득력있게 말을 할 방법이 안떠오르긴 하는데, 그냥 Parametric Search 문제를 많이 풀다보니 얻게된 능력이라고 이해해주세요.
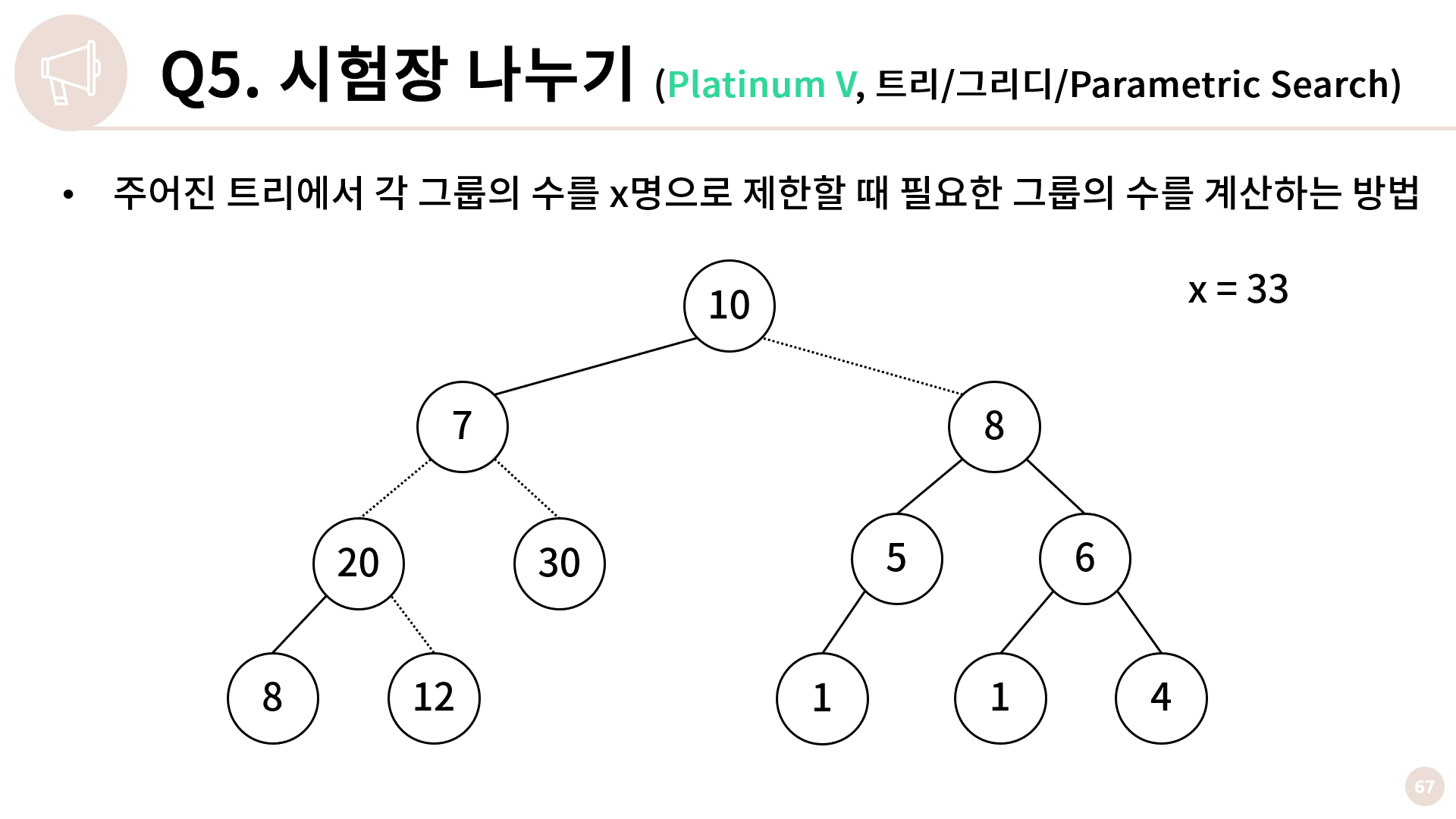
아무튼 우리는 결정 문제를 해결하기 위해 주어진 트리에서 각 그룹의 수를 x명으로 제한할 때 필요한 그룹의 수를 계산할 수 있어야 합니다.

각 그룹의 수를 x명으로 제한할 때 필요한 그룹의 수를 계산하기 위해서 그리디가 등장합니다. 저희는 리프에서부터 올라가면서 그룹의 정원이 차지 않을 때 까지 최대한 그룹 생성을 미루고 위로 올려보낼겁니다. x = 33일 때를 예로 들어 설명해볼테니 과정을 살펴봅시다.
먼저 크기가 8인 노드를 보면, 아직 그룹의 최대 크기 33에 도달하지 않았으니 위로 올려보냅니다.

크기가 12인 노드에 대해서도 마찬가지입니다.

크기가 20인 노드를 보면 왼쪽 자식에서 8이 넘어오고 오른쪽 자식에서 12가 넘어오는데, 20+8+12는 33보다 크기 때문에 감당할 수 없습니다. 그나마 다행인건 두 자식 중에서 하나는 감당이 가능합니다. 8을 가지고 올라가도 되고 12를 가지고 올라가도 되는데 둘 중 무엇을 가지고 올라가는게 좋을까요?

둘 중에서 작은걸 가지고 올라가는게 그룹의 수를 줄이는데 도움이 됩니다. 그렇기 때문에 오른쪽 자식은 혼자 그룹을 만들어 빠지게 하고 왼쪽 자식을 가져간 채로 28을 위로 올려보냅니다.
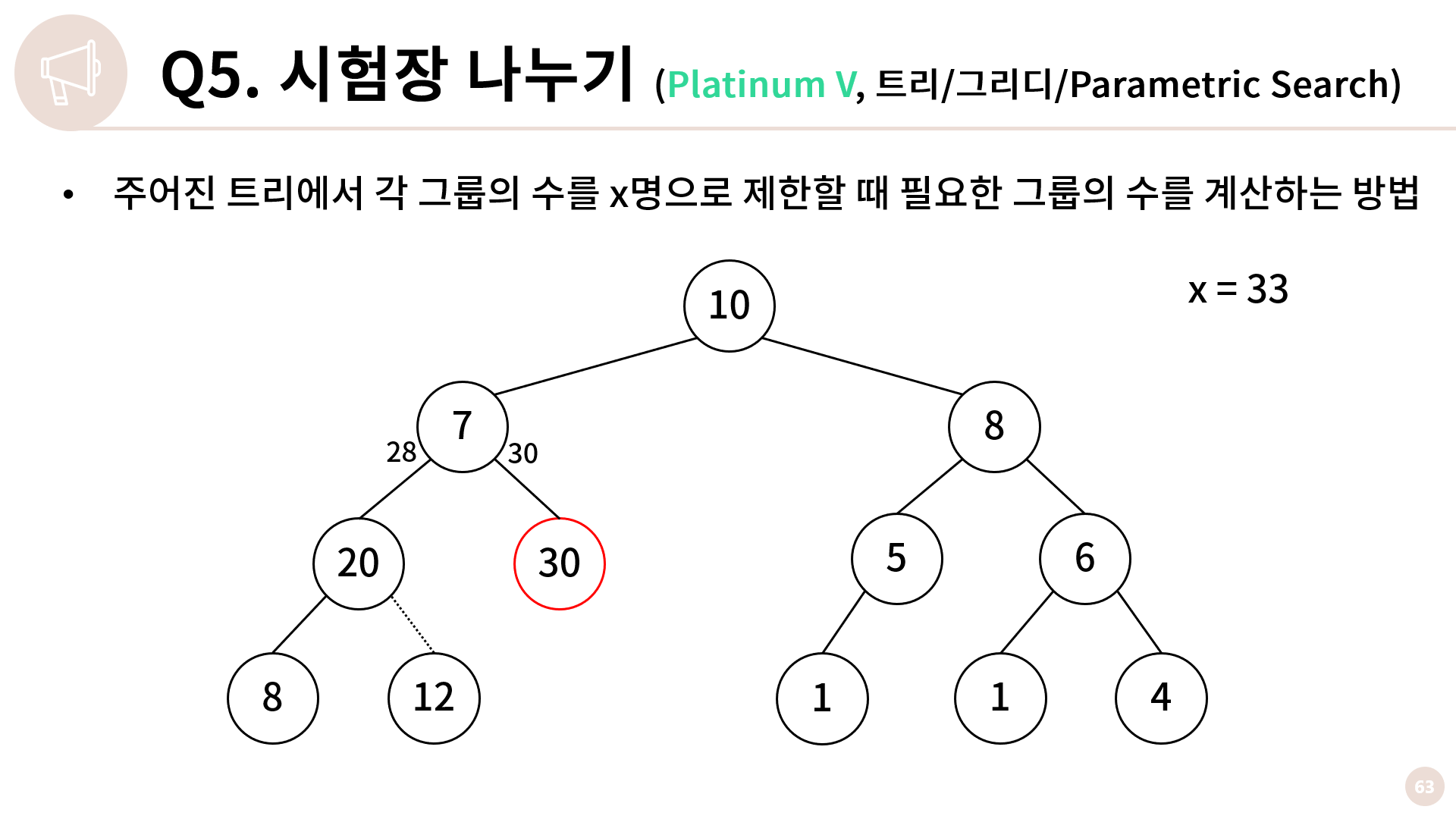
크기가 30인 노드는 그대로 30을 위로 올립니다.
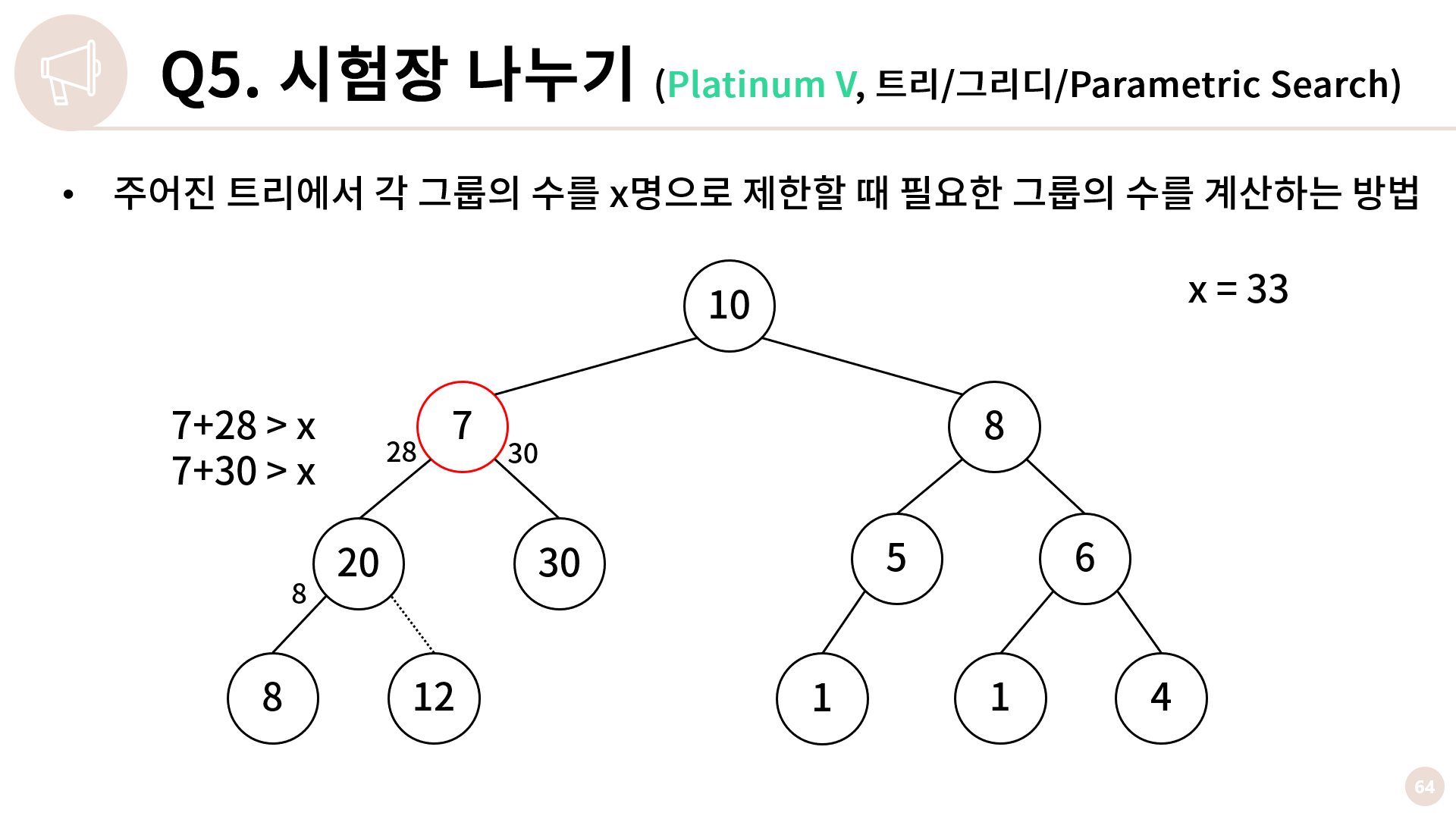
크기가 7인 노드는 왼쪽 자식도, 오른쪽 자식도 가지고 갈 수 없습니다.
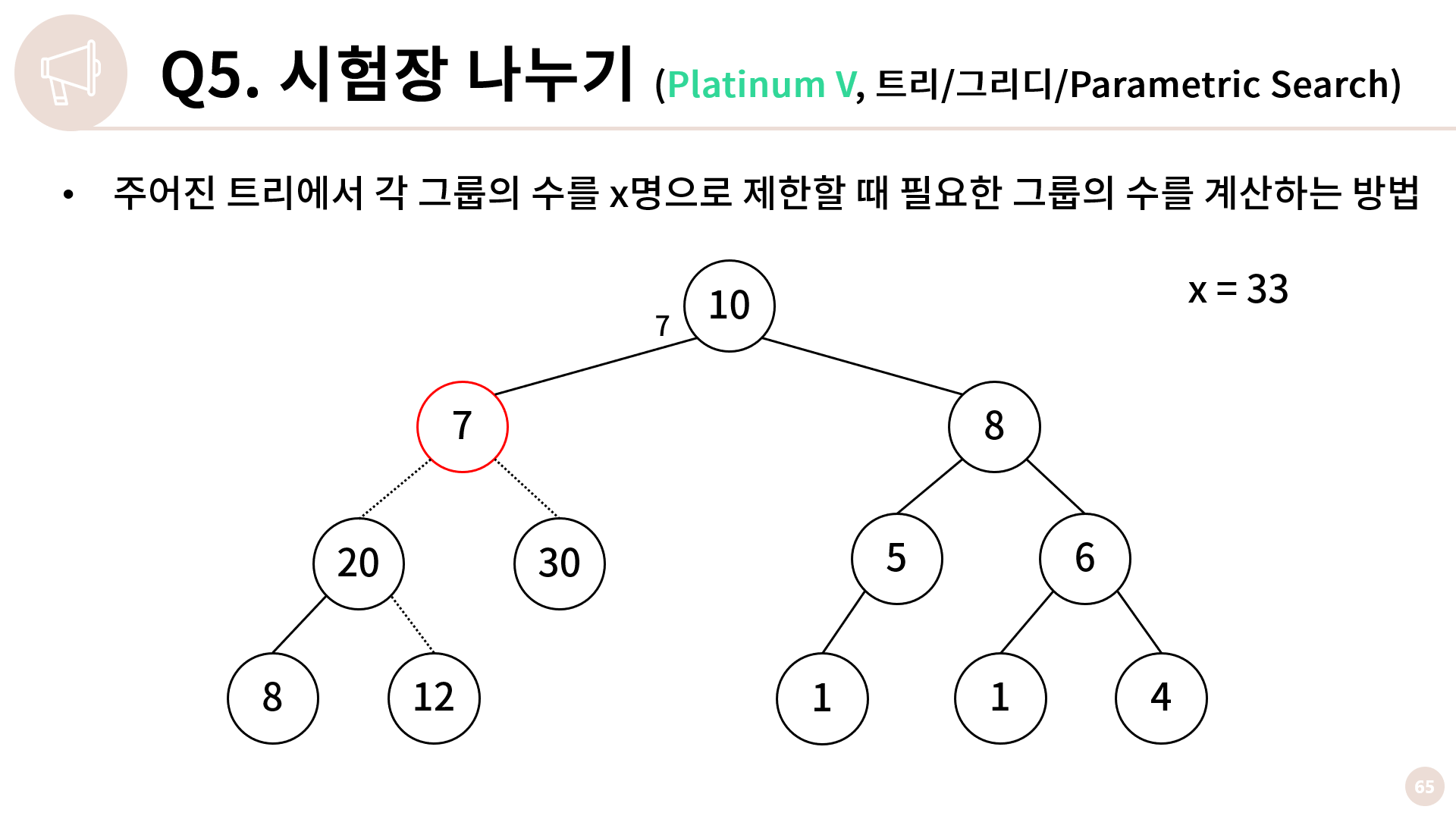
그래서 둘 다 끊어내고 7을 올려보냅니다.
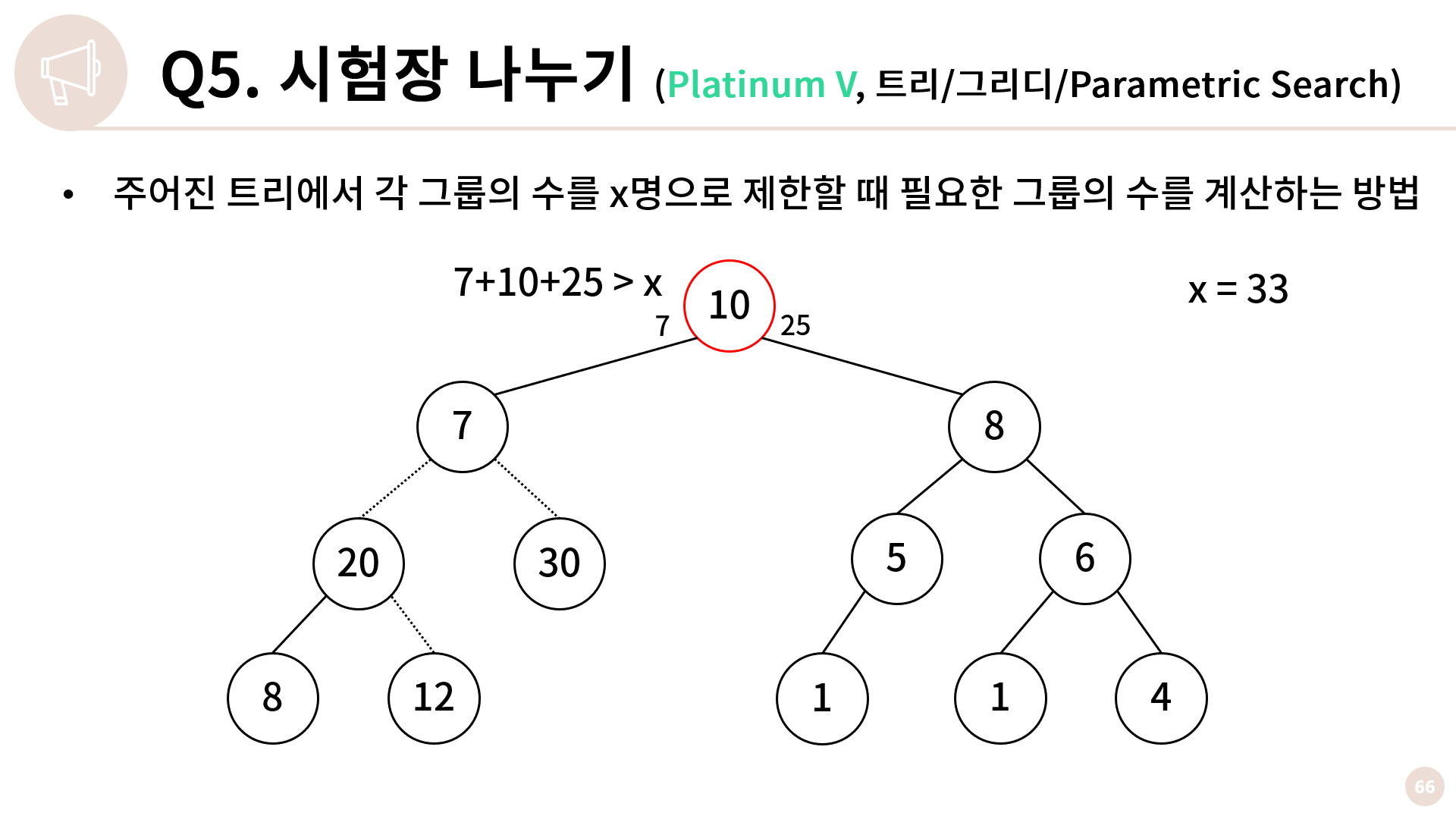
오른쪽에 있는 1, 1, 4, 5, 6, 8은 계속 위로 쭉쭉 올리게 되니 생략하고 루트를 봅시다. 루트에서는 왼쪽 자식에서 7이 넘어오고 오른쪽 자식에서 25가 넘어오고, 7+10+25가 33보다 크기 때문에 둘 다 챙겨갈수는 없습니다.
7을 가져가고 25를 끊어냅니다. 이렇게 총 4번 끊어냈고 5개의 그룹이 생겨난 것을 확인할 수 있습니다.

이렇게 리프에서부터 올라가면서 그룹의 정원이 차기 전까지 위로 값을 올려보내는 작업을 반복하면 되고, 왼쪽 자식과 오른쪽 자식으로부터 받은 값에 따라 위의 그림과 같은 처리를 해주면 됩니다. 이를 dfs로 구현하면 코드가 깔끔하게 구성됩니다.
트리가 일자인 경우 재귀 깊이가 최대 10000일 수 있기 때문에 sys.setrecursionlimit(10**6)를 통해 재귀 깊이를 늘려주어야 합니다.
관련 강의
0x11강 - 그리디
0x13강 - 이분탐색
0x19강 - 트리
'알고리즘 > Programmers' 카테고리의 다른 글
| [2022 KAKAO Blind Recruitment] Q3. 주차 요금 계산 (C++, Python, Java) (0) | 2022.01.17 |
|---|---|
| [2022 KAKAO Blind Recruitment] Q2. k진수에서 소수 개수 구하기 (C++, Python, Java) (0) | 2022.01.17 |
| [2022 KAKAO Blind Recruitment] Q1. 신고 결과 받기 (C++, Python, Java) (0) | 2022.01.17 |
| [2021 카카오 채용연계형 인턴십] Q4. 미로 탈출 (C++, Python, Java) (3) | 2021.08.16 |
| [2021 카카오 채용연계형 인턴십] Q3. 표 편집 (C++, Python, Java) (4) | 2021.08.16 |
| [2021 카카오 채용연계형 인턴십] Q2. 거리두기 확인하기 (C++, Python, Java) (2) | 2021.08.16 |