
안녕하세요, 드디어 무려 0x09강에서 BFS를 배울 때 처음 언급했던 그래프를 소개해드릴 수 있게 됐습니다. 그래프도 자료구조의 일종이지만 실제로도 다른 대학 교재나 뭐 기타 알고리즘 교재들을 보면 자료구조 중에서 보통 웬만하면 그래프를 거의 마지막에 배웁니다. 그래서 이 강의에서도 이렇게 후반부에 다룰 수 있게 됐습니다.

이렇게 일단 정의를 알아보고 과연 그래프에서 BFS, DFS를 어떻게 하는건지를 설명드릴 예정입니다.

그러면 일단 그래프가 뭐냐고 했을 때 비트코인 이더리움 가즈아할 때 그 그래프는 아닙니다. 어차피 초반부니까 딴소리를 좀 하고 가면 제가 올해 2월쯤에 컴퓨터를 샀습니다. 17년도부터 원래 쓰던건 글카 750ti가 달려있던 컴퓨터였고 그건 본가에 두고 왔어서 제가 한동안 컴퓨터가 없었습니다. 그러다가 마침 컴을 사려고 하던 그때 3000번대 글카가 나와서 보통 출시땐 비싸니까 좀 가격 추이를 보다가 사야겠다 하고 있었었습니다. 그런데 갑자기 코인이 난리가 나가지고 글카가 말 그대로 대란이 났습니다. 그래서 아 이걸 좀 기다려야 하나 아니면 그냥 빨리 사야하나 엄청 고민을 하다가 노트북만 하나 있으니까 조금 그래가지고 그냥 모르겠다 하고 샀습니다. 그리고 그 이후로 그래픽카드 값은 고공행진을 하더니 제가 거의 사실상 막차 탄 느낌이었습니다. 그리고 제 글카는 현재 광산에 끌려가서 열심히 이더리움을 캐고 있습니다. 아마 주인을 엄청 욕하고 있겠죠? 아무튼 한달에 한 12만원 정도 벌리고 있으니 은근 쏠쏠합니다. 강의를 만들고 있는 지금도 제 글카는 열일을 하고 있습니다.
아무튼 그래프가 뭐냐고 했을 때 자료구조에서 말하는 그래프는 정점과 간선으로 이루어진 자료구조를 말합니다. 이진 검색 트리 단원에서 정점과 간선은 얘기가 한 번 나왔었습니다. 그리고 이 때 차수(degree)라는 개념을 알면 좋은데, 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수가 바로 차수입니다. 그래프는 네비게이션에서 최단 경로 찾기, 혹은 구글 같은 검색엔진에서 랭킹 정하기와 같이 뭔가 원소 사이의 연결 관계를 설정해야 하는 상황에서 유용하게 활용될 수 있는 자료구조입니다.

그리고 그래프의 간선에는 방향성이 있을 수 있습니다. 왼쪽처럼 방향성이 없다면 무방향 그래프라고 하고 방향성이 있다면 방향 그래프라고 합니다. 간선에 방향성이 있다는건 마치 일방통행 도로를 생각하면 됩니다.
방향 그래프에서도 차수라는 개념이 있는데 자기에게서 나가는 간선의 개수는 outdegree이고 들어오는 간선의 개수는 indegree입니다. 찾아보니 outdegree는 진출 차수, indegree는 진입 차수라고 부르기도 하던데 저는 개인적으로 저 한글 용어가 입에 별로 익숙하지 않습니다.
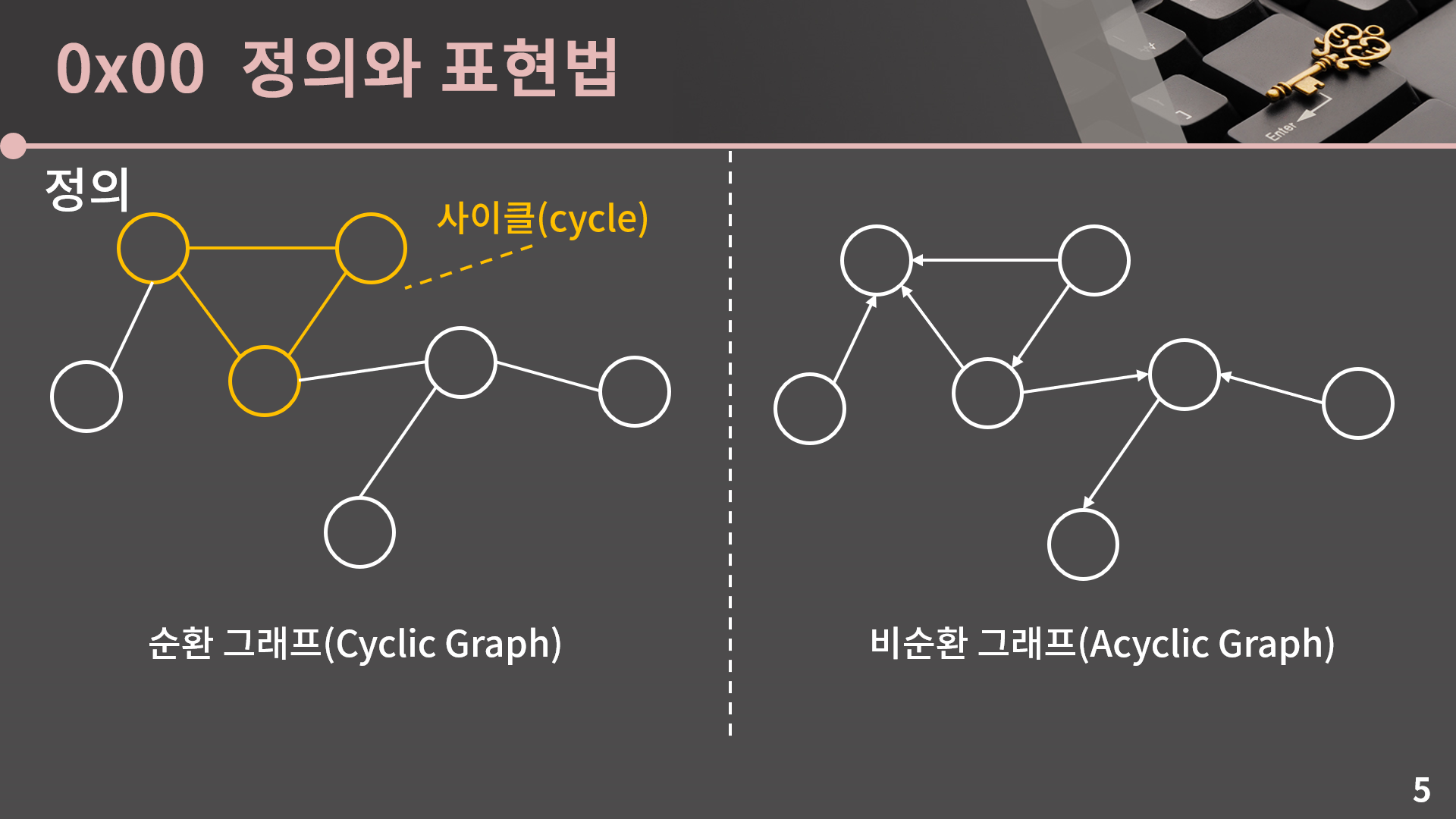
다음으로는 사이클인데, 임의의 한 점에서 출발해 자기 자신으로 돌아올 수 있는 경로를 사이클이라고 합니다. 그래프 안에 사이클이 하나라도 있으면 순환 그래프(Cyclic graph)라고 하고 사이클이 하나도 없으면 비순환 그래프(Acyclic graph)라고 합니다. 이 정의는 그래프가 방향 그래프인지 무방향 그래프인지 무관하게 동일하고 오른쪽의 경우에는 얼핏 보면 왼쪽처럼 사이클이 있는 것 처럼 보이지만 간선의 방향성으로 인해 사이클이 없다는거에 유의합시다.

또한 모든 서로 다른 두 정점 쌍이 간선으로 연결된 그래프를 완전 그래프(Complete Graph)라고 부릅니다. 그리고 임의의 두 정점 사이에 경로가 항상 존재하는 그래프는 연결 그래프(Connected Graph)라고 부릅니다.

그래프는 꼭 연결되어 있을 필요도 없고, 또 두 정점 사이의 간선이 반드시 1개 이하일 필요도, 또 간선이 반드시 서로 다른 두 정점을 연결해야 할 필요도 없습니다. 좀 이질적이긴 하지만 아무튼 한 정점에서 시작해 같은 정점으로 들어오는 간선이 있을 수도 있습니다. 이런 간선을 우리는 루프(loop)라고 부릅니다.
보통 문제에서는 필요에 따라 "그래프는 연결되어 있다/그래프는 연결그래프이다", "두 정점 사이의 간선은 최대 1개 존재한다/같은 간선은 한 번만 주어진다", "간선의 두 정점은 서로 다르다/간선은 서로 다른 두 정점을 연결한다"와 같이 조건을 엄밀하게 지정하는 경우가 많습니다. 그러나 이러 추가적인 조건이 주어지지 않았다면 그림에 있는 그래프처럼 그래프가 분리되어 있거나, 같은 간선이 여러 개 있거나, 혹은 루프가 있거나 하는 형태에 대해서도 올바른 답을 낼 수 있게 코드를 짜야한다는걸 기억해야 합니다. 참고로 두 정점 사이의 간선이 1개 이하이고 루프가 존재하지 않는 그래프를 우리는 단순 그래프(Simple Graph)라고 합니다.

그래프라는 개념 자체는 오며가며 한번씩 들어봤거나 배운 적이 있어서 알고는 있지만 이것을 어떻게 코드로 표현해야 할지 모르는 프로그래머가 되게 많습니다. 지금 강의를 듣고 있는 여러분들이야 배우는 과정이니까 당연히 모를 수 있습니다. 그런데 제가 오리엔테이션에서도 말을 했었지만 코로나로 이 난리가 나기 전에, 그러니까 2019년에 삼성전자 인재개발원에서 직원분들을 대상으로 역량강화교육 이러면서 B형 등급을 취득하실 수 있게 교육을 시켜드리는 연수 프로그램에 강사로 참여한 적이 있습니다. 제가 메인이 되어서 주도적으로 한건 아니고 미리 짜여있는 커리큘럼을 따라가면 되는거였는데 제가 갔던 날 주제가 그래프였습니다. 그런데 거기서 수강하시는 분들 중에서 애초에 입력을 보고 이걸 어떻게 코드로 옮겨야 하는지 자체를 모르는 분들이 꽤 있었습니다. 그러니까 제가 하고 싶은 말은, 심지어 삼성전자에 합격해서 회사 일을 잘 해내고 계신 직원들조차도 이걸 모르시는 분들이 꽤 있었습니다. 그래서 지금 배우시는 입장인 여러분이 설명 들어도 좀 어렵다, 잘 모르겠다 이거 맞나 하면서 남들은 다 잘 하는 것 같은데 나만 이렇게 힘든건가 하고 생각할 필요는 없습니다. 아마 뭐 맞왜틀하고 개념 이해 잘 안가서 며칠 고생하고 이런건 다 똑같습니다. 옛날에 좀 배웠던 사람이라고 하더라도 기억이 가물가물해서 결국 다시 풀고 뭐 그런 일의 반복입니다. 뭐 당장 저도 처음 공부할때는 그랬습니다. 또 취준이든 아니면 그냥 개인적인 공부 목적이든 이렇게 한 번 제대로 해두면 앞으로 개발자로 일할 때 정말 도움이 될거니 스스로의 발전에 만족하면서 남은 강의들을 잘 헤쳐나가봅시다.

첫 번째 방법은 인접 행렬을 이용하는 방식입니다. 편의상 단순 그래프, 즉 두 정점 사이의 간선이 1개 이하인 그래프라고 할 때 연결된 두 정점에는 1을, 연결되지 않은 두 정점에는 0을 주면 그래프를 표현할 수 있습니다. 지금은 무방향 그래프여서 자연스럽게 왼쪽 위와 오른쪽 아래를 연결하는 대각선에 대해 대칭인 형태가 나옵니다.

만약 방향 그래프였다면 이런 식으로 표현이 가능합니다. (2, 3)이 1이라는 의미는 2에서 3으로 가는 간선이 있다는 의미입니다. 엄밀히 말해서 1 혹은 0으로만 나타내는 이 표현법은 두 점을 잇는 간선이 여러 개일 경우 문제가 생길 수 있지만 일반적으로는 대부분의 문제에서 주어지는 그래프는 단순 그래프이긴 합니다. 만약 단순 그래프가 아니라고 한다면 1 혹은 0으로만 나타내지 말고 간선이 3개면 3을 쓰고, 4개면 4를 쓰고 이런 식으로 변형을 시키면 쉽게 해결이 됩니다.
인접 행렬로 그래프를 나타내면 정점이 V개이고 간선이 E개일 때 어떤 두 점이 연결되어 있는지를 O(1)에 알 수 있다는 장점이 있습니다. 그리고 가로와 세로가 각각 V인 2차원 배열이 필요하니 O(V2)의 공간을 필요로 합니다. 또 어떤 점에 연결되어 있는 모든 정점의 목록을 알아내고 싶을 때에도 개수와 무관하게 시간복잡도가 O(V)입니다.

나중에 문제를 보시면 알겠지만 보통 그래프 관련 문제에서 입력이 지금 적혀있는 것 처럼 주어집니다. 처음에 정점 개수를 주고, 그 다음에 간선 개수를 주고, 7개의 간선을 쓰는 방식입니다. 예를 들어 3에서 1로 가는 간선이 있으니까 3 1이고 그 다음에 2 3이고 이런식으로 간선이 주어집니다. 그리고 관례적으로 보통 웬만하면 정점은 1-indexed로 번호를 붙입니다. 그러니까 1번부터 V번까지의 정점이 있습니다. 이 입력을 인접 행렬로 나타내고자 하면 구현은 되게 간단합니다.

먼저 방향 그래프의 예시를 보면 adj_matrix 배열을 선언한 후에 간선을 입력 받으면서 adj_matrix[u][v] = 1로 만들면 끝입니다. 만약 이게 무방향 그래프였다고 하면 adj_matrix[u][v]와 adj_matrix[v][u]를 모두 1로 만들면 됩니다. 지금까지 소개한 방법이 바로 인접 행렬을 이용하는 방법입니다.

그리고 그래프를 나타내는 두 번째 방법은 인접 리스트를 이용하는 방법입니다. 이 방식은 인접 행렬과 비교했을 때 정점이 많고 간선은 상대적으로 작은 상황에서 공간을 절약할 수 있는 방식이고, 경우에 따라 인접 행렬로는 절대 저장이 불가능해 인접 리스트를 써야만 하는 상황이 종종 있어서 반드시 익숙하게 사용할 수 있어야 합니다.
인접 리스트의 개념 자체는 크게 어렵지는 않습니다. V개의 리스트를 만들어 각 리스트에 자신과 연결된 정점을 넣으면 끝입니다. 지금 이 인접 리스트는 무방향 그래프인 상황에서의 인접 리스트입니다.
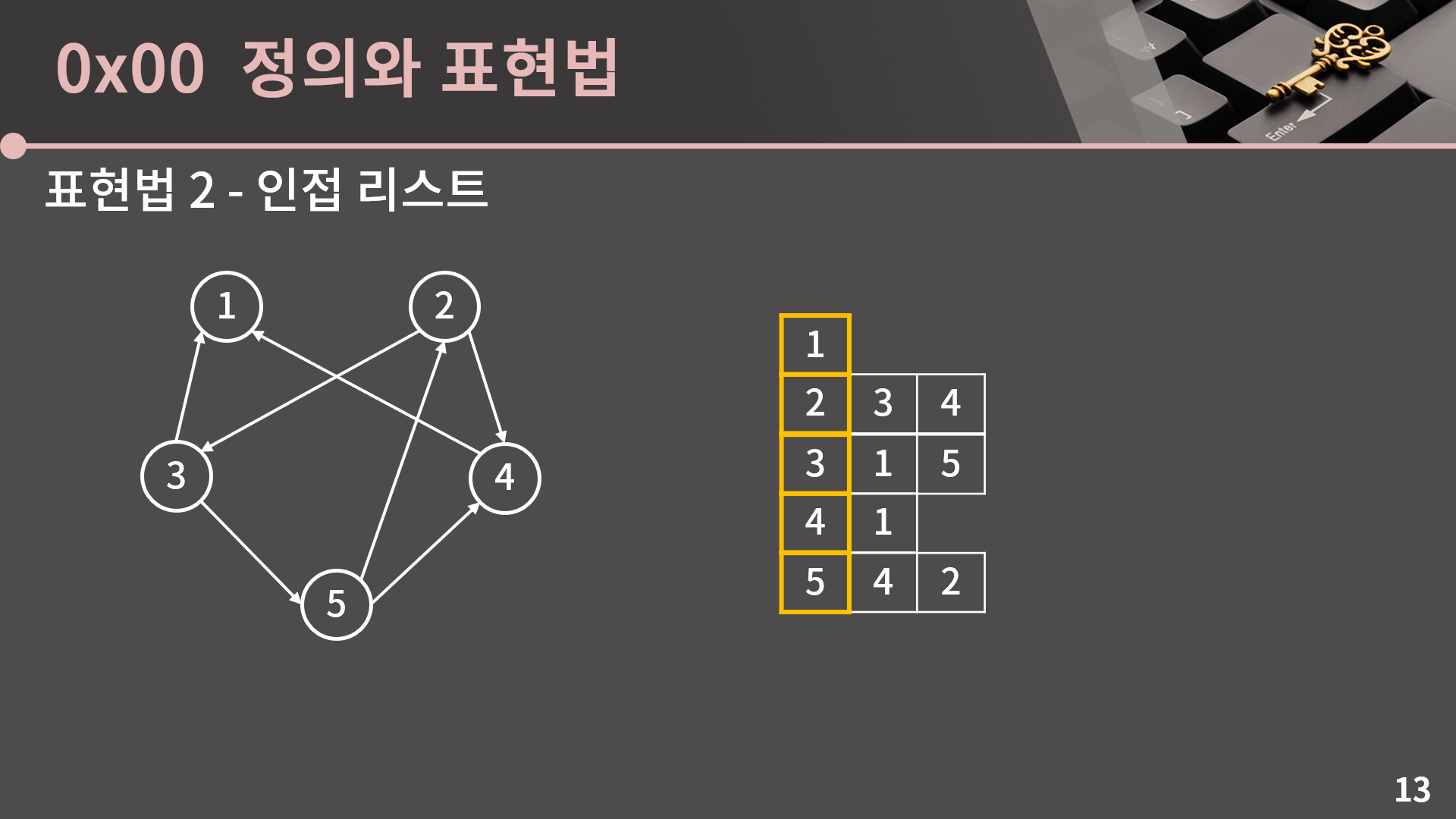
만약 방향 그래프라고 하더라도 크게 달라지는건 없습니다. 방향 그래프라면 양쪽에 다 넣는게 아니라 한 쪽에만 넣으면 됩니다. 인접 행렬에서는 V by V 크기의 배열을 선언했어야 하니 O(V2)의 공간이 필요했는데 인접 리스트에서는 O(V+E)의 공간이 필요합니다. 일단 리스트가 V개 필요하고, 간선이 1개 있을 때 마다 방향 그래프에서는 특정 리스트 1개에 원소가 1개 추가되고 무방향 그래프에서는 특정 리스트 2개에 원소가 1개씩 추가됩니다. 그렇기 때문에 모든 리스트에서 원소의 개수의 총합은 방향 그래프일 때 E개, 무방향 그래프일 때 2E개이기 때문에 최종적으로 O(V+E)라는걸 알 수 있습니다.

문제는 이걸 어떻게 구현하는가인데, 리스트라고 해서 진짜 연결 리스트인 STL list를 쓸 필요는 없고 그냥 vector를 가지고 구현하는게 편합니다. adj[i]는 정점 i와 연결된 정점들의 목록을 가지고 있는 vector이고 또 여기서도 방향 그래프인지 무방향 그래프인지에 따라서 adj[u]에만 값을 넣을지 adj[u]와 adj[v]에 모두 값을 넣을지 결정해주면 됩니다.

자 그런데 STL을 못쓰면 어떻게 해야할까요? 이게 조금 문제입니다. 요새는 사실 트렌드가 STL이나 뭐 기타 언어에서 제공하는 라이브러리를 굳이 못쓰게 하는 일이 잘 없는데 제가 아는 범위에서 유일하게 삼성이 B형에서 그런 제한을 걸다보니 이걸 소개를 살짝 드리겠습니다.
STL을 쓸 수 없는 환경일 때는 조금 까다로운게, 예를 들어 정점이 100,000개이고 간선은 최대 500,000개인 그래프가 주어진다고 해보겠습니다. 이 때 그래프가 단순그래프라면 각 정점의 차수는 최대 99,999일 수 있습니다. 즉 한 리스트에 최대 99,999개의 정점이 들어갈 수 있습니다. 그러면 만약 그냥 리스트를 정적 배열로 선언을 하겠다 해버리면 100,000개의 리스트를 전부 크기 99,999개의 배열로 잡아야 한다는 의미인데 이렇게 되면 공간복잡도가 O(V2)가 되니 공간 복잡도가 인접 행렬과 다를 것이 없어지고 결정적으로 V가 100,000인 이상 이렇게 선언을 하면 그냥 메모리 초과입니다. 조금 앞에서 삼전 인재개발원에서 역량강화교육 얘기한 것도 사실 그 직원분들이 인접 리스트를 모르는건 아닌데 이걸 STL 없이 짜야 하니 좀 당황을 하셨던 상황이었습니다. 가장 직관적이고 어떻게 보면 가장 정석적인 방법은 그냥 직접 vector같은 동적 배열이나 list 같은 연결 리스트 기능을 하는 클래스를 만들어서 쓰는 방법입니다. 이게 가장 정석적인 방법인데 짐작하다시피 아무래도 실수할 여지가 많습니다. 그리고 배보다 배꼽이 큰 느낌인게, 나는 진짜 그냥 그래프만 저장하면 되는데 vector나 list같은거 매번 새로 짜야 한다면 한숨밖에 안나옵니다. 그러면 대신에 어떻게 좀 영리하게 할 수 있냐면 이 코드를 한 번 확인해봅시다.

먼저 방향 그래프의 예시인데, 일단 간선의 목록을 입력받습니다. 그리고 이 때 outdegree를 셉니다. outdegree를 세고 나면 각 리스트의 크기가 정해집니다. 그러면 이후 차수에 맞게 동적 배열을 잡는 식으로 구현을 하면 STL이 없어도 굉장히 간단하게, 또 추가적인 복잡한 구현을 필요로 하지 않게 인접 리스트 방식을 구현할 수 있습니다. 다시 한 번 말하지만 STL을 쓸 수 있으면 그냥 vector를 쓰면 됩니다. 이건 STL을 못쓸 때 이렇게 하면 된다 하고 알려드린겁니다.

그리고 무방향 그래프라고 하면 양쪽으로 넣어줘야 한다는 것만 신경을 잘 쓰면 됩니다. 구조는 그냥 똑같습니다. 한 번 코드를 살펴봅시다.

마지막으로 두 표현법을 비교해보면 우선 공간 복잡도는 인접 행렬의 경우 O(V2)이고 인접 리스트의 경우 O(V+E)입니다. 다음으로 임의의 두 정점이 연결되어 있는지 확인하는 시간 복잡도의 경우, 인접 행렬은 그냥 adj_matrix[u][v]를 확인하면 되니 O(1)입니다. 반면 인접 리스트에서는 한 정점에 대해 자신과 연결된 모든 정점을 확인해야 하는데, 둘 중에서 차수가 작은 것을 택해서 확인하는게 이득이니까 O(min(deg(u), deg(v))입니다. deg(u)는 정점 u의 차수를 의미합니다. 한 정점이 연결된 모든 정점을 확인하는 시간 복잡도의 경우에는 인접 행렬은 1번부터 V번까지에 대해 연결관계를 전부 확인해야 하므로 O(V)이지만 인접 리스트에서는 O(deg(v))입니다.
정리하면 인접 행렬은 두 점의 연결여부를 많이 확인할 때, 혹은 간선의 개수가 V2에 가까울 때 효율적입니다. 반대로 인접 리스트는 특정 정점에 연결된 모든 정점들을 자주 확인할 때, 혹은 간선의 개수가 V2보다 훨씬 적을 때 효율적입니다. 예를 들어 V가 100,000이고 E가 200,000일 경우에는 간선의 개수 E가 V2보다 훨씬 작기 때문에 인접 리스트를 사용하는 것이 효율적입니다. 사실 애초에 256MB나 512MB 같은 일반적인 메모리 제한이 있는 상황에서는 V가 100,000이면 인접 행렬로 나타낼 수가 없습니다. 반대로 V가 100이고 E가 7,000일 경우에는 인접 행렬을 사용하는 것이 효율적이입니다.
그런데 일반적인 그래프 문제에서 정점 u, v가 연결되어있는지를 반복적으로 확인해야 하는 경우는 잘 없습니다. 그리고 다음 챕터에서 배우게 될 BFS, DFS나 앞으로 배울 여러 경로 알고리즘들에서는 전부 특정 정점에 연결된 모든 정점을 확인하는 작업이 반복적으로 등장합니다. 그렇기 때문에 앞으로 인접 행렬 보다는 인접 리스트로 그래프를 나타낼 상황이 훨씬 많습니다. 다만 입력 자체가 인접 행렬 느낌으로 주어지거나 V가 많이 작아 구현의 편의를 챙기고자 하거나, 아니면 최단경로 알고리즘 중 하나인 플로이드 알고리즘을 쓸 때에는 인접 행렬로 그래프를 나타내는 경우가 있을 수 있긴 합니다. 그래서 두 방법 모두 지금 이해한 정도로 알고 계시면 됩니다.

이제 BFS를 다룰 시간입니다. 아마 여기까지 오신 분들이라면 0x09강 - BFS 단원에 있던 수많은 BFS 문제들을 풀면서 BFS에 좀 익숙하실 것 같습니다. 그리고 BFS 단원에서 BFS를 어떻게 설명했는지 그대로 가져와보겠습니다. "BFS는 다차원 배열에서 각 칸을 방문할 때 너비를 우선으로 방문하는 알고리즘입니다. 원래 BFS는 그래프라는 자료구조에서 모든 노드를 방문하기 위한 알고리즘이고, BFS를 정확하게 이해하려면 그래프 자료구조에 대한 이해가 선행되어야 하는데 아직은 그래프를 안배워서 더 설명은 힘들고 실제 동작을 보면서 이해해봅시다" 이렇게 설명을 했습니다. 그리고 지금은 그래프를 배웠으니 제대로 설명을 할 수가 있습니다. 사실 순서로 보면 그래프를 배운 후에 BFS를 배우는게 맞긴 한데 다차원 배열에서 BFS를 하는 문제가 워낙 잘 나와서 어쩔수없이 그래프 개념을 배제한 상태로 BFS를 앞에서 다룬 후에 지금에야 제대로 소개를 드릴 수 있게 됐습니다.
BFS는 그래프에서 너비를 우선으로 방문하는 알고리즘입니다. 그 전에 다차원 배열에서 BFS가 잘 정의됐던 이유는 여기 그림처럼 다차원 배열을 그래프로 나타낼 수 있기 때문입니다. 다차원 배열에서의 BFS에 충분히 익숙하다면 그래프에서 BFS를 하는 것도 큰 어려움 없이 이해할 수 있습니다.

일단 방법을 글로 나타내봤습니다. 보면 좀 익숙합니다. 다차원 배열에서는 2번 과정에서 상하좌우로 인접한 칸을 확인했던 반면에 이번에는 간선으로 연결된 정점을 본다는 차이만 있습니다. 그리고 시간복잡도에 대해서 얘기를 해보면 일단 인접 행렬에서는 특정 정점과 연결된 모든 정점을 확인하는 2번 과정이 O(V)를 필요로 하고 또 2번 과정 자체가 V개의 모든 정점에 대해 실행될 수 있으니 O(V2)인게 쉽게 이해가 됩니다. 그런데 인접 리스트에서 왜 O(V+E)인지 조금 헷갈릴 수 있는데, 2번 과정에서 모든 정점들에 대해 그 정점과 연결된 모든 정점을 살펴보는 과정의 총 합이 방향 그래프에서 E, 무방향 그래프에서 2E여서 그렇습니다. 조금 헷갈리면 다음 슬라이드를 같이 보겠습니다.
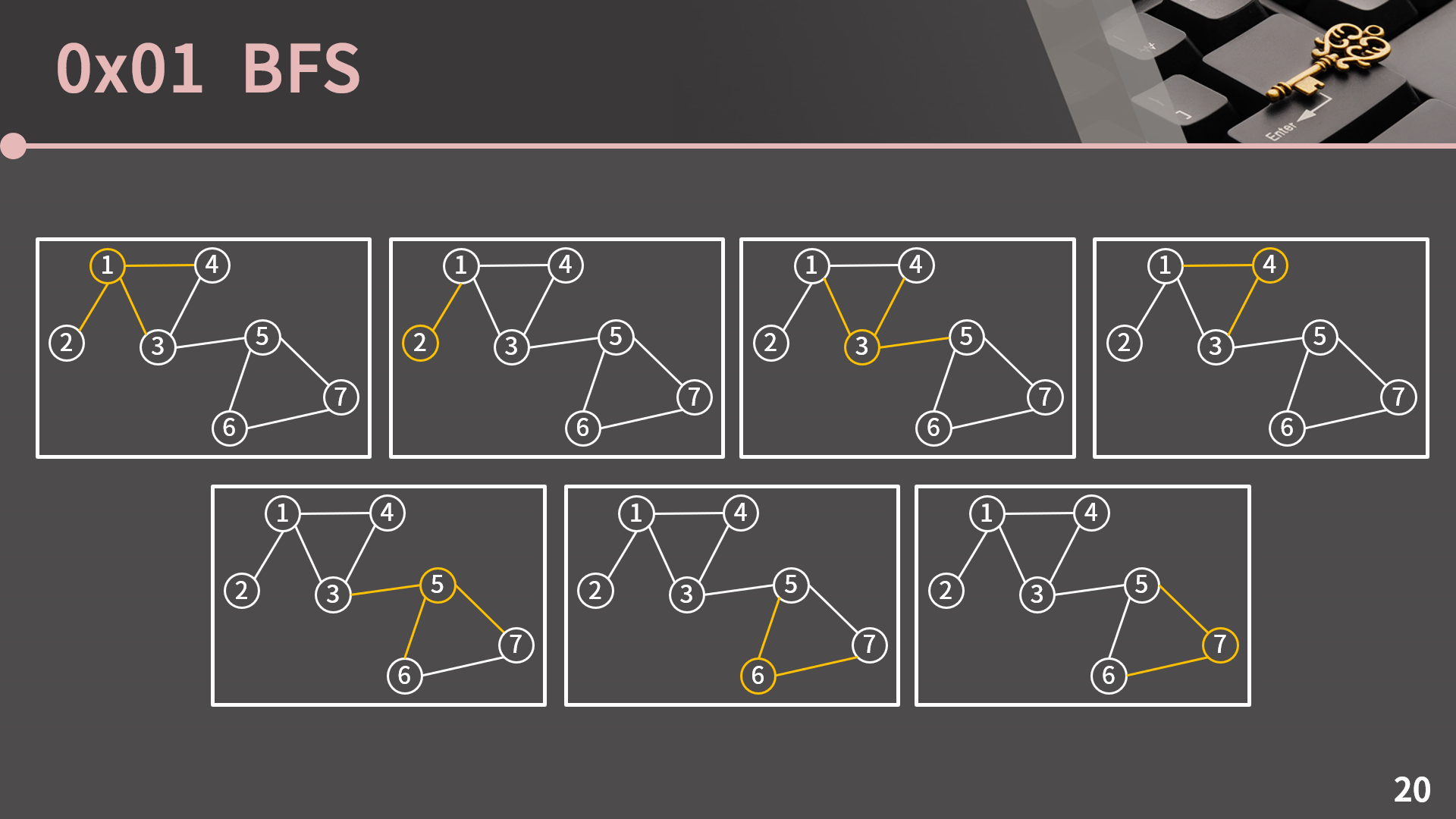
모든 정점들에 대해 그 정점과 연결된 모든 정점을 살펴보는 과정의 총 합이 무방향 그래프에서 2E이다 라는 말을 그림으로 이해시켜 드리겠습니다. 현재 그래프에 간선은 8개입니다. 7개의 각 그래프는 1번부터 7번까지의 정점이 자신과 연결된 정점을 탐색하는 상황을 나타낸 그림입니다. 그림을 살펴보면 각 간선은 2번씩 등장합니다. 이는 논리적으로 생각해도 당연한게 u와 v를 연결하는 간선은 u와 연결된 모든 정점을 살펴볼 때, 그리고 v와 연결된 간선을 살펴볼 때 한 번씩 등장하기 때문입니다. 그리고 만약 방향 그래프였다면 u에서 v로 가는 간선은 u와 연결된 모든 정점을 살펴볼 때에만 등장합니다. 그렇기 때문에 앞에서 설명한, 모든 정점들에 대해 그 정점과 연결된 모든 정점을 살펴보는 과정은 2E번 혹은 E번의 탐색을 필요로 하고 이로 인해 시간복잡도가 O(V+E)가 됩니다.
다차원 배열에서의 BFS는 그냥 간선이 각 칸마다 최대 4개만 있는 상황이었다 보니 그냥 시간복잡도가 칸 수에 비례한다고 쉽게 생각을 할 수 있었습니다. 그런데 그래프에서는 시간복잡도에 E가 포함된다는 것을 유념하셔야 합니다. 예를 들어 V가 2,000인 완전 그래프를 생각해보겠습니다. 완전 그래프는 모든 서로 다른 두 정점 쌍이 간선으로 연결된 그래프를 말합니다. 그러면 간선은 대략 2,000,000개인데 여기서 BFS를 1000번 돌리는 풀이를 생각한 경우 이것의 시간복잡도는 O(1000V)가 아니라 O(1000(V+E))여서 시간초과가 발생합니다. BFS 과정은 안보여드려도 알아서 잘 이해하실 것 같긴 한데 어차피 예전에 만들어 놓은게 있으니까 복습 차원에서 같이 한번 확인해보겠습니다.
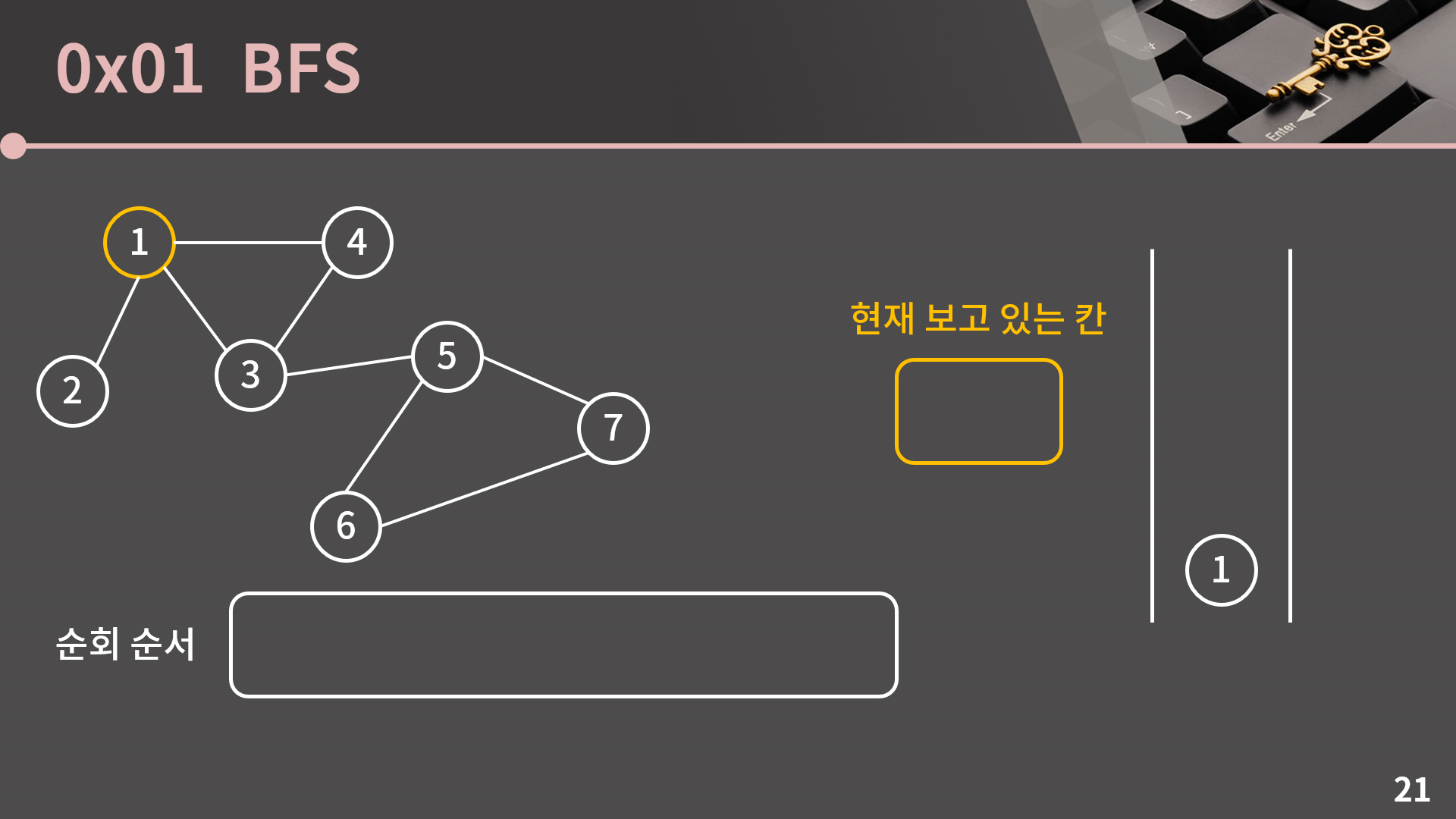
시작 정점은 어느 것이어도 상관이 없지만 임의로 1번부터 시작해보겠습니다. 일단 1번 정점을 큐에 넣고 방문했다는 표시를 남깁니다.

큐가 비어있지 않으니까 큐의 front인 1번 정점을 꺼냅니다.

1번 정점과 이웃한 2, 3, 4번 정점은 모두 아직 방문하지 않은 정점이니까 방문했다는 표시를 남기고 큐에 넣습니다.

큐가 비어있지 않으니까 큐의 front인 2번 정점을 꺼냅니다. 2번 정점과 이웃한 1번 정점은 이미 방문한 정점이기 때문에 넘어갑니다.

큐가 비어있지 않으니까 큐의 front인 3번 정점을 꺼냅니다.

3번 정점과 이웃한 정점은 1, 4, 5번 정점입니다. 이 중에서 5번 정점만 유일하게 방문하지 않은 정점이기 때문에 방문했다는 표시를 남기고 큐에 넣습니다.

큐가 비어있지 않으니까 큐의 front인 4번 정점을 꺼냅니다. 4번 정점과 이웃한 1, 3번 정점은 이미 방문한 정점이므로 넘어갑니다.
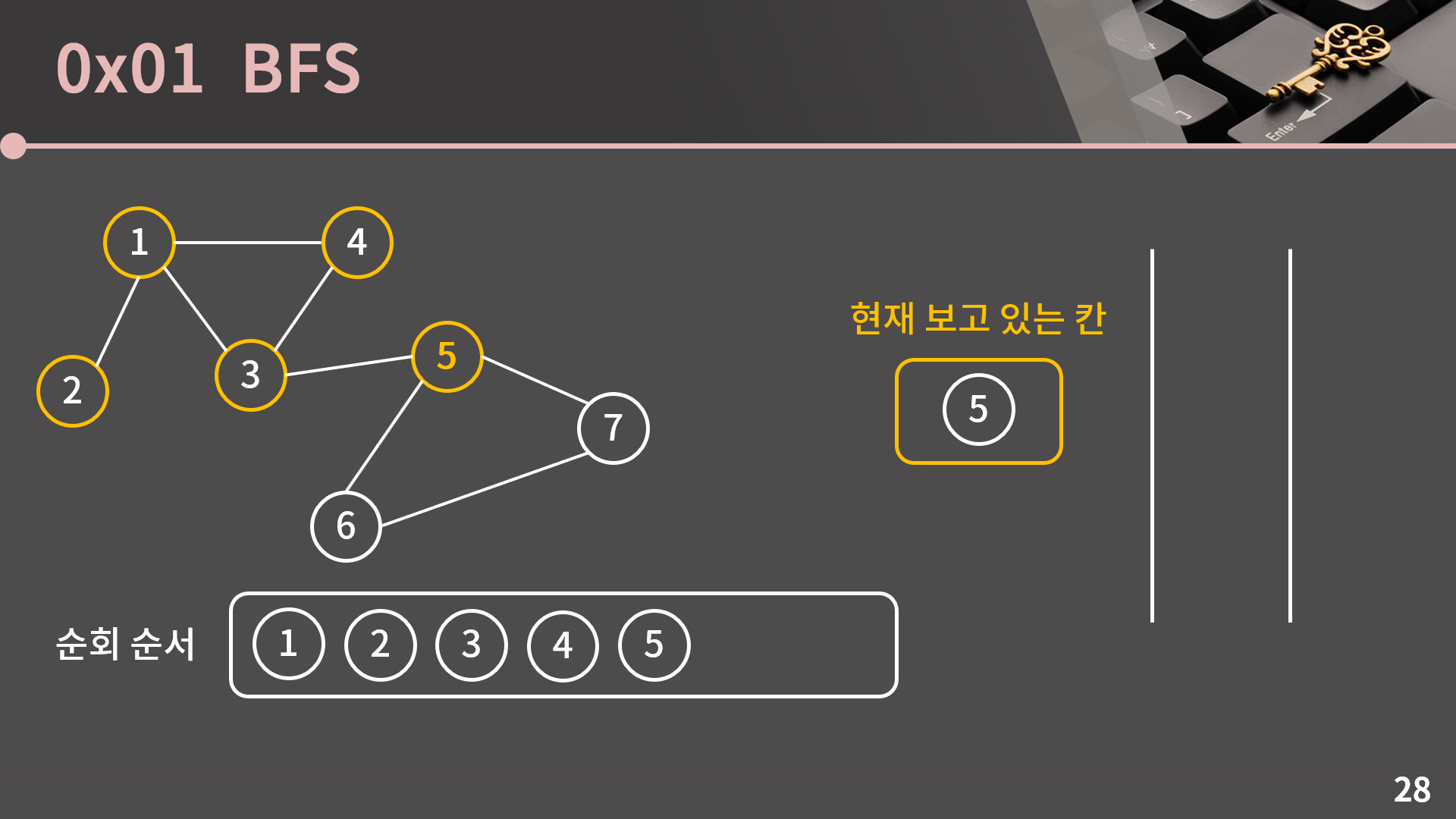
큐가 비어있지 않으니까 큐의 front인 5번 정점을 꺼냅니다.
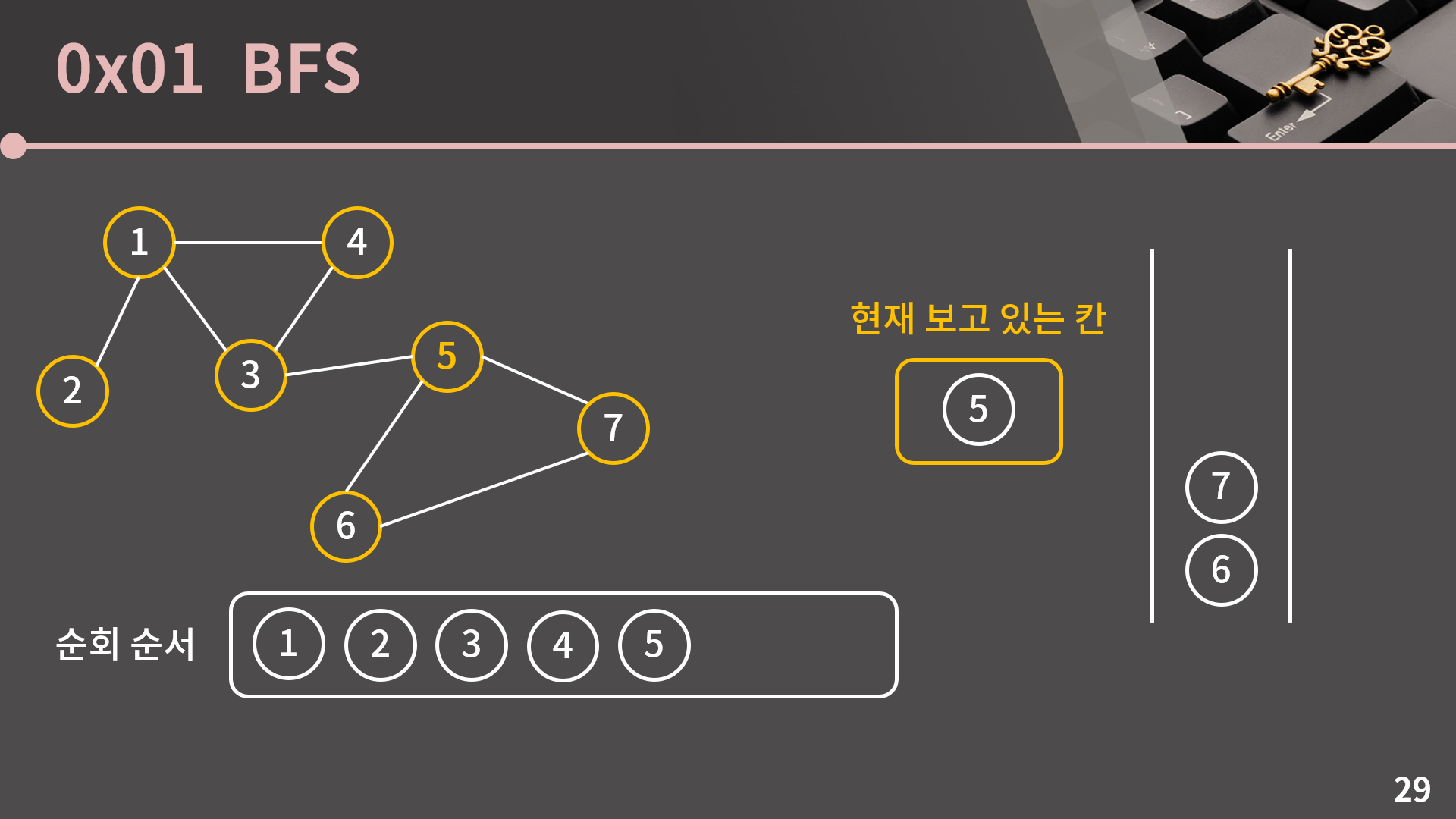
5번 정점과 이웃한 3, 6, 7번 정점 중에서 3번 정점은 이미 방문한 정점입니다. 6, 7번 정점은 아직 방문하지 않은 정점이기 때문에 방문했다는 표시를 남기고 큐에 넣습니다.

큐가 비어있지 않으니까 큐의 front인 6번 정점을 꺼냅니다. 6번 정점과 이웃한 5, 7번 정점은 이미 방문한 정점이므로 넘어갑니다.

큐가 비어있지 않으니까 큐의 front인 7번 정점을 꺼냅니다. 7번 정점과 이웃한 5, 6번 정점은 이미 방문한 정점이므로 넘어갑니다.

이제는 큐가 비었으니 과정이 끝납니다. BFS에 익숙하다면 크게 어려울 건 없을 것 같습니다.

BFS 단원에서 응용을 소개할 때 다룬 내용이지만 그래프에서도 시작점에서 다른 모든 점으로의 최단 경로를 찾을 때 BFS를 이용할 수 있습니다. BFS의 과정 중에서 현재 보는 정점으로부터 추가되는 인접한 정점은 시작점으로부터 1만큼 더 떨어져 있습니다. 즉 모든 간선의 길이가 동일한 상황에서 두 지점 사이의 거리를 찾는 문제는 BFS로 해결이 가능합니다. 하지만 만약 모든 간선의 길이가 다르다면 이 문제는 플로이드나 다익스트라와 같은 다른 알고리즘을 사용해야되고 이러한 알고리즘은 나중에 다룰 예정입니다.

실제로 인접 리스트 방식으로 저장된 그래프에서 BFS를 진행하는 코드를 같이 보겠습니다. 정점은 1번부터 V번까지 순차적으로 매겨져있다고 가정하겠습니다. 이미 2차원 배열에서 BFS를 많이 해보았기 때문에 코드의 흐름이 크게 낯설지 않을 것 같습니다. 큐에 넣은 직후에 vis의 값을 true로 갱신해줘야 함에 유의해야 하고, 인접 행렬로 BFS를 구현하면 시간복잡도가 O(V2)으로 더 비효율적이라 비추천하지만 굳이 필요하다면 for문 부분을 for(int nxt = 1; nxt <= V; nxt++)으로 변경하고 adj_matrix[cur][nxt]가 1일 때만 아래의 과정을 진행하도록 코드를 수정하면 됩니다.

만약 1번 정점과의 거리가 필요하다면 dist 배열을 선언해서 잘 채우면 됩니다. 먼저 dist를 -1로 초기화한 후에 dist 배열이 -1인지 아닌지를 가지고 방문 여부를 판단하면 vis 배열을 별도로 둘 필요가 없습니다.

만약 연결 그래프가 아닌 그래프에서 순회를 하고싶다고 하면, 예시 코드 1 처럼 코드를 짰을 때 1, 2, 3, 4번 정점만 방문을 하게 됩니다. 이를 해결하기 위해서는 BFS 단원에서 BOJ 1926번: 그림 문제를 해결할 때 사용한 방법을 그대로 가져오면 되는데, for문을 돌면서 아직 방문하지 않은 정점을 찾아 그 정점을 시작 정점으로 잡게끔 코드를 변형하면 됩니다. 다음 슬라이드의 코드를 확인해보세요.

이미 BFS에서 신나게 구른 뒤에 지금 다시 BFS를 배우는거라 코드를 보면 아마 좀 익숙할 것 같습니다. 설명은 생략하겠습니다.

다음은 DFS인데 앞에서 DFS를 배울 때에는 그냥 BFS랑 같은데 큐를 스택으로 대체하기만 하면 된다, 다차원 배열을 순회하는 문제에서는 DFS가 필요하지 않으니 당장은 중요하게 생각을 하지 않아도 된다고 설명을 했습니다. 정말 말 그대로 BFS 과정에서 큐만 스택으로 바꾸면 DFS 과정이 됩니다.

코드도 한 번 보고 가겠습니다. 특이한게 없어서 설명은 패스하고 바로 넘어가겠습니다.

그런데 사실 DFS를 다룰 때 재귀를 빼놓을 수가 없습니다. DFS 단원에서는 당시 아직 재귀를 배우기 전이기도 했고, 또 당시 언급한 것 처럼 다차원 배열에서는 DFS가 필요한 상황이 없어서 설명을 안드렸었지만 DFS는 재귀를 이용해서 구현을 할 수 있습니다. 재귀적으로 함수를 호출하는 상황 자체가 가장 늦게 호출된 함수를 먼저 처리하는 LIFO, 즉 자연스럽게 스택을 이용하는 모양새가 되어서 그렇다고 생각할 수 있습니다.
일단 재귀로 DFS를 도는 코드를 확인해보면 다른 무엇보다 일단 코드가 짧습니다. 재귀에 충분히 익숙하다는 가정 하에, 재귀적으로 구현을 하게 되면 코드가 알아보기 쉽고 코드 길이도 짧아집니다. 그래서 당장 저도 DFS가 필요하면 재귀적으로 짜는걸 선호합니다. 그런데 재귀 단원에서 언급한 얘기지만 스택 메모리의 제한이 작은 경우에는 재귀 구현에는 아주 큰 문제가 있는데, 재귀적으로 들어갈 때 마다 메모리 중 스택 영역에 계속 데이터가 쌓입니다.

재귀 단원에서 가져온 그림인데 이게 메모리의 구조이고 여기서 스택 영역에 값이 쌓인다는 의미입니다. 그리고 예를 들어 그래프가 1 -> 2 -> 3 -> ... -> 100,000 와 같이 일자로 생겼으면 dfs 재귀 구현에서는 dfs(1) -> dfs(2) -> dfs(3) -> ... -> dfs(100,000)으로 호출이 진행됩니다. 이렇게 되면 스택 영역에 최대 함수 100,000개의 데이터가 쌓입니다. 보통 메모리 제한이 256, 512MB 이렇다고 할 때 원래라면 이 256MB나 512MB 제한에 절대 걸리지 않습니다. 그런데 온라인 저지중에 저 스택 영역의 메모리를 1MB나 10MB 처럼 작게 제한을 걸어두는 경우가 있습니다. 원래 기본적으로 스택 메모리의 제한이 작게 걸리게 되는데 거기서 설정을 따로 바꾸지 않아 이런 일이 생기게 됩니다. 이렇게 스택 메모리의 제한이 별도로 작게 설정된 곳에서는 재귀 대신 그냥 스택을 써서 DFS를 돌 수 밖에 없습니다. 다만 백준 온라인 저지에서는 별도의 스택 메모리 제한은 존재하지 않아 마음 편하게 구현을 하면 됩니다.
참고로 옛날에 되게 홍보를 떠들썩하게 하고 나름 큰 규모로 진행된 어떤 대회가 있었는데 그 대회의 본선 문제에서 LCA라는 알고리즘이 쓰이는 그래프 관련 문제가 나왔고 스택 메모리 문제로 인해서 DFS로 구현한 사람들이 죄다 런타임 에러를 받은 대참사가 난 적이 있었습니다. 저도 피해자 중 한 명이었는데, 심지어 마지막 문제는 정해에 오류가 있어서 맞왜틀을 외치다가 빡종을 했었습니다. 그래서 사실 스택 메모리는 당연히 주최측이 신경을 써줘야 하는 거지만 특히 코딩테스트라고 하면 설령 주최측이 스택 메모리 제한을 적게 둬서 내 재귀 DFS 코드가 틀렸다고 해도 그 결과를 되돌릴수는 없습니다. 그러니까 이 스택 메모리로 인해 재귀를 구현할 때 깊이가 깊어지면 문제가 있을 수 있다는걸 꼭 인지하시고, 처음 써보는 플랫폼에서 코딩테스트를 진행한다면 이 부분을 코딩테스트 전에 확인해두시는걸 추천드립니다. 지금 강의를 작성하고 있는 2021년 11월 기준 백준, 프로그래머스, 구름에서는 스택 메모리와 관련한 문제가 없었고 SW Expert Academy에서는 스택 메모리가 1MB로 제한이 되어 있었습니다.

이처럼 DFS를 구현하는 방식을 크게 재귀를 사용하는 방식과 재귀를 사용하지 않는 방식으로 나눌 수 있습니다. 두 방식 모두 특정 정점으로 시작해 도달할 수 있는 모든 정점을 순회하는 역할을 잘 수행합니다. 그런데 둘은 실제 동작에서 약간의 차이가 있는데, 이 예시를 한 번 보겠습니다. 주어진 그래프에서 재귀적인 방식으로 DFS를 돌면 1 2 4 3 순으로 방문을 합니다. 갈 수 있는 곳이 여러 개라면 번호가 작은 것 부터 방문한다고 할 때 dfs(1)은 dfs(2)를 부르고, dfs(2)는 dfs(4)를 부르고, dfs(4)는 dfs(3)을 부릅니다. 그런데 비재귀적인 방식으로 DFS를 돌면 맨 처음 1번 정점을 스택에서 뽑았을 때 이웃한 2, 3, 4번 정점에 모두 방문했다는 기록을 남겨놓고 다음 정점으로 넘어가기 때문에 1 2 3 4 순으로 방문을 합니다. 즉 재귀적인 방식은 실제 방문을 할 때 방문 표시를 남기는 반면에 비재귀적인 방식은 방문하기 전에 아직 방문하지 않은 곳을 발견하면 그 때 방문 표시를 남겨버리기 때문에 이러한 차이가 발생합니다.
엄밀히 말해 우리가 관념적으로 생각하는 DFS는 비재귀 DFS가 동작하는 방식과는 차이가 있고 재귀 DFS가 동작하는 방식과 일치합니다. 예전에 BFS와 DFS의 차이를 다룰 때 방문 순서를 확인해보면 BFS는 시작점에서 동심원이 생기는 것 처럼 상하좌우로 퍼져나가고, DFS는 뭔가 한 방향으로 막힐 때 까지 쭉 직진을 한다고 소개를 했었습니다. DFS를 미로를 가지고 비유하면 미로를 탈출하기 위해 갈림길에서 갈 수 있는 아무 방이나 찍어서 쭉 들어가다가 더 이상 갈 수 없으면 되돌아오는게 관념적으로 생각하는 DFS이고 갈림길에서 다른 방들에는 마크를 두고 한 방만 정해서 들어가는 방식은 아니기 때문입니다.
다시 한 번 강조하면 비재귀 DFS는 순회를 잘 수행하지만 엄밀히 말해 우리가 관념적으로 생각하는 DFS와 방문 순서가 다릅니다. 그래서 단순히 Flood Fill 내지는 순회를 하는 것이 아니라 DFS의 고유한 성질을 사용해 문제를 해결해야 하는 상황일 경우에는 앞에서 소개한 비재귀 코드를 이용하면 안됩니다.

그런데 앞에서 언급한 것 처럼 스택 메모리 문제로 인해 재귀를 사용할 수가 없는 상황이 있을 수 있습니다. 이럴 상황에서는 DFS가 필요할 때 재귀 없이 구현을 해야 하는데, 비재귀 또한 우리가 관념적으로 생각하는 DFS와 동일하게 동작하도록 바꿀 수 있습니다. 지금 이 코드와 이전에 저희가 맨날 쓰던 DFS 코드의 차이를 살펴보도록 합시다.
차이를 보면, 이전의 코드에서는 nxt를 스택에 넣은 직후에 바로 방문 여부, 즉 vis[nxt]를 true로 만들어 스택에 각 정점이 무조건 1번씩만 들어가도록 만들었습니다. 반면 지금의 코드는 스택에 넣을 때 방문 표시를 남기는게 아니라 스택에서 값을 뽑은 후에 방문 여부를 true로 만들도록 했습니다. 이렇게 수정하면 우리가 관념적으로 생각하는 DFS와 동작이 일치합니다. 이렇게 구현을 하면 스택 자체에는 각 정점이 무조건 1번씩 들어가지는 않고 여러 번 들어갈 수도 있지만 09번 줄의 처리로 인해 결국 연결된 정점을 보는 작업은 각 정점마다 최대 1번씩만 하기 때문에 시간복잡도는 동일하게 O(V+E)입니다. 만약 실수로 09번 줄을 빼먹는다면 연결된 정점을 보는 작업을 각 정점마다 여러 번 진행할 수 있기 때문에 코드의 시간복잡도가 굉장히 안좋아지거나 무한루프에 빠질 수 있습니다. 이런 경우 제출했을 때 시간 초과가 나거나 스택에 push가 계속 일어나서 메모리 초과가 발생할 수 있으니 조심해야 합니다.
다만 혹시 이전 슬라이드와 이번 슬라이드에서 다루는 내용이 잘 이해가지 않는다고 해도 너무 걱정할 필요는 없습니다. 어차피 코딩테스트 레벨에서는 그래프에서 꼭 DFS를 해야 할 일이 별로 없습니다. 그래프에서 DFS의 고유한 성질을 이용해야 하는 문제는 cycle detection, SCC, BCC, 오일러 경로 등과 같이 꽤 난이도가 있는 문제들이고 코딩테스트에서 이런 문제들을 볼 가능성은 거의 없다고 보시면 됩니다.

그러면 이제 문제를 풀어보겠습니다. 첫 번째 문제는 BOJ 11724번: 연결 요소의 개수 문제입니다. 이 문제는 진짜 너무 쉽고 힐링되지 않나요? 그래도 그래프 문제를 아예 처음 풀어보는거라 입력을 받는거에서 조금 실수를 할 수 있을 것 같습니다. 앞에서 배운 내용을 참고해서 한 번 짜보시고, 저는 BFS로 구현을 할거긴 한데 여러분들은 BFS도 해보고 재귀 DFS도 해보고 비재귀 DFS도 해보고 이것 저것 해보시면 좋겠습니다.

코드를 바로 같이 보면 앞에서 다 다룬 얘기여서 크게 설명할건 없어보입니다. 그래프가 양방향이니 16, 17번째 줄처럼 양쪽에 다 push_back을 해줘야 하고 BFS는 그냥 1926번 그림 문제와 비슷한 방법으로 돌면 끝입니다. (코드)

다음 문제는 BOJ 1260번: DFS와 BFS입니다. BFS는 그냥 구현을 하면 되지만 DFS는 비재귀 방식으로 구현을 할 경우 삐끗하면 방문 순서가 이상해질 수 있고 관련된 부분은 앞에서 설명을 충실하게 했기 때문에 앞의 내용을 참고해서 재귀 버전과 비재귀 버전 두 가지로 모두 구현해보는걸 추천드립니다. 앞에서 소개한 제 코드를 그냥 가져와서 그대로 쓰는게 꼭 나쁜건 아니지만 그보다는 내용만 참고하고 구현은 직접 해보시는걸 추천드립니다.

물론 저는 제 코드니까 그대로 가져왔습니다. 비재귀 DFS와 재귀 DFS를 다 담아서 코드가 조금 긴데, 아무튼 코드 자체는 앞에서 본 것과 같습니다. adj는 나중에 main 함수를 보면 알겠지만 정렬이 되어 있습니다. 그래서 비재귀 DFS에서는 21번째 줄처럼 스택의 특성상 역순으로 넣어야 작은 정점이 스택의 상단에 위치해서 작은 정점을 먼저 방문하게 됩니다.

다음으로 bfs 함수는 크게 설명할게 없고 main에서는 입력을 적절하게 잘 처리하고 각 adj에 대해 정점을 잘 정렬해둔 후에 dfs 함수와 bfs 함수를 차례로 호출하면 끝입니다. (코드)

이렇게 그래프를 배웠습니다. 그래프에서 활용되는 여러 알고리즘들은 뒤쪽에서 별도의 단원으로 배우게 될거고 일단 지금은 그래프의 표현법, 그리고 그래프에서 BFS와 DFS를 하는 방법 정도만 익혀두면 됩니다. 아마 문제들도 그렇게 막 어렵다는 느낌은 없이 다소 편안하게 풀 수 있을 것 같습니다. 그러면 고생 많으셨습니다.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x1B강 - 최소 신장 트리 (38) | 2022.01.08 |
|---|---|
| [실전 알고리즘] 0x1A강 - 위상 정렬 (12) | 2021.12.27 |
| [실전 알고리즘] 0x19강 - 트리 (25) | 2021.12.14 |
| [실전 알고리즘] 0x17강 - 우선순위 큐 (39) | 2021.11.22 |
| [실전 알고리즘] 0x16강 - 이진 검색 트리 (35) | 2021.11.06 |
| [실전 알고리즘] 0x15강 - 해시 (38) | 2021.09.27 |