문제 링크
https://programmers.co.kr/learn/courses/30/lessons/92343
예상 난이도
G3
알고리즘 분류
트리/DFS(or BFS)
풀이
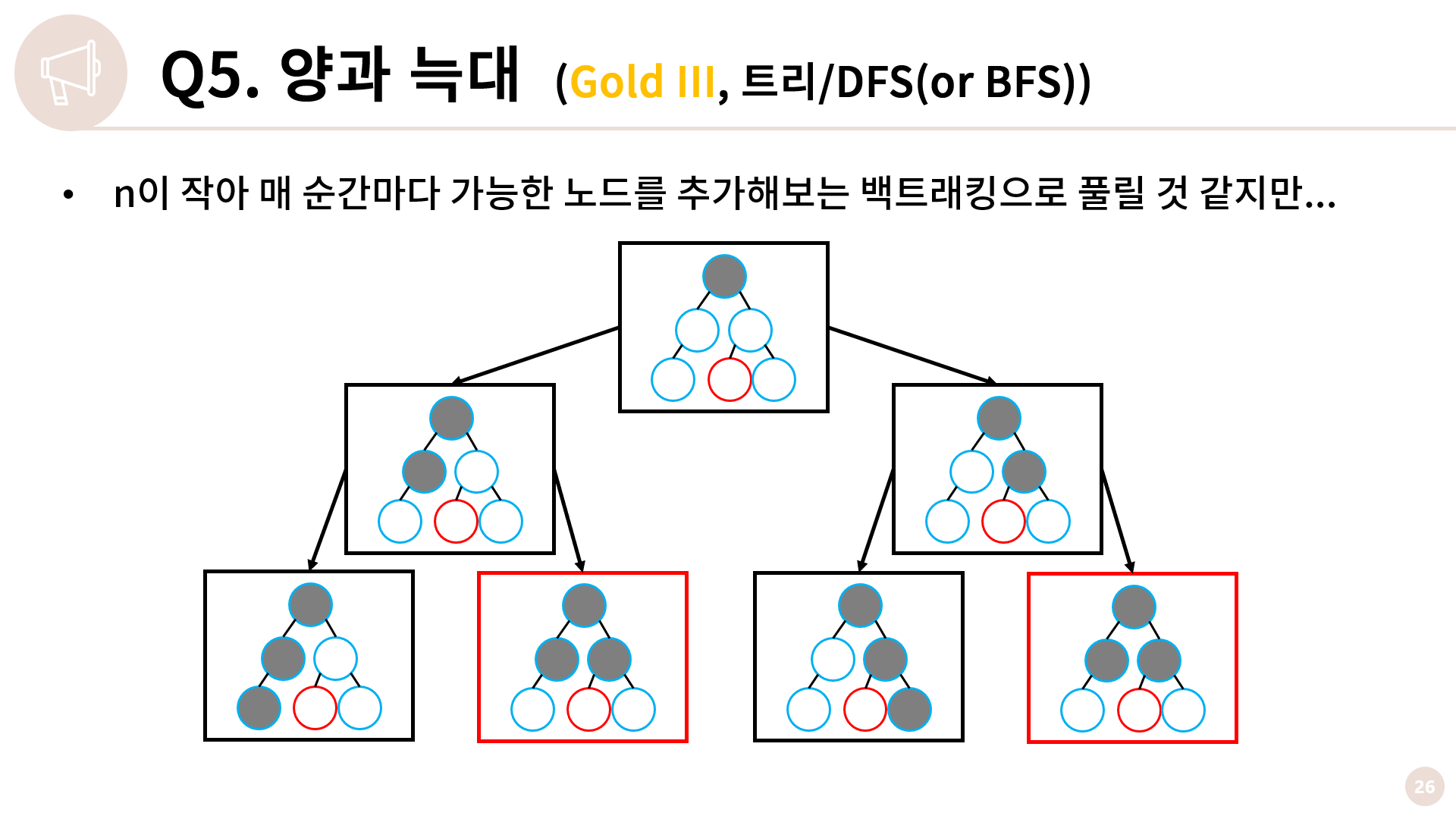
가장 쉽게 떠올릴 수 있는 풀이는 매 순간마다 가능한 노드를 추가해보는 백트래킹입니다. 그림에서 각 정점의 테두리 선 색은 파랑이 양을, 빨강이 늑대를 의미합니다. 그리고 회색으로 칠한 노드는 방문한 노드를 의미합니다. 처음 시작은 루트 노드만 방문한 상태이고 여기서 다음 상태는 왼쪽 자식을 방문하거나 오른쪽 자식을 방문한 상태입니다. 그리고 왼쪽 자식으로 내려갔다 치면 거기서 추가할 수 있는 다음 정점을 추가해 다음 단계로 넘어가고 뭐 이런 백트래킹 방법을 떠올릴 수 있습니다. 만약 이 백트래킹 풀이 자체가 잘 가닥이 잡히지 않는다면 아직 이 문제를 해결하기엔 배경 지식이 부족한 것으로 보이니 재귀와 백트래킹을 공부한 후 돌아오시는걸 추천드립니다.
그런데 이 백트래킹 풀이는 문제가 있습니다. 빨간색 네모로 표시된 저 두 그래프가 의미하는 바가 무엇일지, 왜 문제가 있다고 얘기를 하는건지 고민해봅시다. 힌트를 드리자면 피보나치 수열을 재귀로 구현할 때 시간복잡도가 산으로 간 이유를 다시 떠올려보세요.
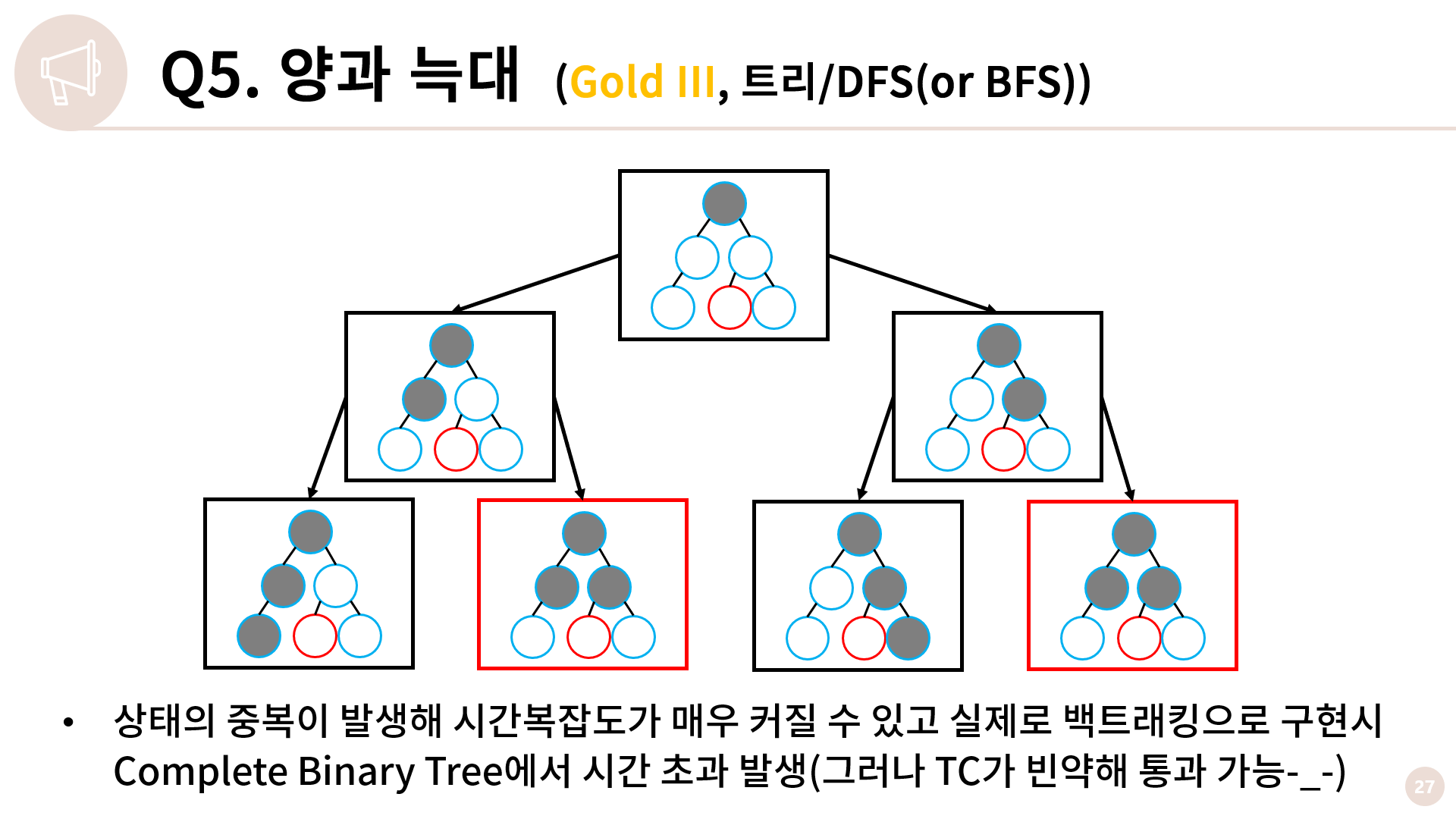
피보나치 수열을 재귀로 구현할 때 그러했듯 그냥 백트래킹을 돌려버리면 상태의 중복이 발생합니다. 그래서 시간복잡도를 가늠하기가 힘들고 또 실제로 백트래킹으로 구현을 해보면 Complete Binary Tree 형태에서 시간 초과가 발생합니다. 그런데 TC가 빈약한 탓에 백트래킹으로 구현을 해도 통과가 가능합니다.
(info = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
edges = [[0, 1], [0, 2], [1, 3], [1, 4], [2, 5], [2, 6], [3, 7], [3, 8], [4, 9], [4, 10], [5, 11], [5, 12], [6, 13], [6, 14], [7, 15], [7, 16]]
Return = 17 이 TC를 넣어보면 백트래킹 구현이 시간초과가 나는 것을 확인 가능)
이 문제도 그렇고 제가 풀이를 작성한 2021 카카오 채용연계형 인턴십, 2021 블라인드에서도 모두 원래는 시간초과가 발생해야 할 코드가 통과되는 문제가 하나씩 있었습니다. 즉 최근에 카카오에서 준비한 3번의 시험에서 TC가 빈약했던 문제가 있었네요. 올바른 풀이가 통과되지 않는 일이 발생하면 그건 정말 대참사이고 잘못된 풀이가 통과되는 일은 그보다는 임팩트가 살짝 낮긴 하지만, 그럼에도 불구하고 예를 들어 이 문제에서 시간복잡도를 고려하지 않고 백트래킹으로 구현을 해서 넘어간 사람보다 백트래킹 풀이를 생각했지만 앞에서 살펴본 것과 같은 분석을 통해 백트래킹은 시간 초과가 발생하겠다는걸 깨닫고 다른 방법을 찾다가 풀이를 떠올리지 못해서 제출을 못한 사람이 더 낮은 점수를 받는 상황은 바람직하지 않습니다. 이런 일이 계속 발생하는건 주최측의 신뢰도를 스스로 깎아먹을 수 밖에 없는 일이라고 생각합니다. 더군다나 그냥 TC가 빈약했던 이전 문제들과 달리 이 문제는 공식 해설에서조차 백트래킹으로 해결하는 잘못된 풀이를 제공하고 있다는 점에서 더 상황이 심각해보입니다.
물론 사실 이런 일은 비단 카카오뿐만 아니라 다른 기업의 코딩테스트에서도 비일비재한 일인데 다만 카카오는 문제를 공개하고 또 채점도 가능하게 두기 때문에 더욱 눈에 잘 띄는 것 뿐이라고 생각합니다. 하지만 어찌됐든 내부 출제 프로세스를 개선하고 검증을 더 꼼꼼하게 진행하면 좋겠습니다.

다시 본론으로 돌아와서, 상태의 중복으로 인해 시간복잡도가 산으로 가버리는 상황을 해결하는 방법은 간단합니다. 피보나치 함수에서 메모이제이션을 도입한 것과 같이 비트마스킹 기법을 이용해 특정 상태를 방문했는지 저장하면 됩니다. 정점이 n개라고 하면 가능한 부분집합, 즉 총 상태는 2n개가 있고 이 상태의 방문을 BFS 혹은 DFS로 처리하면 됩니다.
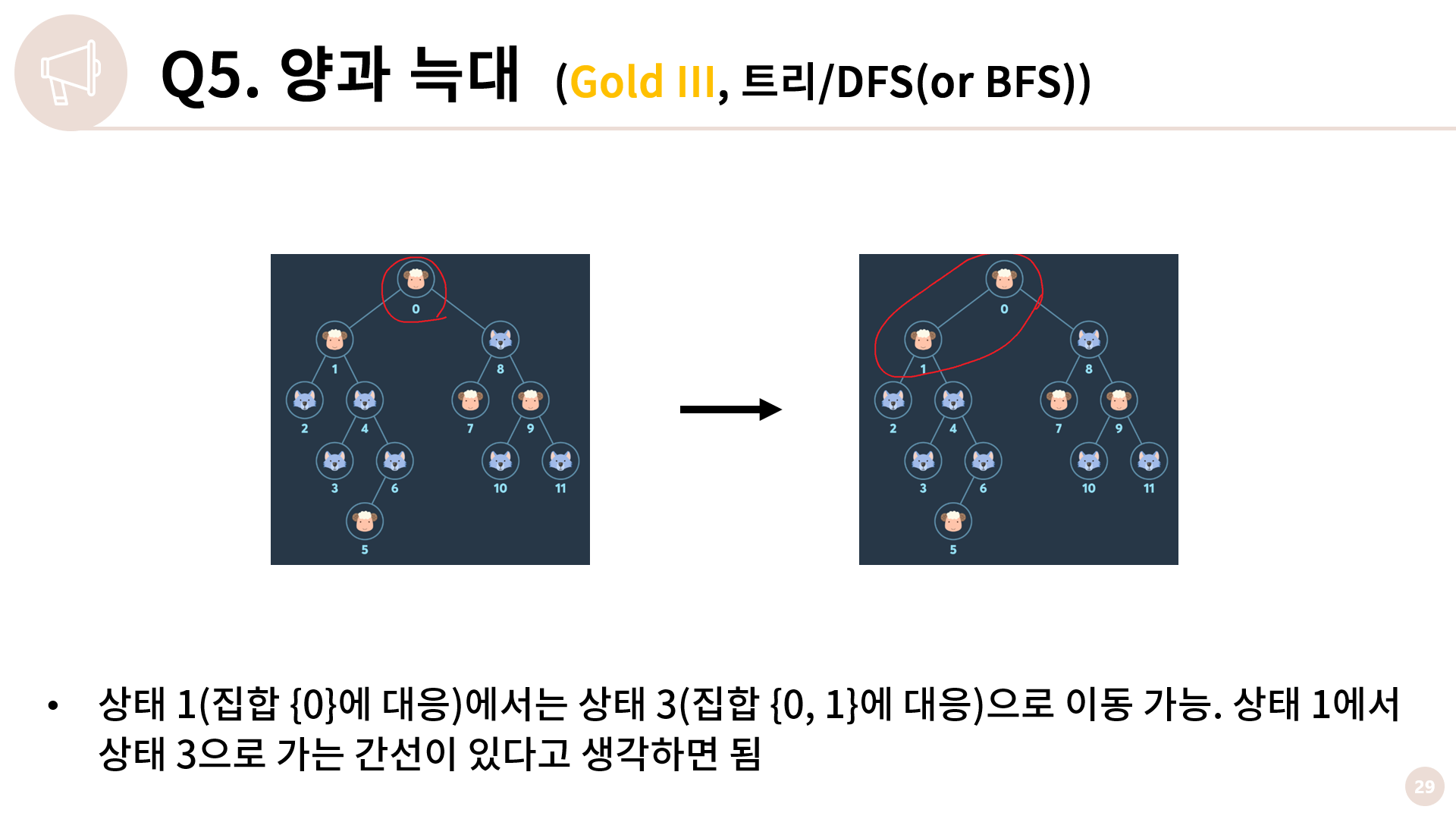
상태의 방문을 BFS 혹은 DFS로 처리하면 된다는게 무슨 소리인건가 좀 난해하게 느껴질 수 있을 것 같아 실제 예시로 설명을 드리겠습니다. 집합 {0}에서는 집합 {0, 1}로 넘어갈 수 있습니다. 집합 {0}은 비트마스킹을 하면 상태 1이고 집합 {0, 1}은 상태 3이니 상태 1에서 상태 3으로 가는 간선이 있다고 생각하면 됩니다.
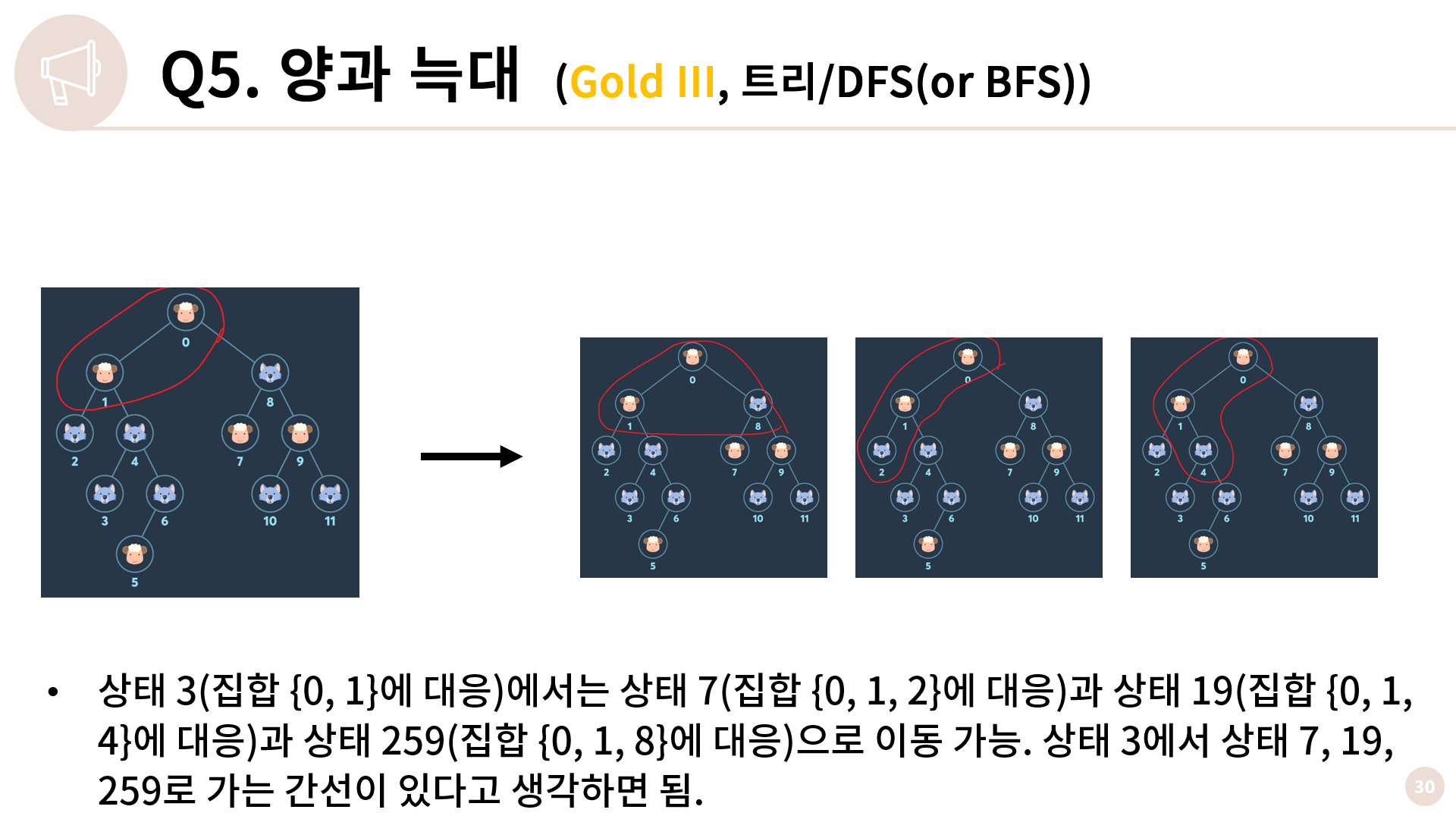
비슷하게 상태 3에서는 상태 7, 19, 259로 가는 간선이 있습니다. 이렇게 총 2n개의 각 상태를 정점으로 나타낸 새로운 그래프의 1번 정점(=상태 1)에서 Flood fill을 하고, 방문한 모든 상태에 대해서 양이 가장 많은게 몇 마리인지를 찾으면 됩니다.
'알고리즘 > Programmers' 카테고리의 다른 글
| [2022 KAKAO TECH INTERNSHIP] Q1. 성격 유형 검사하기 (C++, Python, Java) (0) | 2023.01.18 |
|---|---|
| [2022 KAKAO Blind Recruitment] Q7. 사라지는 발판 (C++, Python, Java) (17) | 2022.01.24 |
| [2022 KAKAO Blind Recruitment] Q6. 파괴되지 않은 건물 (C++, Python, Java) (1) | 2022.01.23 |
| [2022 KAKAO Blind Recruitment] Q4. 양궁 대회 (C++, Python, Java) (6) | 2022.01.20 |
| [2022 KAKAO Blind Recruitment] Q3. 주차 요금 계산 (C++, Python, Java) (0) | 2022.01.17 |
| [2022 KAKAO Blind Recruitment] Q2. k진수에서 소수 개수 구하기 (C++, Python, Java) (0) | 2022.01.17 |