
안녕하세요, 이번 시간부터 강의가 마칠 때 까지는 문자열 알고리즘을 다뤄보겠습니다. 미리 주의사항을 좀 알려드리자면 KMP의 경우 정말 헷갈립니다. 그렇기 때문에 이 강의를 보고 알듯말듯한 정도만 되면 성공이라고 생각하셔도 됩니다. 그리고 사실 KMP는 코딩테스트에 정말 드문 빈도로 나오는 알고리즘이라 나와도 기본 예제 수준으로만 나오지 응용을 필요로 하는 문제는 나올 가능성이 거의 없다고 볼 수 있는데, 뒤에서 다시 언급하겠지만 응용 없이 단순히 패턴 매칭만 필요하다면 g++에서는 strstr 함수가 KMP처럼 문자열과 패턴의 길이에 대한 선형 시간에 매칭 결과를 줘서 굳이 KMP를 몰라도 날로 먹을 수 있기도 합니다.
보통 학부 알고리즘 과목에서 KMP를 다루는 경우가 많아서 강의에 넣어두었지만 코딩테스트만 고려한다면 아예 응용까지 익힐게 아니고서는 굳이 KMP를 알아야 할 필요는 없습니다. 각자 상황에 맞춰서 내용을 취사선택하도록 합시다.

목차는 가볍게 보고 넘어가겠습니다.

KMP를 다루기 전에 이번 강의에서 사용할 용어들을 몇 가지 정의하고 가겠습니다. 첫 번째 줄과 같은 문자열의 slicing은 Python에서 사용하는 방식인데 본문에서 설명을 할 때도 저 표기가 간단해서 가져왔습니다. 혹시 Python을 이전에 배운 적 없어 S[a:b]라는 표현을 처음 보면 저기 적혀있는 정의를 잘 숙지해주세요. S[a]는 포함하지만 S[b]는 포함하지 않습니다.
|S|는 S의 길이를 의미합니다. 그리고 접두사와 접미사는 각각 문자열의 첫 문자를 포함하는 연속한 문자열, 문자열의 끝 문자를 포함하는 연속한 문자열을 의미합니다. slicing을 이용해 나타낸 정의도 한 번 이해해보도록 합시다.

이제 KMP 알고리즘이 무엇인지 알아봅시다. KMP 알고리즘은 문자열 A 안에 문자열 B가 들어있는지를 판단하는 알고리즘입니다. 일단 KMP 알고리즘을 모르는 상황에서 A 안에 B가 있는지를 확인하려면 어떻게 해야할까요?

구현하는 방법은 간단합니다. A의 각 위치별로 확인을 하면 됩니다. 먼저 A의 제일 앞부분이 B와 일치하는지 확인하는데 맨 첫글자부터 다릅니다.

A의 2번째 글자부터 확인했는데 또 다릅니다.

3번째도 다릅니다. 뒤는 설명 없이 쭉 보여드리겠습니다.





찾았습니다. A 안에는 B가 있었습니다. 이런 식으로 구현을 하면 됩니다. 강의를 지금까지 들어왔다면 이 정도는 당연히 구현을 할 수 있겠지만 그래도 제 코드를 한 번 보여드리겠습니다.

02번째 줄에서 (int)로 형변환을 하지 않으면 size 멤버 함수가 unsigned int 자료형이기 때문에 개판이 날 수 있다는건 늘 주의를 해주어야 하고 그 외에 딱히 코드에서 설명이 필요한 부분은 없어보입니다.
이 방법은 단순하면서도 일반적인 상황에서 매우 효율적으로 동작하기 때문에 보통 각 언어에서 패턴 매칭 문제를 해결하는 내장 함수는 이런식으로 구현이 되어있습니다. 물론 여기서 약간의 휴리스틱이 들어가있을 수는 있습니다. 그런데 이 구현의 시간복잡도는 최악의 경우 얼마일까요? 시간복잡도가 최악이 되는 A, B 모양을 고민해봅시다. 비단 지금뿐만 아니라 다른 상황에서도 본인의 코드에 대해 최악의 경우를 고민해보는건 코드의 시간복잡도를 분석할 때에도, 반례를 잡아낼 때에도 아주 큰 도움이 됩니다.

지금 이 예시가 최악의 예시입니다.

끝까지 가고 나서야 일치하지 않음을 알게되고

한 칸 옮겨서도 마찬가지고

끝날때까지 쭉 그렇습니다. 즉 최악의 경우 O(|A| × |B|)에 동작합니다. 이렇게 O(|A| × |B|)에 동작하는건 지금처럼 사실상 의도적으로 만든 매우 특수한 입력에서 벌어지는 일이고 일반적인 상황에서는 매 위치마다 O(|B|)에 걸쳐 비교를 하는 일이 잘 생기지 않지만 잘 아시다시피 알고리즘 문제에서는 가장 시간이 오래 걸리는, 즉 최악의 경우를 고려해야 하기 때문에 이를테면 A, B의 길이가 각각 최대 100만인 것과 같이 특수한 경우에서는 지금의 방법으로 해결을 할 수가 없습니다.

그러면 KMP 알고리즘이 뭐냐고 했을 때 KMP 알고리즘은 패턴 매칭 문제를 O(|A| + |B|)에 해결할 수 있게 해주는 기적의 알고리즘입니다. 그리고 KMP로 검색해서 다른 블로그들을 확인해보시면 알겠지만 공통적으로 적혀있는 얘기가 KMP는 굉장히 이해하기 어렵고 또 헷갈린다는 얘기입니다. 이번에 강의 자료를 만들면서도 어떻게 해야 보는 사람에게 이해를 잘 시킬 수 있을까 아주 고민을 많이 했습니다.

KMP 알고리즘을 이해하기에 앞서 KMP에서 쓰이는 실패함수를 알면 KMP를 이해하는데 도움이 됩니다.
일단 실패 함수 F(x)는 문자열 S[0:x+1]에서 자기 자신을 제외하고 접두사와 접미사가 일치하는 최대 길이로 정의됩니다. 뭔소린지 이해가 안가면 그거 당신 잘못 아닙니다. 아 물론 제 잘못도 아닙니다. 그냥 그럴 수 있습니다. 저도 언제였는지 솔직히 기억은 안나지만 아무튼 KMP를 처음 배울 때 말 그대로 뇌정지가 심하게 왔었습니다. 예시를 통해 이해를 하실 수 있도록 최대한 친절하게 예시를 구성했으니 같이 봅시다.
F(2)를 같이 구해볼건데, F(2)는 S[0:3]에서 자기 자신을 제외하고 접두사와 접미사가 일치하는 최대 길이입니다. 이말인즉슨 앞 3글자인 ABA에서 접두사와 접미사가 일치하는 최대 길이를 구하겠다는 의미입니다. F(x)가 문자열 S의 앞 x글자가 아니라 앞 x+1글자에서 접두사와 접미사의 최대 일치 길이라는 점을 꼭 기억해주세요. 먼저 F(2)가 2인지를 확인하려면 ABA에서 길이가 2인 접두사 AB와 접미사 BA가 일치하는지를 봅니다. AB와 BA는 다르기 때문에 F(2)는 2가 아닙니다.

다음으로 F(2) = 1인지 확인해보면 ABA에서 길이가 1인 접두사는 A이고 접미사도 A이어서 F(2)는 1입니다. 최대 길이를 구하고 싶기 때문에 지금 한 것과 같이 2부터 차례로 시도해봐야겠죠.

그러면 이 실패함수를 어떻게 구하는걸까요? 사실 아직 실패함수가 왜 필요한지조차 제대로 다루지 않았지만 그건 천천히 이해하는 것으로 합시다.
현재 저희가 시도할 수 있는 가장 쉬운 방법은 예를 들어 F(5)을 구하고 싶다고 할 때 F(5) = 5인지 확인하고, 일치하지 않으면 F(5) = 4인지 확인하고, 이렇게 하나하나 확인하는 방법입니다. F(5) = 5인지 확인해보면 ABABCA에서 길이가 5인 접두사 ABABC와 접미사 BABCA가 일치하는지를 봅니다. ABABC와 BABCA는 다르기 때문에 F(5)는 5가 아닙니다.

F(5) = 4인지 확인해보면 비슷한 분석을 통해서 F(5)은 4가 아님을 알 수 있습니다. 앞 두 글자는 같았는데 약간 아깝네요. 이 뒤는 설명없이 바로 보여드리겠습니다.



이렇게 F(5)가 1인지까지 쭉 확인을 해서 F(5) = 1임을 알게 되었습니다. 이런 식으로 계산을 하면 각 F(x)에 대해 최악의 경우 O(|S|^2)의 연산이 필요하기 때문에 시간복잡도는 O(|S|^3)입니다. 그런데 전체 F를 무려 O(|S|)에 구하는 방법이 있습니다. 전혀 감이 안오시겠지만 같이 알아보겠습니다.
전체 F를 O(|S|^3)가 아닌 O(|S|)에 구하려면 마치 다이나믹 프로그래밍과 같이 각 F의 값을 구할 때 이전의 F 값을 활용할 수 있어야 합니다. 일단 F(5)는 앞에서 같이 계산한 것 처럼 1임을 알고 있습니다. 이 상황에서 F(6)를 어떻게 구할 수 있는지 같이 고민해보겠습니다.

지금 이 그림에서 F(6)를 계산할 때 F(5)을 어떻게 이용할 수 있는지를 표시해뒀습니다. F(6)을 구할 때 이전에 하던 것 처럼 F(6) = 6인지, F(6) = 5인지 차례로 확인할 필요가 없고 F(5)가 1이라는 정보를 그대로 가져올 수 있습니다. 그렇게 되면 밑의 문자열을 움직일 필요가 없이 위와 아래 각각에서 이전에 확인한 문자열들의 다음 칸에 해당하는 두 글자가 일치하는지 확인하면 됩니다. 그 두 글자는 그림에 연한 초록과 진한 초록으로 표시해두었습니다. 두 글자가 B로 일치하기 때문에 최종적으로 접두사와 접미사의 앞 2글자가 같음을 알 수 있습니다. 이렇게 이전에 계산했던 정보를 재활용할 수 있습니다.

그런데 엄밀하게 말해서 F(5)로부터 F(6)에서 접두사와 접미사의 앞 2글자가 같다는건 알아냈지만 그렇다고 해서 F(6)을 2로 바로 확정지을 수는 없습니다. 2글자보다 더 많이 일치해서 F(6)이 2보다 클 수는 없는지를 확인해야 하기 때문입니다. 하지만 사실 논리적으로 생각해보면 F(5) = 1라는 사실로부터 F(6)이 2보다 클 수 없다는건 자동으로 따라오게 됩니다. 왜 그런지를 같이 살펴보겠습니다.

S에 A나 B 같은 글자가 적혀있으면 오히려 혼동을 줄 수 있어서 글자를 빼놓고 설명을 진행해보겠습니다. 우리는 F(6)이 2보다 클 수 없다는걸 귀류법으로 보이려고 합니다. 만약 F(6)이 2보다 크다면 적어도 S[0:7]에서 앞 3글자와 뒷 3글자가 일치한다는 의미니까 위의 그림과 같이 S[0:3] = S[4:7]입니다. 그런데 그렇게 되면 S[0:2]와 S[4:6]이 일치하기 때문에 F(5)가 최소 2 이상입니다. 이미 F(5) = 1이라는 사실을 알고 있기 때문에 F(5)가 최소 2 이상인 상황은 분명히 모순입니다. 그렇기 때문에 F(6)이 2보다 클 수는 없고, 최종적으로 F(6) = 2임을 알 수 있습니다.
지금까지 한 얘기를 일반화하면 우리는 F(k)을 구할 때 F(k-1)의 값을 이용할 수 있는데, F(k)은 최대 F(k-1)+1입니다. 그렇기 때문에 지금 이 예시처럼 만약 S[F(k-1)]와 S[k]을 비교해서 두 글자가 일치한다면 바로 F(k) = F(k-1) + 1로 확정지을 수 있습니다. 한편 F(k)을 구할 때 왜 S[F(k-1)]와 S[k] 이 두 글자를 비교하는지 약간 헷갈릴 수 있습니다. 이런 인덱스 문제가 사실 매번 굉장히 사람을 헷갈리게 만드는 요소이긴 하지만 특히 KMP를 구현할 때 이걸 잘 이해해야 코드를 받아들이기 쉬워서 같이 살펴보겠습니다.

일단 F(k)를 구하는 과정을 보면 이런식으로 일치하는 구간을 찾게 되고, 각 칸의 인덱스는 위에 적힌 것과 같습니다.

이 상황에서 윗쪽과 아랫쪽을 둘 다 한 칸씩 늘리면 인덱스가 각각 k와 F(k-1)이 되어서 결론적으로 S[F(k-1)]과 S[k]를 비교하면 됩니다.

이 관찰을 통해 F 배열을 처음부터 쭉 채워봅시다. 사실 지금 S[F(k-1)]과 S[k]가 일치하지 않을 때에 대해서는 알려드리지 않았는데, 조금 있다가 적절한 예시가 나오면 같이 살펴보도록 하겠습니다.
먼저 F(0)은 F의 정의상 S[0:1] = "A"에서 접두사와 접미사가 일치하는 최대 길이이니 자명하게 0입니다.

그 다음 F(1)도 계산해보면 "AB"에서 접두사와 접미사가 일치하는 최대 길이가 없어서 0입니다. S[F(0)] = S[0]과 S[1]을 비교해보면 둘의 값이 달라서 원래는 뭔가 다른 조치가 필요합니다. 하지만 예시가 별로 예쁘지 않아서 여기까지는 그냥 그런가보다 하고 생각하고 넘어가주세요.

F(2)를 구하기 위해서 S[F(1)] = S[0]과 S[2]를 비교해보면 둘은 일치합니다. 그러면 그전의 F 값인 F(1) = 0에서 뒤에 한 글자가 붙는게 F(2)이고, 그말인즉슨 F(2) = F[1] + 1입니다.

다음으로 F(3)을 구할땐 F(2)의 결과에서 글자 1개씩을 붙일 수 있는지 봅니다. S[F(2)] = S[1]과 S[3]을 비교해보면 둘은 일치하기 때문에 F(3) = F(2) + 1 = 2입니다.

이런 식으로 F의 마지막 값은 제외하고 다 채워두었다고 해봅시다. 드디어 마지막 칸을 채울 차례입니다.

만약 S[F(8)] = S[4]와 S[9]가 일치했다면 F(9) = F(8) + 1 = 5였겠지만 아쉽게도 두 글자가 다릅니다. 그러면 우리는 F(9) 값을 찾기 위해 아래에 있는 문자열을 오른쪽으로 밀어야합니다. 한 칸씩 밀면서 확인을 하면 F(9)가 4인지, 3인지, 2인지, 1인지를 확인할 수 있습니다. 그런데 이 때 이미 구해놓은 값을 가지고 영리하게 밀 수 있다는게 실패 함수를 효율적으로 구하는 키 포인트입니다.

제가 영리하게 미는 과정을 이해하는데에 필요한 값들에 전부 초록색으로 표시해두었는데 아마 전혀 이해가 안가시겠죠? 정상입니다. 하지만 저는 꿋꿋이 설명을 할테니 행운을 빕니다. 한번 듣고 이해가 안가더라도 한 다섯번 곱씹어보면 이해가 될 수 있습니다. 자 일단 F(8) = 4이기 때문에 그 전에 접두사 4글자와 접미사 4글자는 일치하던 상태였습니다. 하지만 한 글자를 추가하려고 하니 두 글자가 달라서 불가능한 상황이었습니다.

이 상황에서 그냥 늘 하던대로 별 생각없이 아래에 있는 문자열을 한 칸 오른쪽으로 밀어서 F(9) = 4인지 비교를 할 수도 있긴 하지만

오히려 원래 문자열은 잠깐 제쳐두고 이렇게 2개를 놓고 보겠습니다. 또 여기서 F(8) = 4로부터 알고있는 정보를 같이 표시해보면, 그 중에서도 초록색으로 표시된 부분을 아주 정말 주의깊게 들여다보면 한 100명 중에 1명은 아하 하고 깨달음을 얻을수도 있습니다.

아직 전혀 깨달음이 오지 않은 나머지 분들을 위해 좀 더 설명을 해보겠습니다. 우리는 F(3) = 2임을 미리 알고 있습니다. 또 F(3) = 2가 의미하는 바는 바로 저기 오른쪽 위에 그림으로 표시한 부분입니다. 접두사와 접미사의 3글자가 겹치지는 않지만 2글자는 겹친다는 의미이죠.

그리고 여기에 집중해봅시다. 우리는 지금 상황에서 오른쪽으로 미는 행위가 F[4], 즉 앞 4글자에서 접두사와 접미사의 최대 일치하는 부분과 관련이 있음을 알 수 있습니다. 만약 한 칸만 밀게 될 경우 F(3) ≠ 3일 때에 겹치는 구간이 그대로 겹쳐집니다.

우리는 F(3) = 2라는걸 알고 있기 때문에 접두사와 접미사가 2칸 겹치도록 바로 아래의 문자열을 2칸 밀어버리면 됩니다.
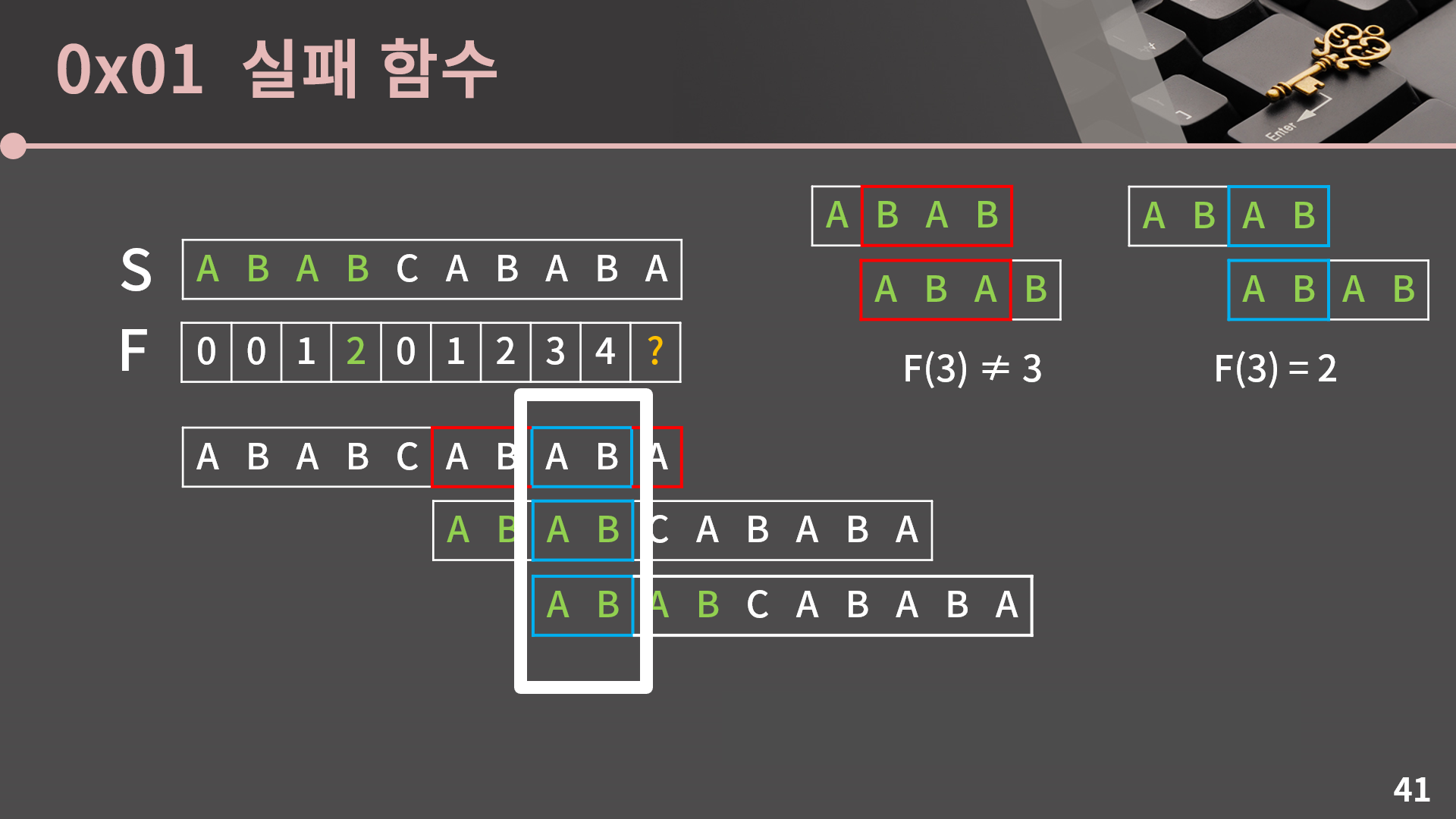
그리고 이렇게 2칸을 밀면 마지막 글자를 제외하고 나머지 글자는 자동으로 일치한다는 사실을 잘 이해하셔야 합니다. 첫 번째와 두 번째 문자열에서 해당 부분은 S[8] = 4였기 때문에 일치하고, 두 번째와 세 번째 문자열에서 해당 부분은 F(3)을 이용해 우리가 의도적으로 값이 동일하도록 밀었기 때문에 일치합니다.

마지막 글자를 제외한 나머지 부분의 값이 동일하다는걸 알고 있기 때문에 우리는 진한 초록과 연한 초록으로 표시한 마지막 글자만 확인하면 됩니다. 이 때 진한 초록은 S[9]이고, 연한 초록은 앞 4글자에서 접두사와 접미사의 최대 일치하는 부분의 한칸 뒤인 S[F(3)] = S[2]입니다. 이 둘은 A로 동일하기 때문에 최종적으로 F(9) = 3임을 알 수 있습니다.

지금까지 한 얘기를 다시 정리해보겠습니다. 기본적으로 현재의 F(i) 값을 구할 때에는 길이 F(i-1)만큼의 구간을 그대로 가져온 후 다음 한 글자가 일치하는지를 확인합니다. 만약 일치한다면 F(i) = F(i-1) + 1로 쉽게 계산됩니다.

하지만 그림과 같이 일치하지 않을 경우에는 아래의 문자열을 적절하게 밀어주어야 합니다. 그리고 여기서 얼마나 밀어줄지 결정하기 위해서 현재 겹친 영역(파란색 테두리 영역)에서 접두사와 접미사가 얼마나 겹쳤는지를 참고할 수 있습니다.

이렇게 이전에 일치하던 구간에서 접두사와 접미사가 겹치는 구간을 그대로 살려 아래의 문자열을 밀어준 후 마지막 글자를 비교하면 됩니다. 만약 여기서 각 마지막 글자가 다르다면 초록색 구간 안에서 접두사와 접미사가 얼마나 겹쳤는지를 확인해 그 구간을 그대로 살려 다시 아래의 문자열을 밀어주는걸 반복하면 됩니다.
이렇게 실패 함수에 대한 설명을 마쳤는데 아마 정말 심각하게 헷갈리고 혼란스러울 수 있습니다. 하지만 그것이 정상이니 나만 바보인건가 하고 생각할 필요는 없고, 심호흡을 크게한 뒤 잠시 맑은 공기를 마시고 다시 돌아옵시다.
이제 이것을 구현하는 아주 큰 고비가 남았습니다. 구현을 할 때에는 실제로 문자열을 미는게 아니라 위와 아래에서 비교를 해야 할 두 인덱스만 가지고 갑니다. 도식화해서 보여드린 실패 함수 계산 과정을 인덱스와 함께 다시 확인해봅시다.

먼저 i와 j를 각각 위와 아래의 인덱스라고 합시다. S[i]와 S[j]가 일치하는지를 비교하게 되는데, S[i] == S[j]일 경우 F[i] = j+1이고 i와 j를 모두 1 증가시키면 됩니다. 1-indexed, 0-indexed 등의 문제로 F(i) = j+1인지 F(i) = j인지 등이 굉장히 헷갈릴 수 있는데, F(x)의 정의가 문자열 S[0:x+1]에서 접두사와 접미사가 일치하는 최대 길이임을 다시 한 번 상기하면서 잘 이해해봅시다.

S[i] != S[j]일 경우에는 우선 j가 F(i-1)이고 초록색 영역의 길이가 F(j-1)임을 이해해야 합니다.

그렇게 되면 i는 그대로이고 j만 F(j-1)로 바뀜을 알 수 있습니다. 만약 여기에서 또 S[i]와 S[j]가 일치하지 않는다면 다시 j = F(j-1)로 바뀌게 됩니다. 지금까지 제 강의들에서는 동작 원리를 설명드리고 제 코드를 보여드리기 전에 먼저 구현을 해보시라고 권유를 하는 경우가 많았지만 이번 내용은 아무리 생각해도 이 설명만을 보고 동작 원리를 완벽히 이해해서 구현을 하는게 불가능에 가깝다고 생각을 하기 때문에 코드를 바로 보여드리겠습니다. 코드를 보고 아주 긴 시간동안 머리를 쥐어뜯으며 이해를 해보려고 노력해봅시다.

이 실패 함수 내용이 꽤 난해했는데 코드를 보면 당혹스러울 정도로 간결합니다. 간결하지만 하나하나 뜯어보면 앞에서 설명한 내용이 다 잘 들어가있습니다. 앞에서 말했던 것 처럼 인덱스 i는 위에서 비교가 이루어지는 문자열의 위치이고 인덱스 j는 아래에서 비교가 이루어지는 문자열의 위치입니다. f[i]를 구할 때에는 당연히 s[i]를 비교하게 되고 j는 비교를 하면서 옮겨다니게 됩니다. 05번째 줄의 while문이 많이 헷갈릴텐데, 일단 s[i]와 s[j]가 일치한다면 while문 안의 조건이 false이니 바로 06번째 줄로 가서 f[i] = ++j, 즉 j += 1 / f[i] = j 이 실행됩니다. s[i]와 s[j]가 일치하지 않는다면 while문에서 계속 붙잡혀있으면서 j = f[j-1]으로 바꿔나가는데 이게 앞에서 같이 살펴본 것 처럼 밑의 문자열을 적절하게 밀어주는 과정인거고 그러다가 j = 0이 되면 while문을 탈출하는 로직입니다.

드디어 KMP를 이해하기 위한 모든 준비가 끝났습니다. 실패 함수를 이해하는게 KMP 이해의 80% 이상을 차지하고 있기 때문에 실패 함수를 이해했다면 KMP는 사실상 거의 거저 따라온다고 생각하면 됩니다. 우리는 A 안에 B가 들어있는지 구하고 싶습니다. 그냥 정직하게 짜면 제일 앞에서 본 것 처럼 O(|A| × |B|)가 걸릴테지만 KMP 알고리즘을 통해 O(|A| + |B|)에 해결하고 싶습니다. 이 과정에서 B에 대한 실패 함수를 필요로 하는데, 실패 함수를 복습하는 차원에서 저 표를 채워봅시다.

표를 채우면서 실패 함수 과정을 잘 따라가보셨을거라고 생각합니다. 그리고 신기하게도 A에서 B를 찾는 KMP 자체가 실패 함수를 찾는 과정과 굉장히 유사합니다. 과정을 같이 확인해봅시다.

또 다시 i, j가 나옵니다. 이 i, j는 실패 함수와 같이 위(=A)와 아래(=B)에서 비교가 이루어지는 문자의 위치를 말합니다. 일단 처음엔 A[0]과 B[0]을 비교하고 둘은 일치합니다.

일치하니까 계속 가봅시다. 일단 당장은 왜 그런지 이유를 생각하지 마시고 그냥 설명을 따라와주세요. 실패 함수를 구할 때와 마찬가지라고 생각할 수 있는데, 밑의 문자열을 움직이지 말고 i와 j를 둘 다 1 늘려서 일치하는지 확인합니다. A[1]과 B[1]이 일치합니다. 이제 계속 일치하는 부분은 한번에 쭉 보여드리겠습니다.




잘 나가다가 i = 5, j = 5에서 두 글자의 불일치가 발생했습니다. 그러면 아래의 문자열을 옮겨야하는데 여기서 한 칸만 옮기면 기존의 비효율적인 방법과 다를게 없습니다. 여기서 아래의 문자열을 얼마만큼 오른쪽으로 옮기면 될지, 다른 말로 표현하면 j의 값을 얼마로 두면 될지 실패 함수를 구할 때 나왔던 비슷한 상황을 떠올리면서 알아맞춰봅시다.

저기 실패 함수의 값 중 하나에 주황색으로 칠을 해두었습니다. 저 F(4) = 3라는 값은 "ABABA"에서 접두사와 접미사가 일치하는 최대 길이가 3글자라는 의미입니다. 이제 뭔가 좀 보이시나요?

잠깐 문자열 A는 신경쓰지 말고 원래의 B와 실패 함수를 이용해 옮긴 B에만 집중을 해보겠습니다. 이전에 실패 함수에서 본 것과 같은 맥락인데 비록 지금 B[i]와 B[j]가 다르기 때문에 B를 옮겨야하지만 앞의 다른 글자들은 다 일치했으니 일치하는 구간을 최대한 살리고 싶습니다. 그렇기 때문에 "ABABA"에서 접미사와 접두사가 일치하는 3글자를 그대로 살리면서 아래의 문자열을 이동시키면 됩니다. 그런데 이 때 j의 값은 얼마일까요? 물론 눈으로 보면 3이란걸 알 수 있긴한데 이 3이라는 값은 어떻게 계산된 값일까요?

이 값은 F(j-1) = F(4)입니다. F(4)의 정의가 "ABABA"에서 접두사와 접미사가 일치하는 최대 길이였고, 우리는 일치하는 "ABA"의 다음 글자를 B[i]와 비교해야 하기 때문에 그렇습니다. 0-indexed, 1-indexed 등의 문제로 F(4)인지 F(4)+1인지 이런게 헷갈린다면 F의 정의나 앞에서 그림을 참고해서 확실히 바로 잡고 가는걸 추천드립니다.

그렇기 때문에 결론적으로 우리는 A[i]와 B[j]의 불일치가 발생하면 j를 F[j-1]로 옮기면 됩니다. 실패 함수를 구할 때 하던 방식과 동일합니다.

그리고 그 다음 비교를 이어가면 됩니다. A[5]과 B[3]이 일치합니다.

i, j를 모두 1 증가시킵니다. A[6]과 B[4]가 일치합니다.

i, j를 모두 1 증가시킵니다. 이번에는 A[7]과 B[5]가 일치하지 않습니다. j를 어떻게 옮겨야할지 알아맞춰봅시다.

첫 5글자에서 접미사와 접두사가 일치하는 최대 길이인 F(4)로 옮기면 됩니다. F(4)가 3이니 3개가 겹치는건 그대로 활용할 수 있고 A[i]와 B[j]를 비교해볼 차례입니다.

아쉽게도 글자가 일치하지 않습니다. 이러면 또 다시 j를 옮겨야하는데 어디로 옮겨야할까요?

첫 3글자에서 접미사와 접두사가 일치하는 최대 길이인 F(2)로 옮기면 됩니다.

하지만 이번에도 다음 글자가 일치하지 않았습니다. j를 다시 옮겨야 합니다.

j를 F(0)으로 옮기면 됩니다. 이제 다시 바닥에서 시작하는 느낌이네요. 그리고 여기서마저 글자가 일치하지 않습니다.

더 이상 j를 옮길 곳이 없으니 i를 1 증가시킵니다. 이번에는 A[i]와 B[j]가 일치하네요. 계속 하던대로 i와 j를 모두 1 증가시킵니다.

이번에도 일치합니다. 계속 쭉 일치하기 때문에 조금 생략을 하고 넘어가겠습니다.

이렇게 j가 8, 즉 끝에 도달하게 되면 A 안에 B가 있음을 확인할 수 있습니다. 만약 A 안에 B가 있는지 여부만을 확인하고 싶다면 여기서 탐색을 중단하면 되지만 B가 등장하는 횟수를 구하고 싶다거나, B가 등장하는 모든 위치를 구하고 싶다면 여기서 탐색을 계속 이어나가야 합니다. 그러면 이 때 j를 어떤 값으로 바꾸면 될지 고민해봅시다.

F(8)의 값을 참고해서 j를 3으로 옮기면 됩니다. 이후 A[i]와 B[j]를 비교한 후 다시 j를 옮기는 작업이 반복됩니다. 뒤의 작업은 생략하겠습니다.
이렇게 KMP 알고리즘의 전 과정을 알아보았습니다. KMP에서는 접미사와 접두사의 일치를 바탕으로 탐색을 효율적으로 수행합니다. 앞에서 본 실패 함수의 코드를 잘 이용해 구현을 직접 해보셔도 좋고, 아직 자신이 없으면 바로 코드를 확인하셔도 좋습니다. 구현을 해본 후에는 BOJ 16916번: 부분 문자열 문제에서 제대로 구현을 했는지 확인할 수 있습니다.

실패 함수 부분은 그대로 가져왔습니다. 그리고 21번째 줄부터 시작하는 for문 안에서 i와 j의 움직임을 처리하는데 실패 함수에서 보던 로직과 굉장히 유사함을 확인할 수 있습니다. 만약 24번째 줄과 같이 j가 p.size()에 도달하면 문자열 s 안에 문자열 p가 있음을 확인할 수 있는데, 이 문제에서는 부분 문자열 여부만을 판단하기에 여기서 바로 1을 출력하고 종료했습니다. 만약 탐색을 계속 이어가고자 할 경우에는 이 부분이 어떻게 바뀌어야 하는지 고민을 해보시는 것을 추천드립니다. 당장 문제집에 있는 문제 중 이런 고민이 필요한 문제가 있습니다. 그리고 정답을 받은 후 다른 분들의 코드를 보시면 알겠지만 사실 채점 서버 기준(=g++ 기준) strstr 함수가 선형 시간에 동작하기 때문에 지금처럼 그냥 단순하게 등장 여부만을 선형 시간에 확인해야할 경우에는 그냥 strstr 함수를 써서 날로 먹을 수 있긴 합니다. 하지만 등장하는 횟수를 구해야 한다거나, 아예 실패 함수를 가지고 뭔가 응용이 들어가면 단순히 strstr함수로는 해결이 힘들고 KMP가 필요하게 됩니다.

이렇게 KMP 알고리즘을 알아보았습니다. 많이 어려운 내용이고 특히 이 알고리즘을 이번에 처음 접했을 경우 이해가 잘 가지 않는 것이 정상입니다. 이해를 위해 다른 사람들의 자료를 찾아보셔도 괜찮은데, F나 문자열의 인덱스 등이 제 강의에서 정의한 것과 다를 수 있기 때문에 이를 유의할 필요가 있습니다.
KMP는 코딩테스트 기준 그렇게까지 비중이 있는 내용은 아니기 때문에 도저히 이해가 안간다면 여기에 온 시간을 쏟기 보다는 다른 단원의 내용을 학습하는게 더 의미있을 수 있습니다.
한편 KMP에는 실패 함수를 이용하거나 기타 등등 다양한 응용법이 존재합니다. 해당 문제들을 응용 문제로 두긴 했지만 난이도가 꽤 높기 때문에 대회를 노리는게 아니라면 굳이 학습할 필요는 없어 보입니다. 그러면 고생 많으셨습니다.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 부록 B - 동적 배열 (13) | 2024.01.27 |
|---|---|
| [실전 알고리즘] 부록 A - 문자열 기초 (18) | 2023.05.03 |
| [실전 알고리즘] 0x1F강 - 트라이 (48) | 2022.09.06 |
| [실전 알고리즘] 0x1D강 - 다익스트라 알고리즘 (49) | 2022.02.19 |
| [실전 알고리즘] 0x1C강 - 플로이드 알고리즘 (17) | 2022.02.09 |
| [실전 알고리즘] 0x1B강 - 최소 신장 트리 (38) | 2022.01.08 |