2022. 3. 27. 14:25, CTF/Crypto
Vulnerability is quite simple(nonce reuse in GCM mode) but I was struggled with TCP packet structure. I am newbie in network...
I confused that GCM mode is affected on Application data but it wasn't. It is related with PSK Identity field(I realized this by searching aa aa aa aa / bb bb bb bb hex data)

There are three PSK Identity field data, and IV is collide.
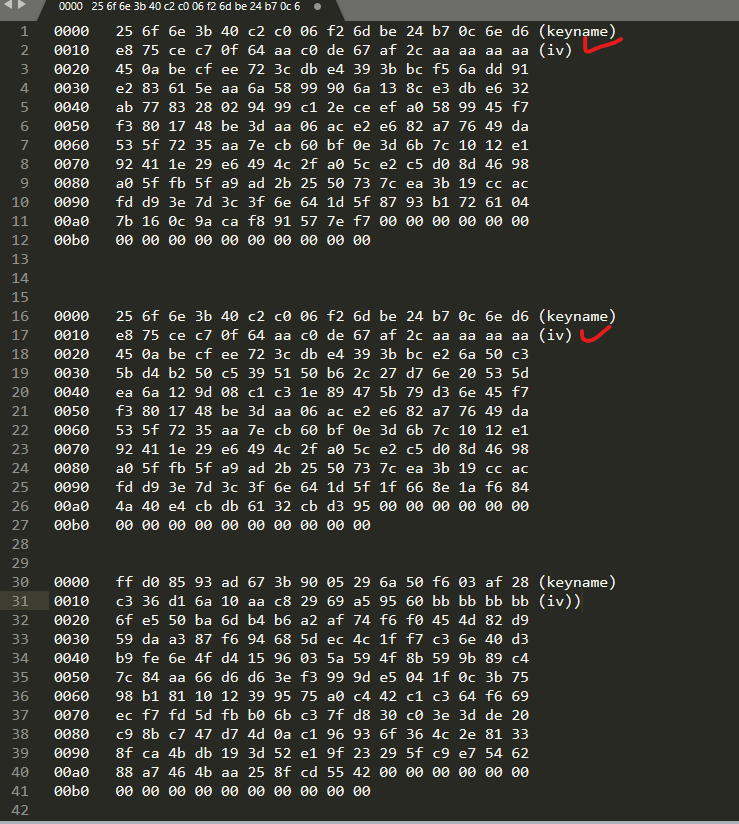
First two data are encrypted using $key0$, last one is encrypted using $key1$. It is known that single nonce collision in GCM break downs all. Moreover, $H = AES_K(0^n)$ is revealed by solving univariate equation in GF field. Since $key1 = AES_{key0}(0^n) = H$, everything is clear. I know that below code is ugly and I will refactor someday😅
solver.sage
from binascii import unhexlify, hexlify
import hashlib
from Crypto.Cipher import AES
def slice_and_pad(b_str, bsize=16):
rem = (bsize - len(b_str) % bsize) % bsize
b_str += b"\x00" * rem
return [bytearray(b_str[k:k+bsize]) for k in range(0, len(b_str), bsize)]
def unhex_blocks(h_str, bsize=16):
h_str = unhexlify(h_str)
return slice_and_pad(h_str, bsize)
def xor(a, b):
assert(len(a) == len(b))
return bytearray([a[i] ^^ b[i] for i in range((len(a)))])
def byte_to_bin(byte):
b = bin(byte)[2:]
return "0" * (8 - len(b)) + b
def block_to_bin(block):
assert(len(block) == 16)
b = ""
for byte in block:
b += byte_to_bin(byte)
return b
def bytes_to_poly(block, a):
f = 0
for e, bit in enumerate(block_to_bin(block)):
f += int(bit) * a**e
return f
def poly_to_int(poly):
a = 0
for i, bit in enumerate(poly._vector_()):
a |= int(bit) << (127 - i)
return a
def poly_to_hex(poly):
return (hex(poly_to_int(poly))[2:])
def GCM_poly(COEF, L_p, C_p, A_p):
return COEF + L_p * X + sum(C_p[i] * X**(len(C_p)+1-i) for i in range(len(C_p))) + sum(A_p[i] * X**(len(C_p)+len(A_p)+1-i) for i in range(len(A_p)))
# C & AAD are hexstring(i.e. "11223344")
def forge_message(enc_J0_p, H_p, C, AAD, A_p):
L = unhex_blocks(hex(((int)(160 << 64) | (len(C)*4)))[2:].zfill(32))[0]
L_p = bytes_to_poly(L, a)
C_block = unhex_blocks(C)
C_p = [bytes_to_poly(elem, a) for elem in C_block]
T = poly_to_hex(GCM_poly(enc_J0_p, L_p, C_p, A_p)(H_p))
msg = AAD + C + T
return msg
# packet 4
dat1 = '256f6e3b40c2c006f26dbe24b70c6ed6e875cec70f64aac0de67af2caaaaaaaa450abecfee723cdbe4393bbcf56add91e283615eaa6a5899906a138ce3dbe632ab778328029499c12eceefa0589945f7f3801748be3daa06ace2e682a77649da535f7235aa7ecb60bf0e3d6b7c1012e192411e29e6494c2fa05ce2c5d08d4698a05ffb5fa9ad2b2550737cea3b19ccacfdd93e7d3c3f6e641d5f8793b17261047b160c9acaf891577ef7'
C1 = unhex_blocks(dat1[64:-32])
T1 = unhex_blocks(dat1[-32:])
A1 = unhex_blocks(dat1[:64])
L1 = unhex_blocks(hex(((int)(256 << 64) | 976))[2:].zfill(32))
# packet 10
dat2 = '256f6e3b40c2c006f26dbe24b70c6ed6e875cec70f64aac0de67af2caaaaaaaa450abecfee723cdbe4393bbce26a50c35bd4b250c5395150b62c27d76e20535dea6a129d08c1c31e89475b79d36e45f7f3801748be3daa06ace2e682a77649da535f7235aa7ecb60bf0e3d6b7c1012e192411e29e6494c2fa05ce2c5d08d4698a05ffb5fa9ad2b2550737cea3b19ccacfdd93e7d3c3f6e641d5f1f668e1af6844a40e4cbdb6132cbd395'
C2 = unhex_blocks(dat2[64:-32])
T2 = unhex_blocks(dat2[-32:])
A2 = unhex_blocks(dat2[:64])
L2 = unhex_blocks(hex(((int)(256 << 64) | 976))[2:].zfill(32))
F, a = GF(2**128, name="a").objgen()
R, X = PolynomialRing(F, name="X").objgen()
A1_p = [bytes_to_poly(elem, a) for elem in A1]
C1_p = [bytes_to_poly(elem, a) for elem in C1]
T1_p = [bytes_to_poly(elem, a) for elem in T1]
L1_p = [bytes_to_poly(elem, a) for elem in L1]
A2_p = [bytes_to_poly(elem, a) for elem in A2]
C2_p = [bytes_to_poly(elem, a) for elem in C2]
T2_p = [bytes_to_poly(elem, a) for elem in T2]
L2_p = [bytes_to_poly(elem, a) for elem in L2]
print(L1_p)
f1 = GCM_poly(T1_p[0], L1_p[0], C1_p, A1_p)
f2 = GCM_poly(T2_p[0], L2_p[0], C2_p, A2_p)
# 1. Recover H from iv reuse
p1 = f1 + f2
# only one candidate
for root, _ in p1.roots():
H_p = root
if H_p == 0: continue
H = poly_to_hex(H_p)
print("H", H)
break
# 2. Recover key1
key1 = hashlib.sha256(bytes.fromhex(H)).digest()
# 3. Extract keyname, aeskey
dat3 = 'ffd08593ad673b9005296a50f603af28c336d16a10aac82969a59560bbbbbbbb6fe550ba6db4b6a2af74f6f0454d82d959daa387f694685dec4c1ff7c36e40d3b9fe6e4fd41596035a594f8b599b89c47c84aa66d6d63ef3999de5041f0c3b7598b1811012399575a0c442c1c364f669ecf7fd5dfbb06bc37fd830c03e3dde20c98bc747d74d0ac196936f364c2e81338fca4bdb193d52e19f23295fc9e7546288a7464baa258fcd5542'
C = bytes.fromhex(dat3[64:-32])
T = bytes.fromhex(dat3[-32:])
AAD = bytes.fromhex(dat3[:64])
iv = bytes.fromhex(dat3[32:32+24])
chk = hashlib.sha512(key1).digest()
keyname = chk[:16]
aeskey = chk[16:32]
assert(keyname == AAD[:16])
# 4. decrypt
cipher = AES.new(aeskey, AES.MODE_GCM, iv)
cipher.update(AAD)
plain_data = cipher.decrypt_and_verify(C, T)
print(plain_data)'CTF > Crypto' 카테고리의 다른 글
| [RCTF 2022] guess (2) | 2022.12.13 |
|---|---|
| [SECCON CTF 2022] janken vs kurenaif (0) | 2022.11.13 |
| [SECCON CTF 2022] this_is_not_lsb (0) | 2022.11.13 |
| [LINE CTF 2022] Forward-or (0) | 2022.03.27 |
| [LINE CTF 2022] X Factor (0) | 2022.03.27 |
| [LINE CTF 2022] ss-puzzle (0) | 2022.03.27 |
Comments