------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
현재 보고있는 강의는 구버전입니다. 내용에는 문제가 없으나 리뉴얼 중이니 이 게시글을 참고해주세요.
리뉴얼한 버전은 [실전 알고리즘] 0x19강 - 트리에서 확인할 수 있습니다. 리뉴얼 버전으로 보시는 것을 추천드립니다.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

이번 시간에는 트리를 다루어봅시다.


저희는 0x0D강에서 이진 검색 트리를 배우며 이미 "트리"라는 개념을 적당히 받아들였습니다.
당시에는 이런식으로 "꼭대기부터 아래까지 계층을 이루고 있고, 제일 꼭대기를 제외한 나머지 정점들은 위로 딱 1개와 연결이 되어있는 구조" 정도로만 받아들이고 넘어갔습니다.
그런데 이전 강의에서 배운 것도 있고 하니 잘 생각해보면 트리 또한 간선과 정점으로 이루어진 자료구조로, 그래프의 특별한 종류임을 알아차릴 수 있습니다.
이진 검색 트리때 소개했던 용어를 다시 한 번 정리하고 가겠습니다. 제일 꼭대기의 정점은 루트입니다.
간선으로 직접 연결된 상하 정점을 부모와 자식이라고 부릅니다.
자식이 없는 정점은 리프입니다. 그림에서는 총 4개의 리프가 있습니다.
그리고 루트와의 거리가 1인 정점은 Depth가 1이고, 2인 정점은 Depth가 2입니다. Depth가 1인 정점은 3개, 2인 정점은 2개, 3인 정점은 2개가 존재합니다.

그렇다면 이번에는 트리를 수학적으로(정확히는 그래프이론적으로) 깔끔하게 정의해볼 시간입니다.
기본적으로 단순 그래프(=루프가 없고 서로 다른 두 점을 연결하는 간선이 최대 1개인 그래프) 상황을 가정합니다. 이 때 트리는 무방향이면서 사이클이 없는 연결 그래프로 정의됩니다.
뭔가 깔끔해보이긴 하면서도 좀 아리송하고... 왜 앞에서 소개한 트리 모양이 늘 "무방향이면서 사이클이 없는 연결 그래프"인지 잘 와닿지 않을 수 있습니다. 이해를 돕기 위해 첨언하자면 저희가 느낌적으로 알고 있는 "트리"라는 것이 연결 그래프이어야 함은 자명합니다. 또한 간선의 방향성은 없다고 칩시다. 그러면 남은 것이 "사이클이 없다"라는 부분일텐데, 사이클이 있을 경우 지금 그림에서 점선 모양의 간선이 추가되는 것 마냥 뭔가 트리 모양이 이상해져서 트리가 아니게 된다 정도로만 받아들이고 넘어가시면 되겠습니다.
굳이 증명이 필요하다면 계층 구조로서의 트리를 귀납적으로 정의한 후 귀납법을 통해 증명을 할 수는 있지만 불필요하다고 생각이 들어 생략하겠습니다.

트리의 수학적인 정의로부터 이 슬라이드에서 제시된 다양한 그래프들이 전부 트리임을 알 수 있습니다.
앞에서 이진 탐색 트리를 다룰 땐 계층적인 구조로서의 트리를 다루었지만 트리의 정의 상으로는 계층과 관계된 것이 없으며, 또 정점이 1개이고 간선이 없는 그래프도 트리임에 유의해야 합니다.

트리의 정의는 아래의 명제들과 동치입니다. 명제들은 모두 무방향 단순 그래프임을 가정합니다.
다양한 명제들이 있지만 모두를 외울 필요는 없고, 머릿속으로 한 번만 생각을 해보고 넘어가면 됩니다. 단 $V$개의 정점을 가진 트리는 $V-1$개의 간선을 가지고 있다는 성질과 임의의 두 점은 연결하는 simple path가 유일하다는 것은 기억해두는 것이 좋습니다.

트리에서는 임의의 노드를 루트로 만들 수 있습니다. 트리가 마치 구슬과 실로 연결되어 있다고 생각할 때 아무 구슬 하나를 잡고 위로 올린 상황이라고 생각해도 됩니다. 주어진 6개의 트리는 모두 같은 트리입니다.
트리에서 루트가 정해지고 나면 루트는 부모가 없고 나머지 모든 노드의 부모가 1개로 고정됩니다. 단, 루트가 달라지면 각 노드의 부모 또한 달라집니다. 예를 들어 1이 루트일 때는 2의 부모가 1이었지만 4가 루트일 땐 2의 부모가 4로 바뀌었습니다.

트리에서의 BFS와 DFS에 대해 알아보겠습니다.
기본적으로 트리는 그래프의 특별한 한 종류이기 때문에 이전 장에서 배운 BFS, DFS 알고리즘을 그대로 적용시킬 수 있습니다.
우선 BFS의 경우 임의의 시작점을 잡고 BFS를 돌리면 그 시작점을 루트로 정해서 트리를 재배치했을 때의 높이 순으로 방문을 하게 됩니다. 그림에서 1번 정점을 시작점으로 잡고 BFS를 돌리면 1, 2, 3, 4, 5, 6, 7, 8 순으로 방문을 하게 됩니다. 물론 큐에 무엇을 먼저 넣는지에 따라 (2, 3, 4), (5, 6), (7, 8) 사이에서는 순서가 바뀔 수 있습니다.

그런데 트리의 BFS에서는 살짝 독특한 점이 있는데, 루트가 아닌 아무 정점이나 잡고 생각을 해보면 인접한 정점들 중에 자신의 부모를 제외하고는 전부 자신의 자식이라 아직 방문하지 않았음이 보장됩니다.
그러니까 예를 들어 6번 정점을 볼 때를 생각해보면, 6번 정점은 4, 7, 8번 정점과 연결되어 있습니다. 4번 정점은 부모이고 또 6번 정점보다 위에 있으니 이미 이전에 방문했을 것이고 7, 8번 정점은 큐에 넣으면 됩니다.
즉 트리에서는 BFS의 과정 속에서 자신의 자식들을 전부 큐에 넣어주기만 하면 됩니다. 이 말은 곧 자신과 이웃한 정점들에 대해 부모만 빼고 나머지는 전부 큐에 넣으면 됨을 의미하고, 그렇기 때문에 vis 배열을 들고갈 필요가 없이 그냥 부모가 누구인지만 저장하고 있으면 됩니다.
부모의 정보는 BFS를 돌리면서 자식 정점을 큐에 집어넣을 때 채워줄 수 있습니다. 다음 장의 코드를 보면서 이해해봅시다.

일단 각 정점의 부모 번호를 저장할 p 배열을 만듭니다. 이 때 루트의 부모는 자연스럽게 0이 됩니다. 12번째 줄에서 nxt가 cur의 부모인지 확인해 만약 부모일 경우엔 건너뜁니다. 부모가 아니면 큐에 넣고 p[nxt] = cur로 만들어줍니다.
vis를 사용할 때와 코드의 흐름이 크게 달라지지는 않습니다. 당연히 시간복잡도도 $O(V+E)$ (인데 $E = V-1$이기에 그냥 $O(V)$가 됩니다.)로 동일합니다.
그러나 이렇게 p 배열을 사용함으로서 "root" 번호의 정점을 루트로 두었을 때 각 정점의 부모 정보를 BFS 한 번으로 알아낼 수 있게 됩니다. 부모 정보가 필요한 문제에서는 이를 활용할 수 있습니다.

p를 계산하는 것에서 추가로 depth를 전부 계산할 수도 있습니다. 자식의 depth는 부모의 depth + 1임을 이용하면 됩니다.

DFS에서도 시작점을 잡으면 그 시작점을 루트로 보낸 상황을 가정하는 것이 편합니다.
위와 같은 트리에서 DFS를 돌리면 1, 2, 5, 3, 4, 6, 7, 8 순으로 방문하게 됩니다. 일단 갈 수 있는 곳 까지 쭉쭉 들어가다가 더 이상 갈 수 없으면 돌아나와 다른 곳으로 간다고 생각하면 편합니다.
BFS와 비슷하게 자신과 연결된 정점들은 1개만 부모이고 나머지는 전부 자식이라는 성질을 이용해 vis 배열을 쓰는 대신 부모 배열과 depth 배열을 채우면서 처리가 가능합니다. 코드를 참고해보세요.

앞의 코드에서 queue만 stack으로 바꾸면 DFS로 처리가 가능합니다.

재귀를 사용하면 코드가 많이 깔끔해집니다.
그러나 전 슬라이드에서도 강조했지만 만약 스택 메모리가 1MB로 제한되어 있을 땐 $V$가 대략 3만 이상일 때 1-2-3-4-5-6-... 형태의 일자 트리 모양에서 스택 메모리 한계를 넘어설 수 있기 때문에 $V$가 클 떄에는 재귀로 DFS를 돌려서는 안됩니다.

단순 순회가 목적이라면 코드가 훨씬 간결해집니다. 굳이 p 배열을 둘 필요 없이 함수 인자로 parent를 넘겨주면 되고, 이렇게 코드를 만들 경우 출력을 제외하면 5줄, 출력을 포함하면 6줄에 DFS를 돌 수 있게 됩니다.
그렇기에 저는 재귀를 이용한 DFS를 굉장히 선호합니다.

그 다음으로 다룰 주제는 이진 트리에서의 순회입니다. 이진 트리는 0x0D강에서 이미 언급했지만 위의 그림과 같이 각 정점의 자식이 최대 2개인 트리를 말합니다.
지금까지 저희가 아는 순회 방식으로는 BFS와 DFS가 있지만 특별히 이진 트리에 대해 따로 이름이 붙은 순회들이 있습니다. 바로 레벨 순회와 전위/중위/후위 순회입니다. 이번 챕터에서는 4가지 순회를 익혀보고자 합니다.
그런데 그 전에 선행되어야 할 것이 있습니다. 바로 이진 트리를 코드에서 표현하는 방법입니다. 물론 이진 트리도 트리의 일종이자 더 나아가 그래프의 특수한 모습이기 때문에 그냥 adj에 넣어서 저장을 할 수는 있습니다. 그러나 이렇게 처리를 해버리면 왼쪽 자식과 오른쪽 자식을 구분할 수가 없게 됩니다.
그렇기에 이 대신에 left와 right를 저장하게끔 코드를 구성해두면 좋습니다. 예쁘게 짜려면 구조체를 만들고 left, right라는 이름의 구조체 변수를 두고 뭐 등등 방법이 있겠지만 이 곳은 실무가 아니라 코딩테스트이기 때문에 거창한 자료구조를 두는 대신 그냥 오른쪽의 코드처럼 lc, rc 배열을 만들면 됩니다. lc는 left child, rc는 right child의 약자입니다. left, right는 이미 namespace std에 존재하는 이름이기 때문에 사용을 피해야 합니다. 사용할 경우 "모호한 기호입니다(ambigious symbol)" 라는 컴파일 에러 메시지를 받게 됩니다. 사실 전 아예 더 줄여서 l 혹은 r로 쓰는 것을 선호하나 그래도 강의자료이니만큼 lc와 rc로 작성을 했습니다.
parents 배열은 사용하지 않더라도 소개할 4가지 순회를 진행할 때에는 문제가 없으나 parents 배열이 필요한 일이 있다면 만들어서 채워두어도 됩니다.
지금은 각 정점의 번호가 그냥 1번부터 차례대로 붙어있기 때문에 별다른 처리가 필요없지만 번호가 1에서 $10^9$ 사이의 수라던가 하는 식으로 된다면 1번부터 차례대로 새롭게 번호를 부여하고 val 배열과 같은 것을 사용해 재배치한 번호와 원래의 번호를 mapping 시키면 됩니다.
0이라는 값은 해당 자리가 비어있음을 의미합니다. 예를 들어 left[4] = 0이니 4의 left child가 없음을 의미합니다.
이 lc와 rc 배열의 값은 코딩테스트 문제에서 입력을 받으며 채워넣을 수 있는데 이 부분은 연습 문제의 풀이를 설명할 때 실제 문제를 예시로 들어 설명하기로 하고 일단 지금은 트리를 배열로 표현할 수 있다는 점만 설명하고 넘어가겠습니다.
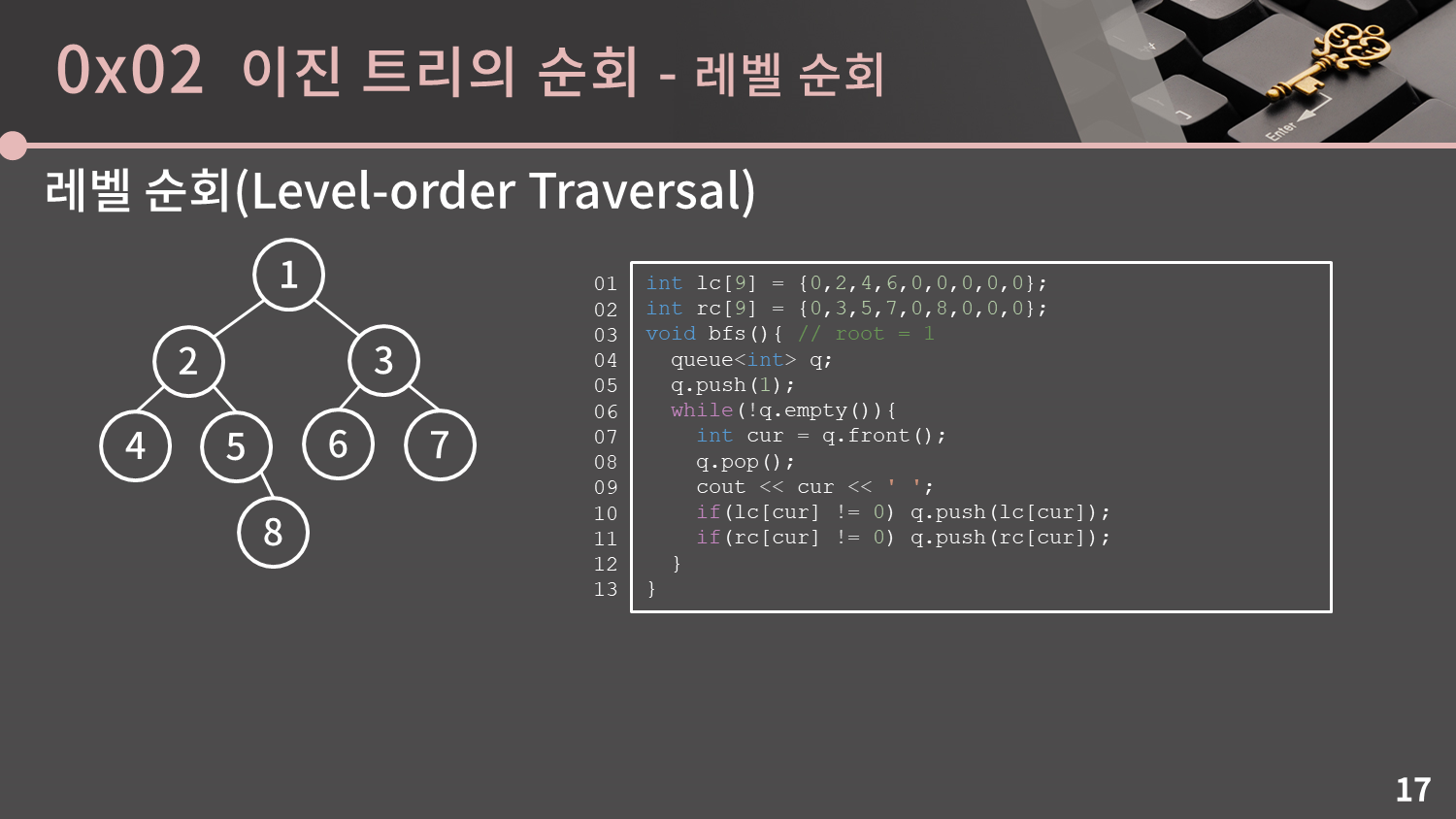
레벨 순회(Level-order Traversal)은 이름 그래도 레벨, 즉 높이 순으로 방문하는 순회입니다. 위의 트리에서는 1, 2, 3, 4, 5, 6, 7, 8 순으로 방문하면 그것이 바로 레벨 순회가 됩니다.
우리는 이미 루트에서 BFS를 돌리면 자연스럽게 레벨 순회가 됨을 알고 있습니다. 그렇기에 레벨 순회는 크게 복잡하게 생각할 필요 없이 그냥 루트를 시작점으로 두고 BFS를 돌림으로서 구현이 가능합니다.
단, 현재는 lc, rc로 이진 트리를 표현하고 있는 상황이기에 이에 맞는 BFS 코드가 필요합니다. 구현은 그다지 어렵지 않은데, 이전 챕터에서 설명했듯 트리에서 BFS를 할 때에는 시작점이 루트라고 가정한 트리 모양에서 현재 보는 정점의 자식을 큐에 넣어주기만 하면 됩니다. 코드를 확인해보세요.
코드의 11, 12번째 줄에서 if(lc[cur] != 0), if(rc[cur] != 0)을 if(lc[cur]), if(rc[cur])로 조금 더 줄여서 작성할 수도 있습니다.

레벨 순회를 제외한 나머지 3개의 순회는 재귀적으로 정의가 됩니다. 조금 헷갈릴 수 있다만 일단 전위 순회의 과정을 이해하고 나면 나머지도 크게 어려움 없이 이해할 수 있을 것입니다.
일단 전위 순회부터 설명을 하겠습니다. 전위 순회는
1. 현재 정점을 방문한다.
2. 왼쪽 서브 트리를 전위 순회한다.
3. 오른쪽 서브 트리를 전위 순회한다.
로 이루어져 있습니다. 왼쪽/오른쪽 서브 트리라는 의미는 나의 왼쪽/오른쪽 자손들이 이루는 트리를 말합니다. 예를 들어 1의 왼쪽 서브 트리는 (2, 4, 5, 8)번 정점으로 이루어진 트리를 뜻하고 2의 오른쪽 서브트리는 (5, 8)번 정점으로 이루어진 트리를 뜻합니다.
재귀는 해도해도 늘 헷갈리는 존재임을 잘 알고 있습니다. 그렇지만 주어진 트리에서 전위 순회를 진행하는 과정을 보여드릴테니 당황하지 말고 같이 차근차근 과정을 따라가봅시다.

루트에서부터 전위 순회를 시작해봅시다. 일단 현재 정점을 방문하라고 하니 1을 방문합니다.

그 다음에는 왼쪽 서브 트리를 전위 순회해야 합니다. 1의 왼쪽 서브트리는 2를 루트로 하는 트리입니다.
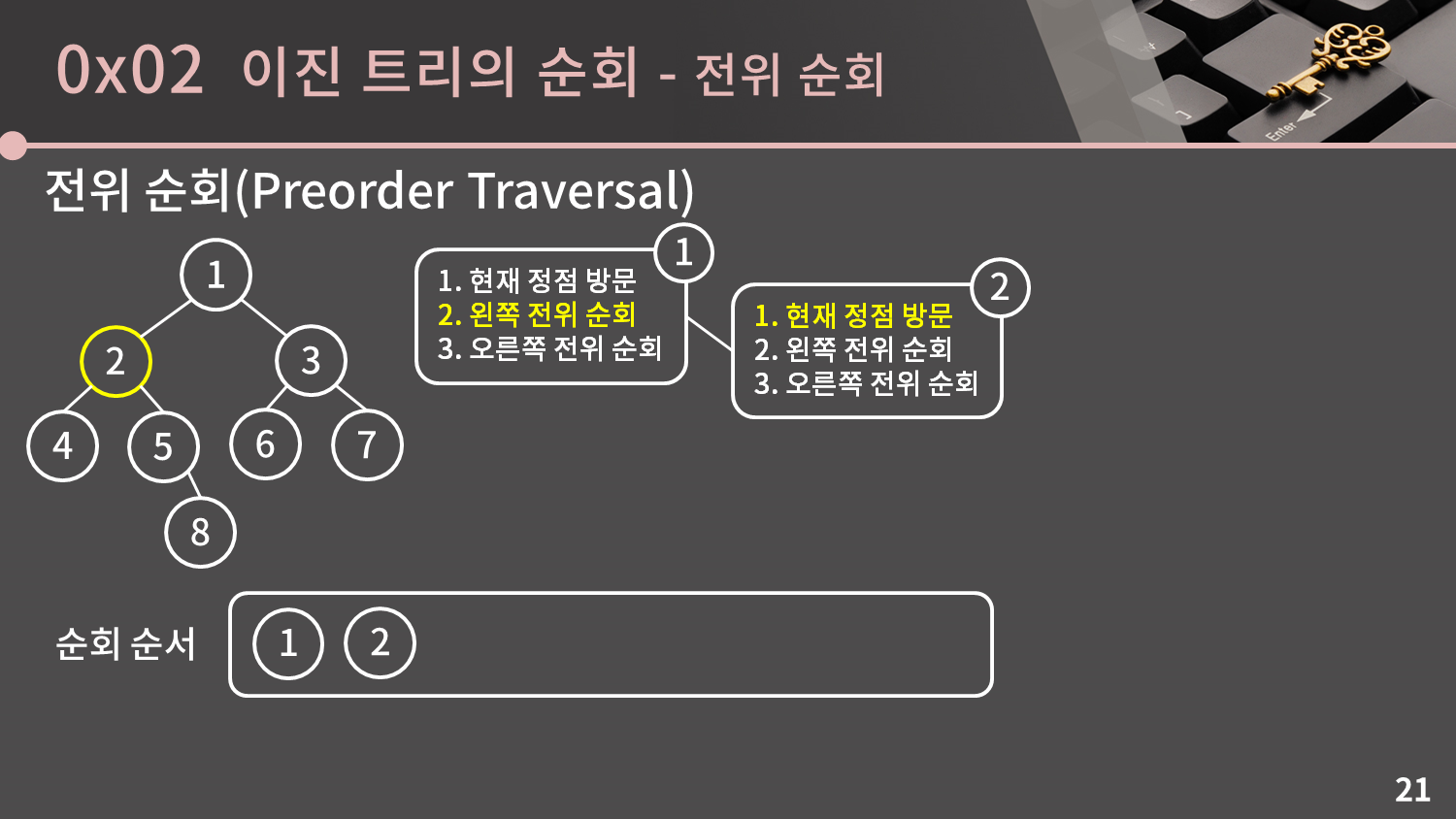
2를 루트로 하는 트리로 넘어와 전위 순회를 다시 시작합시다. 현재 정점인 2를 방문합니다.

그 다음에는 왼쪽 서브 트리를 전위 순회해야 합니다. 2의 왼쪽 서브 트리는 4를 루트로 하는 트리입니다.

4를 루트로 하는 트리로 넘어와 전위 순회를 다시 시작합시다. 현재 정점인 4를 방문합니다.

그 다음으로 4가 루트인 트리에서 왼쪽 서브 트리의 전위 순회를 해야합니다. 그런데 4의 왼쪽 자식이 없기 때문에 4가 루트인 트리는 왼쪽 서브 트리를 가지고 있지 않습니다. 그러므로 아무 것도 하지 않고 넘어갑니다.

그 다음으로 4가 루트인 트리에서 오른쪽 서브 트리의 전위 순회를 해야합니다. 그런데 4의 오른쪽 자식이 없기 때문에 4가 루트인 트리는 오른쪽 서브 트리를 가지고 있지 않습니다. 그러므로 아무 것도 하지 않고 넘어갑니다.
여기서 알 수 있듯 왼쪽과 오른쪽 자식이 모두 존재하지 않는 정점, 즉 리프에서 전위 순회를 시작할 경우 자기 자신만을 방문하고 종료합니다. 앞으로는 리프에 진입한다면 굳이 한 단계 더 들어가지 않고 바로 순회 순서에 추가시킨 후 넘어가겠습니다.

4에서의 순회가 종료되었으니 돌아가 루트가 2인 트리에서 다음 단계인 오른쪽 서브 트리 전위 순회를 할 차례입니다. 4의 오른쪽 서브 트리는 5를 루트로 하는 트리입니다.

5를 루트로 하는 트리로 넘어와 전위 순회를 다시 시작합시다. 현재 정점인 5를 방문합니다.

그 다음으로 5가 루트인 트리에서 왼쪽 서브 트리의 전위 순회를 해야합니다. 그런데 5의 왼쪽 자식이 없기 때문에 5가 루트인 트리는 왼쪽 서브 트리를 가지고 있지 않습니다. 그러므로 아무 것도 하지 않고 넘어갑니다.

그 다음으로 5가 루트인 서브 트리에서 오른쪽 서브 트리의 전위 순회를 해야합니다. 5가 루트인 트리의 오른쪽 서브 트리는 8이 루트인 트리이고, 8은 왼쪽과 오른쪽 자식이 없기에 굳이 들어가지 않고 방문처리를 한 후 넘어가겠습니다.

5에서의 순회가 종료되었으니 돌아갑니다.

2에서의 순회도 종료되었으니 돌아갑니다. 이제 루트가 1인 트리에서 오른쪽 서브 트리의 전위 순회를 하면 됩니다. 지금까지의 예시로도 설명이 충분하다고 생각이 되어 과정을 더 기술하지는 않겠습니다.
오른쪽 서브 트리에서는 3, 6, 7 순으로 방문을 하게 되어 최종적으로 이 트리에서 전위 순회는 1, 2, 4, 5, 8, 3, 6, 7 순으로 이루어집니다.

눈치채셨는지 모르겠는데 전위 순회는 DFS와 방문 순서가 동일합니다. DFS가 일단 자기 자신을 방문한 후 첫번째 자식부터 들어가 거기에서 DFS를 다시 시작하는 구조이기 때문입니다.
그리고 구현은 재귀를 이용해 아주 간단하게 할 수 있습니다. 자기 자신을 출력한 후 왼쪽 자식과 오른쪽 자식 각각에 대해 존재할 경우 전위 순회를 하도록 구현하면 됩니다.

중위 순회는 왼쪽 서브 트리 -> 나 -> 오른쪽 서브 트리 순으로 처리하는 순회 방법입니다. 이미 전위 순회의 예시를 통해 재귀적으로 순회를 도는 것은 익숙하실테니 손으로 직접 순회 순서를 알아내보시는 것을 추천드립니다.
확인해보면 4, 2, 5, 8, 1, 6, 3, 7 순으로 방문이 이루어집니다. 이 순서는 트리의 모양에서 가장 왼쪽에 있는 것 부터 방문하는 순서입니다. 만약 트리가 이진 탐색 트리(=왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 트리)였다면 자연스럽게 크기 순으로 방문하게 됩니다.

마찬가지로 구현은 재귀를 이용해 간단하게 할 수 있습니다. 코드를 확인해보세요.

후위 순회는 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 나 순으로 처리하는 순회 방법입니다. 이것 또한 직접 한번 해보세요.
확인해보면 4, 8, 5, 2, 6, 7, 3, 1 순으로 방문이 이루어집니다. 전위 순회, 중위 순회와 달리 이 순서는 딱히 쉽게 설명할 방법이 없네요.

마찬가지로 구현은 재귀를 이용해 간단하게 할 수 있습니다. 코드를 확인해보세요.

서로 다른 트리라고 하더라도 순회 결과가 일치할 수 있습니다. 위의 두 트리는 중위 순회 결과가 2 1 3으로 동일합니다. 다른 순회들에 대해서도 쉽게 이러한 예시들을 찾을 수 있습니다.
그렇다면 2개의 순회 결과가 주어졌을 때에는 그러한 트리가 유일할까요? 만약 중위 순회(Inorder)와 다른 순회가 주어진다면 유일하지만 중위 순회가 포함되어있지 않다면 유일하지 않습니다. 관련한 얘기는 엄청 중요한 내용이 아닌데 복잡하기까지 해서 하기에 링크를 남길테니 원하시면 들어가서 글을 읽어보세요. 글은 영문입니다.

BOJ 1991번: 트리 순회 문제를 같이 풀어봅시다. 이 문제에서는 주어진 트리의 전위, 중위, 후위 순회 결과를 출력하라고 합니다. 전위, 중위, 후위 순회를 하는 것 자체는 쉬운데 주어진 입력을 lc, rc에 넣는게 조금 어려울 수 있습니다.
한번 시도해보시고 코드를 확인해보세요. 입력을 처리하는 코드는 슬라이드에 나와있는 것과 같이 하면 됩니다. 알파벳을 다루는 것 보다 1, 2, 3, ... 을 다루는 것이 편하므로 이 부분에 대한 처리를 'A'-1 만큼 더하거나 뺌으로서 했습니다. 정답 코드를 확인해보세요.

이번 강의를 통해 여러분은 트리와 이진 트리의 표현법을 익혔고 트리에서 BFS/DFS를 할 수 있게 되었습니다. 그리고 이진 트리에서 4가지 순회를 할 수도 있습니다.
트리의 경우 깊게 들어가면 끝도 없이 어려워지지만 지금까지 배운 범위만으로는 마땅히 낼 문제가 많지는 않습니다. 문제집에 올려둔 2250번 문제를 풀어낼 수 있다면 코딩테스트에서 트리 파트는 크게 걱정하지 않으셔도 될 것입니다. 그러나 트리DP라는 유형의, 재귀적인 처리를 통해 트리에서 Dynamic Programming을 하는 알고리즘의 경우 강의에서는 다루지 않지만 충분히 공부해볼 가치가 있는 유형이니 시간이 남는다면 한 번 학습해보세요.
끝으로 연습 문제를 그룹 내 문제집에 두었으니 풀어보세요.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x13강 - 플로이드 알고리즘_구버전 (9) | 2020.01.28 |
|---|---|
| [실전 알고리즘] 0x12강 - 최소 신장 트리_구버전 (18) | 2020.01.27 |
| [실전 알고리즘] 0x11강 - 위상 정렬_구버전 (13) | 2020.01.17 |
| [실전 알고리즘] 0x0F강 - 그래프_구버전 (21) | 2019.12.22 |
| [실전 알고리즘] 0x0E강 - 문자열(KMP, 라빈 카프)_구버전 (23) | 2019.07.01 |
| [실전 알고리즘] 0x0D강 - 해쉬, 이진 검색 트리, 힙_구버전 (23) | 2019.06.28 |