------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
현재 보고있는 강의는 구버전입니다. 내용에는 문제가 없으나 리뉴얼 중이니 이 게시글을 참고해주세요.
리뉴얼한 버전은 [실전 알고리즘] 0x18강 - 그래프에서 확인할 수 있습니다. 리뉴얼 버전으로 보시는 것을 추천드립니다.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

안녕하세요, 오랜만입니다. 무려 5개월만이네요. 굉장히 늦어진 점 양해 부탁드립니다. 백수(진)이기 때문에 앞으로는 열심히 만들겠습니다.
이전 강좌들에는 ppt에 글씨가 굉장히 많았는데 이번에 형식을 싹 갈아엎었습니다. 완성을 한 후에 이전 강의들도 싹 다 리뉴얼을 할 계획입니다. 리뉴얼 전에 의견 들려주시면 적극 반영하도록 하겠습니다.

수학에서나 일상생활에서 그래프라는 말을 쓸 때는 이런 식으로 데이터를 시각화한 자료를 의미하는데, 자료구조에서 말하는 그래프는 이것과 전혀 상관이 없습니다.

자료구조에서의 그래프는 이 그림과 같이 점과 선으로 이루어진 자료구조를 의미합니다. 이 때 점을 정점(Node or Vertex)으로 부르고 선을 간선(Edge)라고 부릅니다. 또한 각 정점에 연결된 간선의 수를 차수(degree)라고 부릅니다.
그래프는 네비게이션에서 최단경로 찾기,검색엔진에서 랭킹 산정하기 등과 같이 객체 사이의 연결 관계를 설정해야 하는 상황에서 유용하게 활용할 수 있는 자료구조입니다.
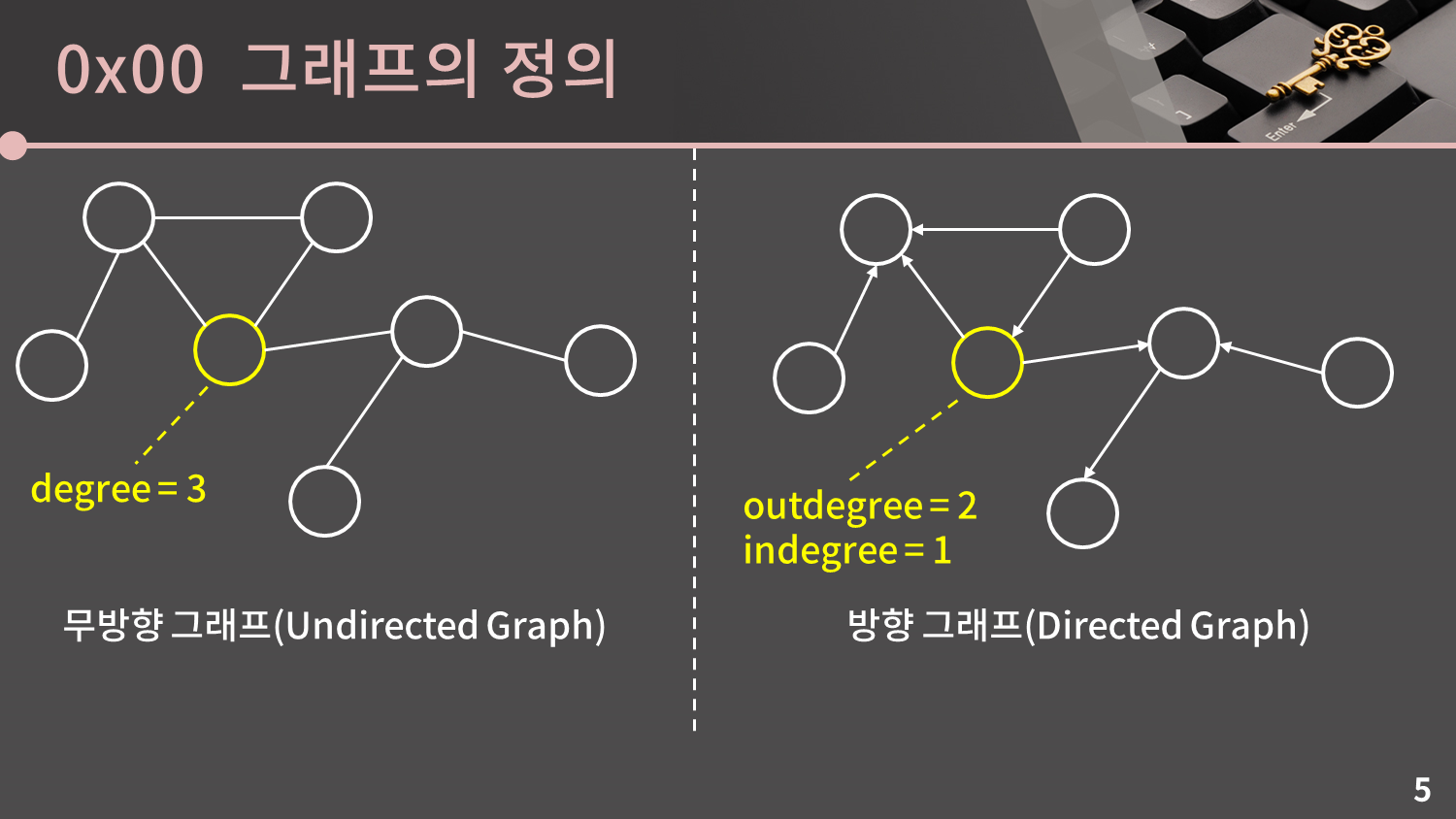
그래프의 간선에 방향성이 없을 경우 무방향 그래프라고 부르고, 방향성이 있을 경우 방향 그래프라고 부릅니다. 간선에 방향성이 있다는 뜻은 간선이 마치 일방통행 도로와 같다고 생각하시면 됩니다.
방향 그래프의 경우 자신에게서 나가는 간선의 수를 outdegree, 들어오는 간선의 수를 indegree라고 부릅니다.

임의의 한 점에서 출발해 자기 자신으로 돌아올 수 있는 경로를 사이클이라고 부릅니다. 그래프 내에 사이클이 존재하면 해당 그래프는 Cyclic Graph라고 부릅니다. 반대로 사이클이 존재하지 않는 그래프는 Acyclic Graph입니다. 오른쪽의 경우 얼핏 보면 왼쪽과 같이 사이클이 있는 것 처럼 보이나 간선의 방향성으로 인해 사이클에 존재하지 않음에 유의하세요.

또한 모든 서로 다른 두 정점 쌍이 간선으로 연결된 그래프를 완전 그래프(Complete Graph)라고 부릅니다. 임의의 두 정점 사이에 경로가 존재하는 그래프는 연결 그래프(Connected Graph)라고 부릅니다.
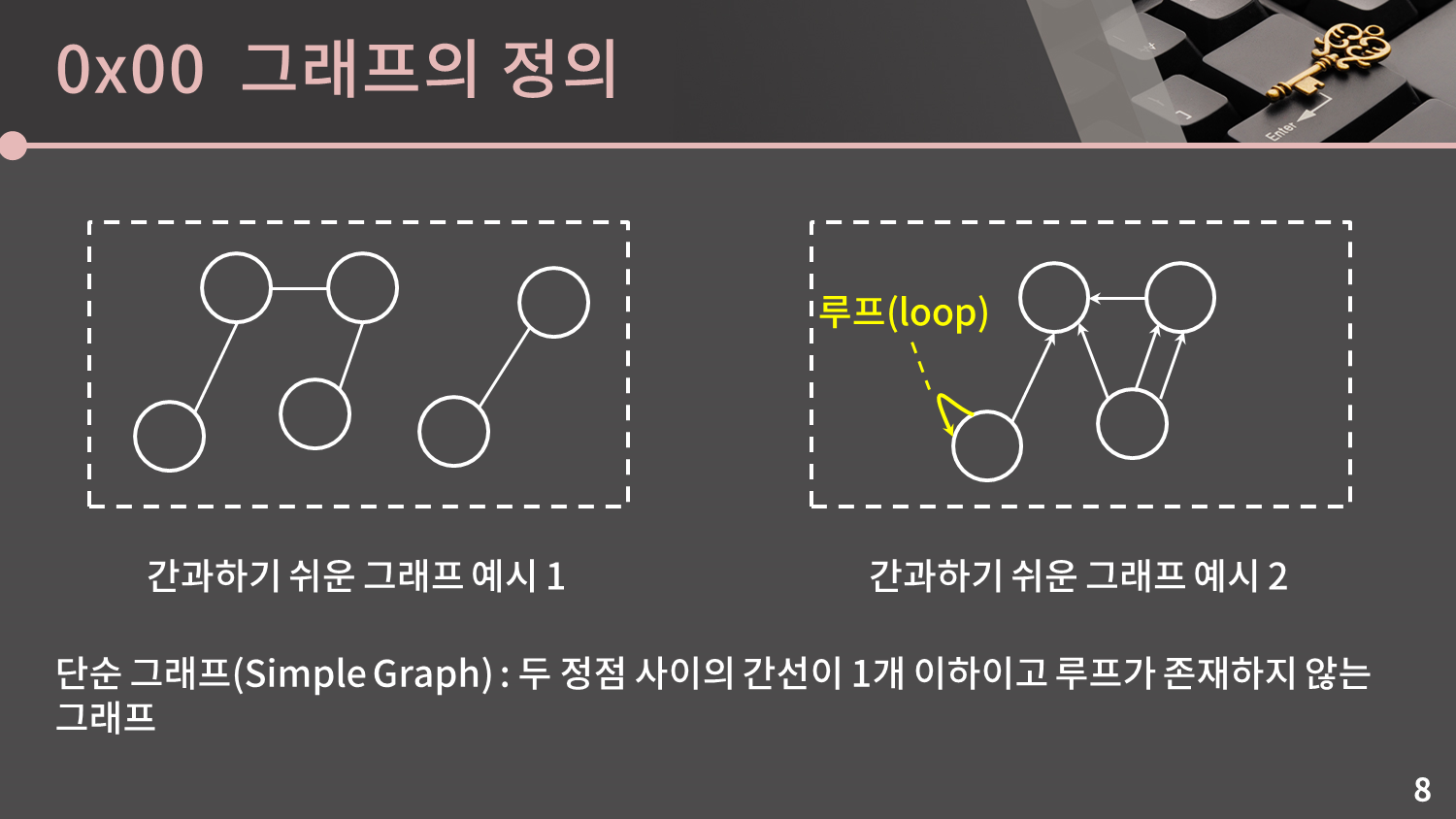
그래프는 꼭 연결되어 있을 필요도 없고, 또 두 정점 사이의 간선이 반드시 1개 이하일 필요도, 또 간선이 반드시 서로 다른 두 정점을 연결해야 할 필요도 없습니다. 참고로 한 정점에서 시작해 같은 정점으로 들어오는 간선을 루프(loop)라고 부릅니다.
보통 문제에서는 필요에 따라 “그래프는 연결되어 있다/그래프는 연결그래프이다“, “두 정점 사이의 간선은 최대 1개 존재한다./같은 간선은 한 번만 주어진다“, “간선의 두 정점은 서로 다르다"와 같이 조건을 엄밀하게 지정하는 경우가 많습니다. 그러나 이러한 말이 없다면 위와 같은 그래프의 형태에 대해서도 정답이 잘 나오도록 해야 합니다.
참고로 두 정점 사이의 간선이 1개 이하이고 루프가 존재하지 않는 그래프를 단순 그래프(Simple Graph)라고 부릅니다.

의외로 그래프라는 개념 자체는 배운 적이 있어서 알고 있지만 이것을 어떻게 코드로 표현해야 할지 모르는 프로그래머가 많습니다. 어떻게 나타내면 될지 같이 배워봅시다.

첫 번째 방법은 인접 행렬(Adjacency Matrix)을 이용하는 방식입니다. 편의상 각 정점에 번호가 붙어있다고 할 때, 연결된 두 정점에는 1을, 연결되지 않은 두 정점에는 0을 주면 그래프를 표현할 수 있습니다. 지금은 Undirected graph이기 때문에 자연스럽게 왼쪽 위와 오른쪽 아래를 연결하는 대각선에 대해 대칭인 형태가 나옵니다.

만약 Directed graph일 경우에는 이런 식으로 표현이 가능합니다. (2, 3)이 1이라는 의미는 2에서 3으로 가는 간선이 있다는 의미입니다.
엄밀히 말해서 1 혹은 0으로만 나타내는 이 표현법은 두 점을 잇는 간선이 여러 개일 경우 문제가 생길 수 있지만 일반적으로는 대부분의 문제에서 주어지는 그래프는 단순 그래프이므로 굳이 고려하지 않겠습니다.
인접 행렬로 그래프를 나타내면 정점이 V개이고 간선이 E개일 때 어떤 두 점이 연결되어 있는지를 $O(1)$에 알 수 있습니다. 가로와 세로가 각각 V인 2차원 배열이 필요하니 $O(V^2)$의 공간을 필요로 합니다. 그리고 어떤 점에 연결되어 있는 모든 정점의 목록을 알아내고 싶을 때에도 갯수와 무관하게 시간복잡도가 $O(V)$입니다.

구현은 굉장히 간단합니다. 일단 정점의 갯수 $V$와 간선의 갯수 $E$가 주어진 후 E줄에 걸쳐 간선이 주어진다고 해봅시다. 이러한 입력 형식은 앞으로 여러분이 풀게 될 대부분의 문제에서 사용하고 있는 입력 형식입니다. 이 때 간선을 입력받으면서 adj_matrix 변수에 1을 적절히 갱신해주기만 하면 됩니다. 간선이 단방향일 경우 adj_matrix[u][v]만 1로 만들고, 양방향일 경우에는 adj_matrix[u][v], adj_matrix[v][u]를 모두 1로 만들면 됩니다.
물론 matrix 크기는 정점의 번호가 1-indexed일 때 $V+1$ by $V+1$ 이상이어야 하고, 현재 코드에서는 10 by 10인데 필요에 따라서 늘리면 됩니다.

두 번째 방법은 인접 리스트(Adjacency List)를 이용하는 방식입니다. 이 방식은 인접 행렬과 비교했을 때 $V$가 크고 $E$가 상대적으로 작은 상황에서 공간을 절약할 수 있는 방식이고, 코딩테스트에서는 인접 행렬보다 훨씬 많이 사용해야하는 방식이기 때문에 잘 익혀두시는게 좋습니다.
개념 자체는 크게 어렵지 않습니다. $V$개의 리스트를 만들어 각 리스트에 연결된 정점을 넣으면 됩니다.
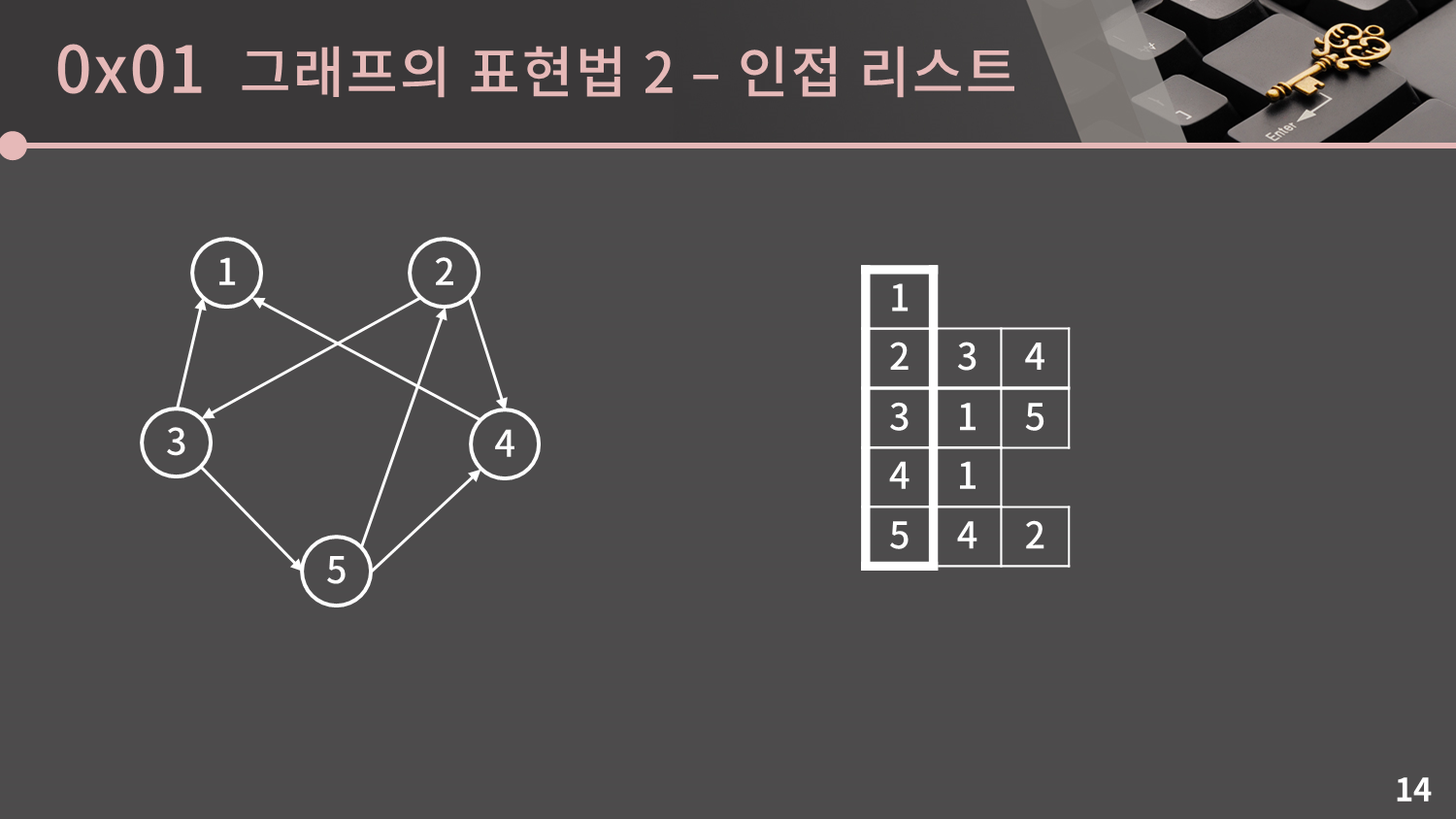
만약 Directed Graph일 경우에는 마찬가지로 양쪽에 다 넣는 것이 아니라 한쪽에만 넣어주면 됩니다.
인접 리스트에서는 $O(V+E)$의 공간이 필요합니다. 일단 리스트가 V개 필요하고, 간선이 1개 있을 때 마다 Directed Graph일 때는 특정 리스트 1개에 원소가 1개 추가되고 Undirected Graph일 때는 특정 리스트 2개에 원소가 1개씩 추가됨을 생각하면 모든 리스트에서 원소의 갯수의 총합은 Directed Graph일 때 E개, Undirected Graph일 때 2E개이기 때문입니다.
그리고 특정 정점과 연결되어 있는 정점들을 순회하고 싶을 때에도 $O(V)$ 대신 딱 갯수만큼만 필요합니다. 예를 들어 3과 연결된 모든 정점을 출력하고 싶을 때 인접 행렬에서는 adj_matrix[3][1], adj_matrix[3][2], ... ,adj_matrix[3][5]를 보아야 했지만 여기서는 3번 리스트에서 원소 2개만 바로 확인하면 됩니다.
공간 복잡도가 $O(V+E)$라는 것은 $V$에 비해 $E$가 작을 때 굉장히 큰 이점을 줍니다. 예를 들어 $V$가 100,000이고 $E$가 200,000인 경우를 생각해봅시다. 이 경우 인접 행렬으로 그래프를 저장하려고 한다면 100,000 by 100,000 배열을 잡아야 하는데 이는 메모리 제한에 걸립니다. 그러나 인접 리스트 방식으로 저장하면 공간복잡도는 $O(V+E)$로 리스트 100,000개가 필요하고 모든 리스트에 저장되는 원소의 총 합이 200,000개 혹은 400,000개 저장되기 때문에 문제 없이 저장이 가능합니다.
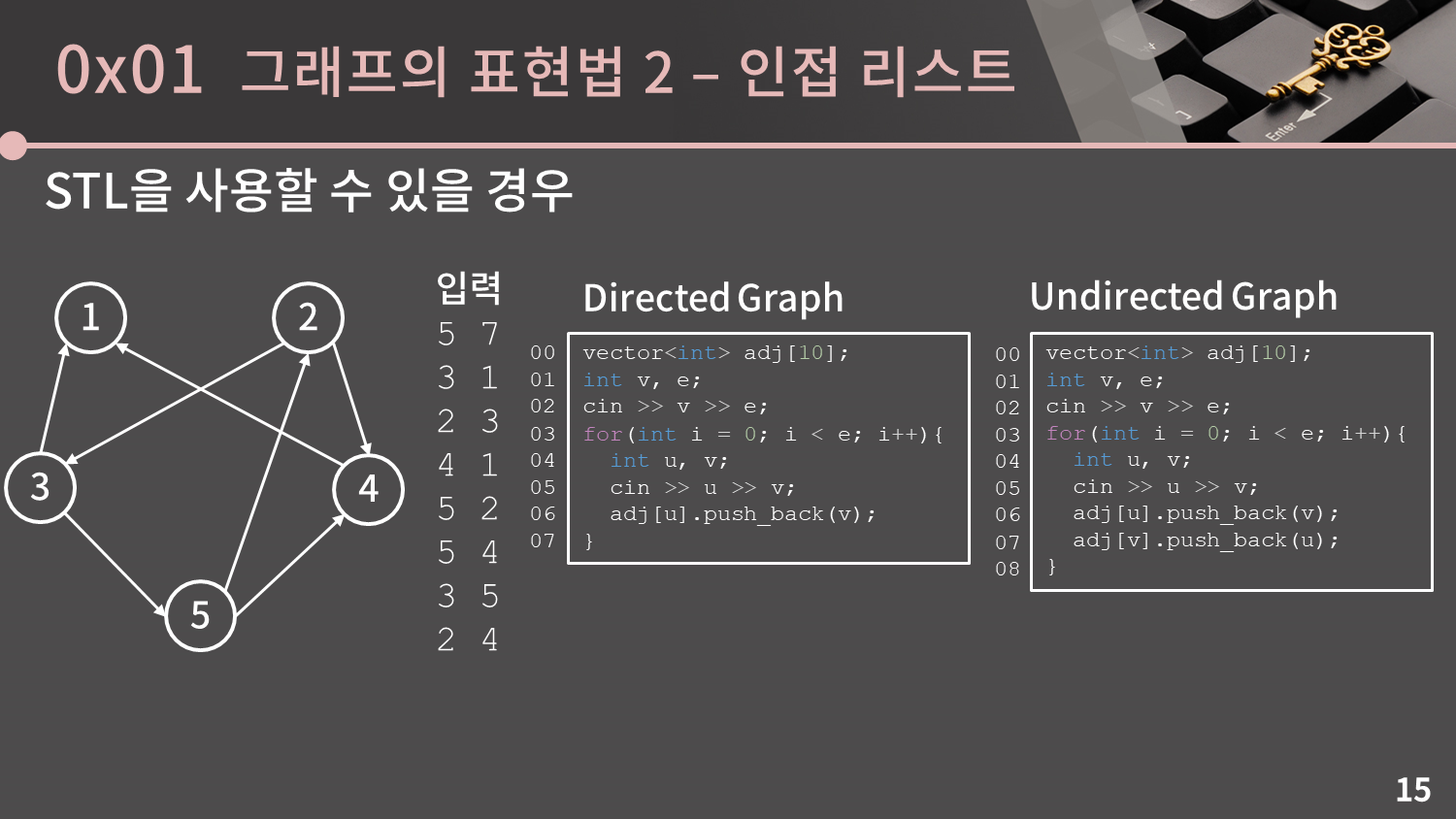
문제는 이것을 어떻게 구현하는가인데, STL을 쓸 수 있는 환경이라고 할 경우 vector를 사용해서 구현하면 어렵지 않습니다. adj[i]는 정점 i와 연결된 정점들의 정보를 가지고 있습니다.

STL을 쓸 수 없는 환경일 때는 조금 까다롭습니다. 예를 들어 $V$가 100,000일 때 그래프가 단순그래프(루프가 존재하지 않고 두 정점을 잇는 간선이 1개 이하인 그래프)라면 각 정점의 degree는 최대 99,999입니다. 즉 한 리스트에 최대 99,999개의 정점이 들어갈 수 있는 것입니다. 하지만 그렇다고 해서 100,000개의 리스트를 전부 크기 99,999개의 배열로 잡아버리면 공간복잡도가 $O(V^2)$가 되어 인접 행렬과 다를 것이 없어집니다.
결국 STL 없이 동적 리스트를 사용할 수 있어야 하는데, 이를 위해 vector나 linked list class를 직접 만들어도 되지만 아무래도 실수할 여지가 많습니다. 대신 위의 코드와 같이 일단 간선의 목록을 입력받으며 차수를 세고, 이후 차수에 맞게 동적 배열을 잡는 식으로 구현을 하면 STL이 없어도 그다지 어렵지 않게 인접 리스트 방식을 구현할 수 있습니다. 이 코드는 방향그래프의 예시입니다.
adj[i]에 동적 할당을 할 때 deg[i]에 1을 더한 크기로 할당을 받는 까닭은 차수가 0일 때 new int[0]; 으로 0칸짜리 배열을 할당받는 것이 다소 꺼림직하게 느껴져서입니다. 1을 더하는 처리가 없어도 상관은 없습니다.

무방향 그래프일 때에는 맨 처음 입력받을 때 deg[edge[i][1]]도 1 증가시켜주고, adj에 추가도 양방향으로 해주는 것에 주의하면 구현은 크게 다르지 않습니다.

이제 여러가지 관점에서 두 표현 방법을 비교해봅시다.

우선 공간 복잡도는 인접 행렬의 경우 $O(V^2)$, 인접 리스트의 경우 $O(V+E)$입니다.
임의의 두 정점이 연결되어 있는지 확인하는 시간 복잡도의 경우, 인접 행렬은 그냥 adj_matrix[u][v]를 확인하면 되니 $O(1)$입니다. 인접 리스트에서는 한 정점에 대해 자신과 연결된 모든 정점을 확인해야 하는데, 둘 중에서 차수가 작은 것을 택해서 확인하는게 이득이므로 $O(min(deg(u), deg(v))$입니다.
한 정점이 연결된 모든 정점을 확인하는 시간 복잡도의 경우, 인접 행렬은 1번부터 $V$번까지에 대해 연결관계를 전부 확인해야 하므로 $O(V)$이지만 인접 리스트에서는 $O(deg(v))$ 입니다.
정리하면 인접 행렬은 두 점의 연결여부를 많이 확인할 때, 혹은 간선의 갯수가 $V^2$에 가까울 때 효율적입니다.
반대로 인접 리스트는 특정 정점에 연결된 모든 정점들을 자주 확인할 때, 혹은 간선의 갯수가 $V^2$보다 훨씬 적을 때 효율적입니다.
예를 들어 $V$가 100,000이고 $E$가 200,000일 경우에는 간선의 갯수 $E$가 $V^2$보다 훨씬 적으므로 인접 리스트를 사용하는 것이 효율적입니다. 반대로 $V$가 100이고 $E$가 7,000일 경우에는 인접 행렬을 사용하는 것이 효율적이긴 합니다. 그러나 일반적인 그래프 문제에서 "정점 u, v가 연결되어있는지를 반복적으로 확인해야 하는 경우"는 거의 없습니다.
또한 다음 챕터에서 배우게 될 BFS, DFS나 앞으로 배울 여러 경로 알고리즘들에서는 전부 특정 정점에 연결된 모든 정점을 확인하는 작업이 반복적으로 등장합니다.
그렇기 때문에 코딩테스트에서는 구현이 간단하다는 점 이외에는 인접 행렬을 사용해서 얻는 이점이 없다고 볼 수 있으며 99% 이상의 경우 인접 리스트로 그래프를 나타낸다고 생각하시면 됩니다.
특이하게 입력 자체가 인접 행렬 느낌으로 주어지거나 $V$가 많이 작아 구현의 편의를 위해 인접 행렬로 푸는 경우가 가끔씩 있지만 기본적으로는 인접 리스트만 다룰 수 있어도 코딩테스트에서 불편함이 없습니다.
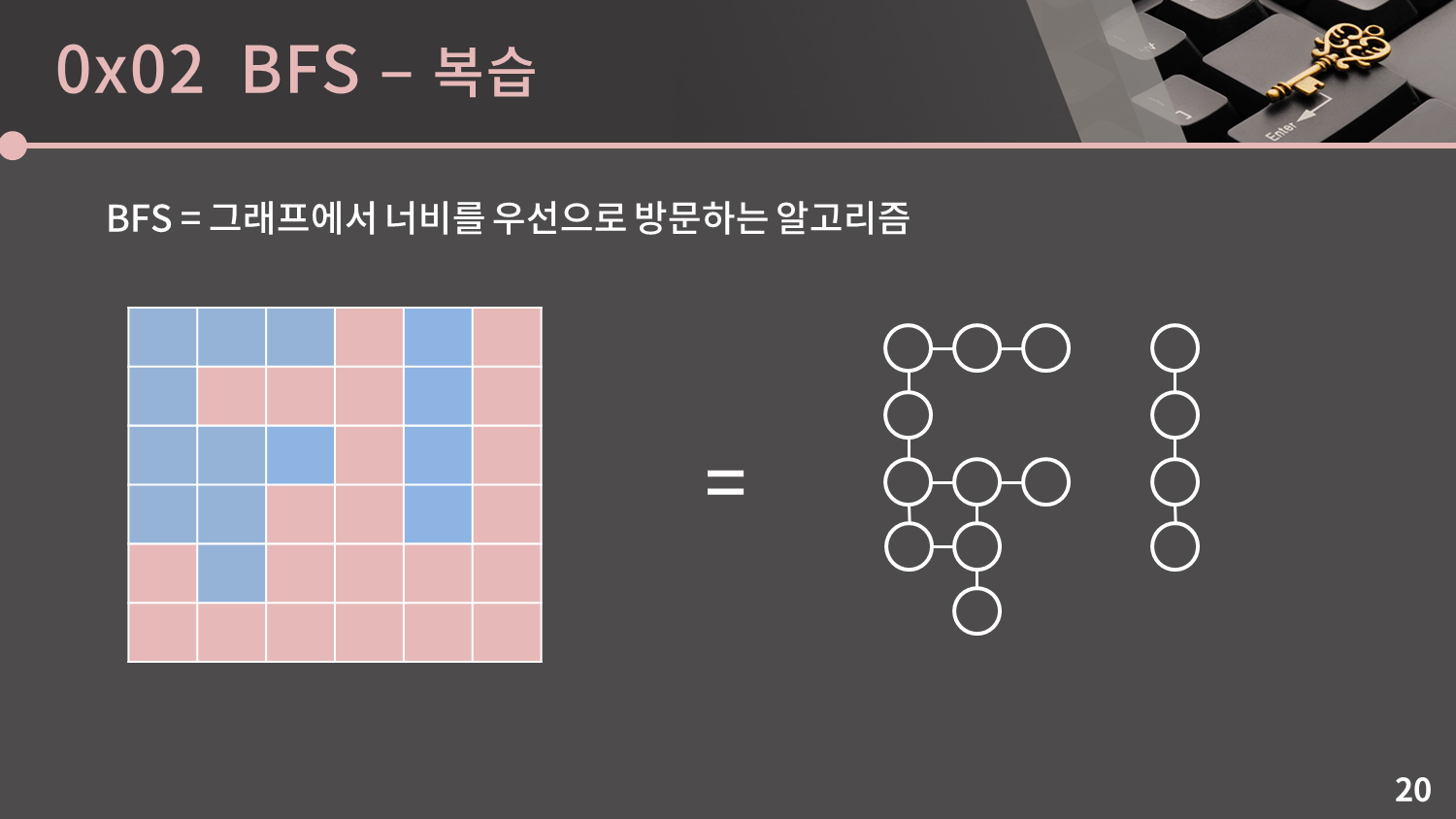
뜬금없이 BFS가 튀어나왔습니다. BFS는 한참 전에 했던 것 같은데.. 왜 그래프에서 BFS가 나오는걸까요?
지금은 기억이 잘 안나시겠지만 0x05강에서 BFS를 처음 소개할 때 이렇게 표현했습니다. “BFS는 다차원 배열에서 각 칸을 방문할 때 너비를 우선으로 방문하는 알고리즘입니다. 원래 BFS와 DFS는 그래프 자료구조에서 모든 정점을 순회하기 위한 알고리즘으로, 다차원 배열이 그래프 자료구조의 특수한 형태이기 때문에 다차원 배열에서도 BFS, DFS를 사용할 수 있는 것입니다.”
즉, 지금까지는 다차원 배열에서 BFS와 DFS를 사용했지만 사실 BFS와 DFS는 그래프 자료구조에서 모든 정점을 순회할 때 쓰이는 알고리즘입니다. 예를 들어 왼쪽의 2차원 맵을 사실 오른쪽의 그래프와 같이 생각해도 상관이 없습니다. 파랑이 갈 수 있는 칸이고 빨강이 갈 수 없는 칸입니다.
이미 2차원 배열에서의 BFS에는 충분히 익숙하실테니 그래프에서의 BFS도 쉽게 이해하실 수 있습니다. 같이 한 번 과정을 따라가보겠습니다.

우선 방법을 글로 나타내면 이렇습니다. 2차원 배열에서 BFS를 할 때와 크게 다르지 않습니다.
2차원 배열에서는 상하좌우로 인접한 칸에 대해 살펴봤다면 그래프에서는 연결된 모든 정점을 살펴본다는 점만 차이가 있습니다. 만약 그래프가 Directed Graph일 때에는 자신으로부터 나가는 간선으로 연결된 점들만 살펴보면 됩니다.
인접 행렬일 경우에는 3번 과정이 $O(V)$가 필요하고 3번 과정을 $V$번에 걸쳐 진행하므로 $O(V^2)$임을 받아들일 수 있을 것입니다.
그러나 인접 리스트에서 시간복잡도가 $O(V+E)$인게 조금 헷갈릴 수 있는데, 모든 정점들에 대해 그 정점과 연결된 모든 정점을 살펴보는 과정의 총 합이 Directed Graph에서 $E$, Undirected Graph에서 $2E$가 필요해서 그런 것입니다. 잘 이해가 안간다면 다음 슬라이드의 그림을 참고해주세요.

“모든 정점들에 대해 그 정점과 연결된 모든 정점을 살펴보는 과정의 총 합이 Undirected Graph에서 $2E$이다” 라는 말을 그림으로 이해시켜드리겠습니다. 현재 간선은 8개입니다.
7개의 각 그래프는 1번부터 7번까지의 정점이 자신과 연결된 정점을 탐색하는 상황을 나타낸 것입니다.
그림을 살펴보면 각 간선은 2번씩 등장합니다. 이는 논리적으로 생각해도 당연한게 u와 v를 연결하는 간선은 u와 연결된 모든 정점을 살펴볼 때, 그리고 v와 연결된 간선을 살펴볼 때 한 번씩 등장하겠죠. 그리고 만약 directed graph였다면 u에서 v로 가는 간선은 u와 연결된 모든 정점을 살펴볼 때에만 등장하게 됩니다.
그러므로 앞에서 설명한 2번 “모든 정점들에 대해 그 정점과 연결된 모든 정점을 살펴보는 과정”은 $2E$ 혹은 $E$번의 탐색을 필요로 하고, 이로 인해 시간복잡도가 $O(V+E)$ 이 됩니다.
다시 한 번 강조하지만 시간복잡도에 $E$가 포함된다는 것을 유념하셔야 합니다.
예를 들어 V가 2,000인 완전그래프(=모든 서로 다른 두 정점 쌍이 간선으로 연결된 그래프)에서 간선은 대략 2,000,000개인데 여기서 BFS를 1000번 돌리는 풀이를 생각한 경우 이것의 시간복잡도는 $O(1000V)$가 아니라 $O(1000(V+E))$이고 시간초과가 발생하게 됩니다.
그러면 BFS를 같이 한번 해봅시다.

이제 직접 BFS를 해보겠습니다. 시작 정점은 어느 것이어도 상관이 없지만 임의로 1번부터 시작하겠습니다.
일단 1번 정점을 큐에 넣고 방문했다는 표시를 남깁니다.
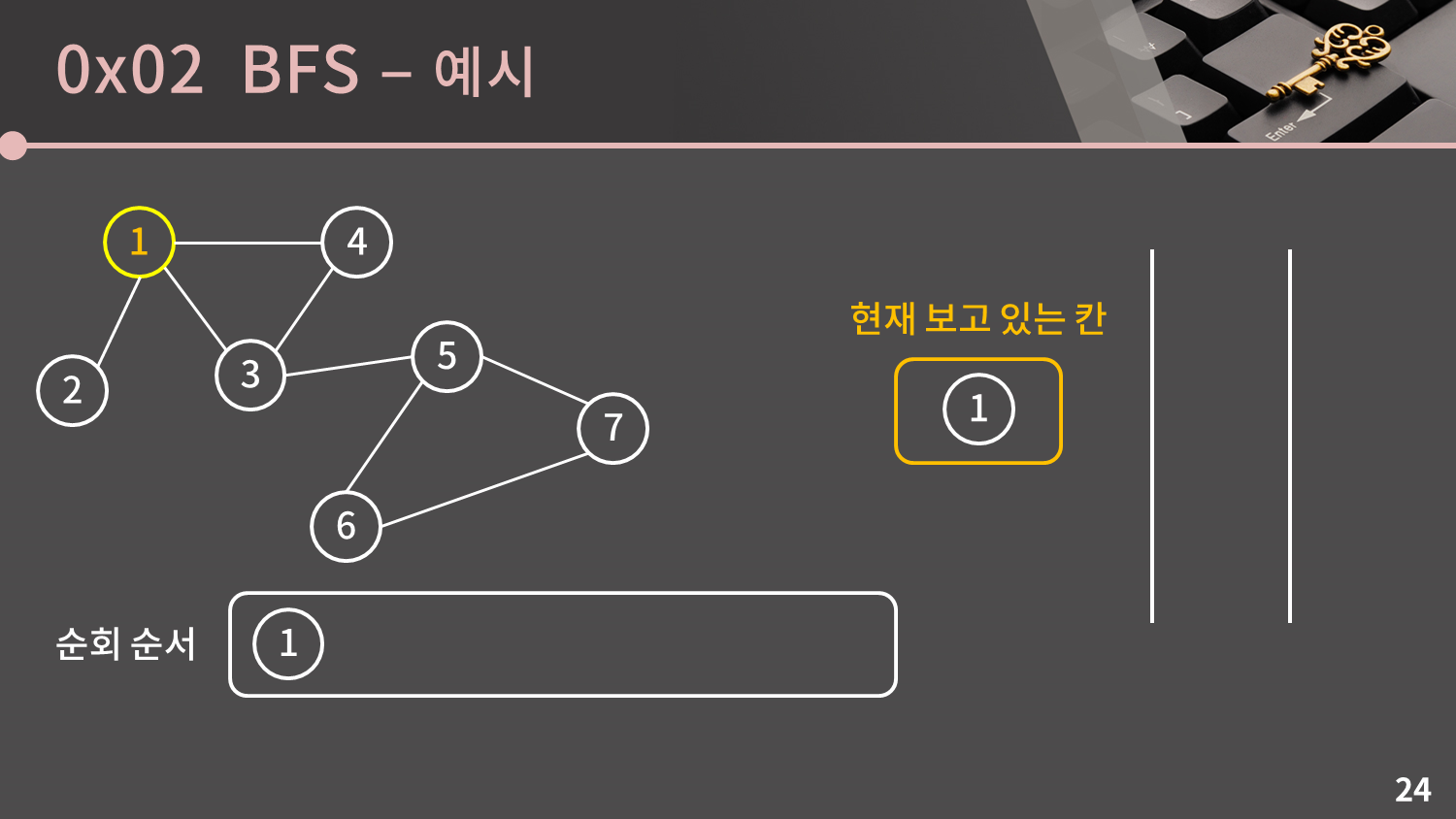
큐가 비어있지 않으므로 큐의 front인 1번 정점을 꺼냅니다.

1번 정점과 이웃한 2, 3, 4번 정점은 모두 아직 방문하지 않은 정점이므로 방문했다는 표시를 남기고 큐에 넣습니다.
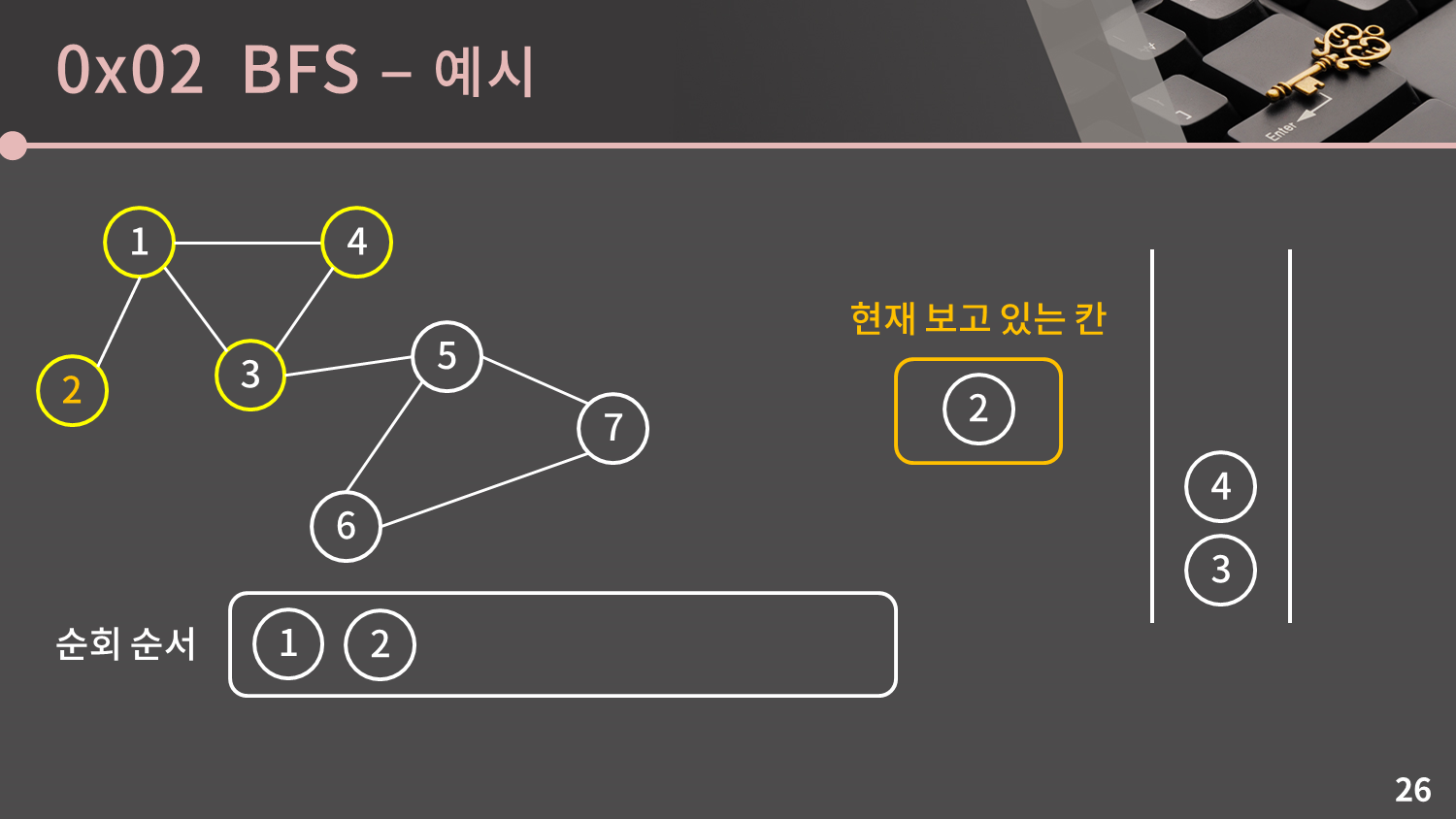
큐가 비어있지 않으므로 큐의 front인 2번 정점을 꺼냅니다. 2번 정점과 이웃한 1번 정점은 이미 방문한 정점이므로 넘어갑니다.
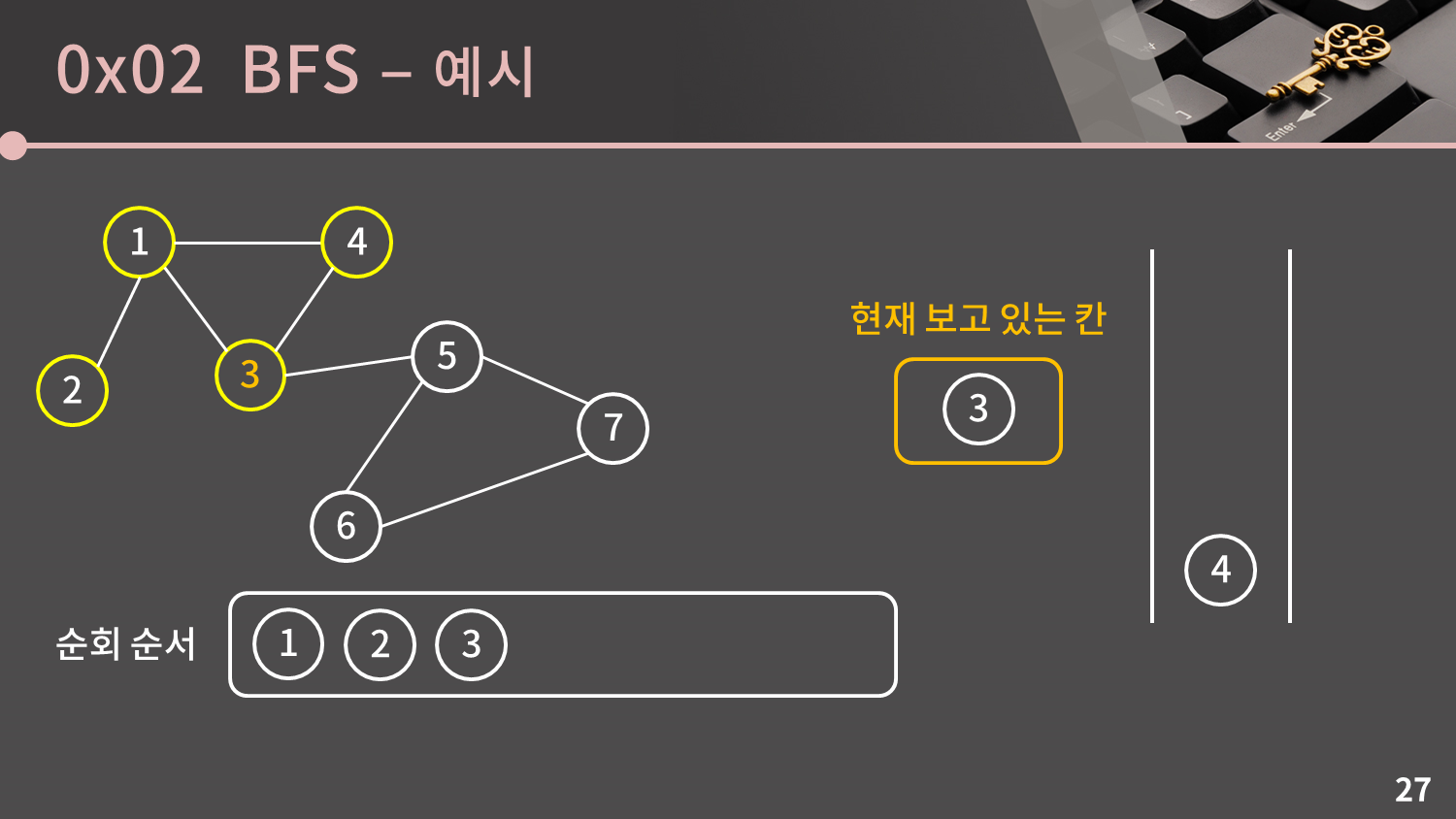
큐가 비어있지 않으므로 큐의 front인 3번 정점을 꺼냅니다.

3번 정점과 이웃한 정점은 1, 4, 5번 정점입니다. 이 중에서 5번 정점만 유일하게 방문하지 않은 정점이므로 방문했다는 표시를 남기고 큐에 넣습니다.

큐가 비어있지 않으므로 큐의 front인 4번 정점을 꺼냅니다. 4번 정점과 이웃한 1, 3번 정점은 이미 방문한 정점이므로 넘어갑니다.

큐가 비어있지 않으므로 큐의 front인 5번 정점을 꺼냅니다.

5번 정점과 이웃한 3, 6, 7번 정점 중에서 3번 정점은 이미 방문한 정점입니다. 6, 7번 정점은 아직 방문하지 않은 정점이므로 방문했다는 표시를 남기고 큐에 넣습니다.
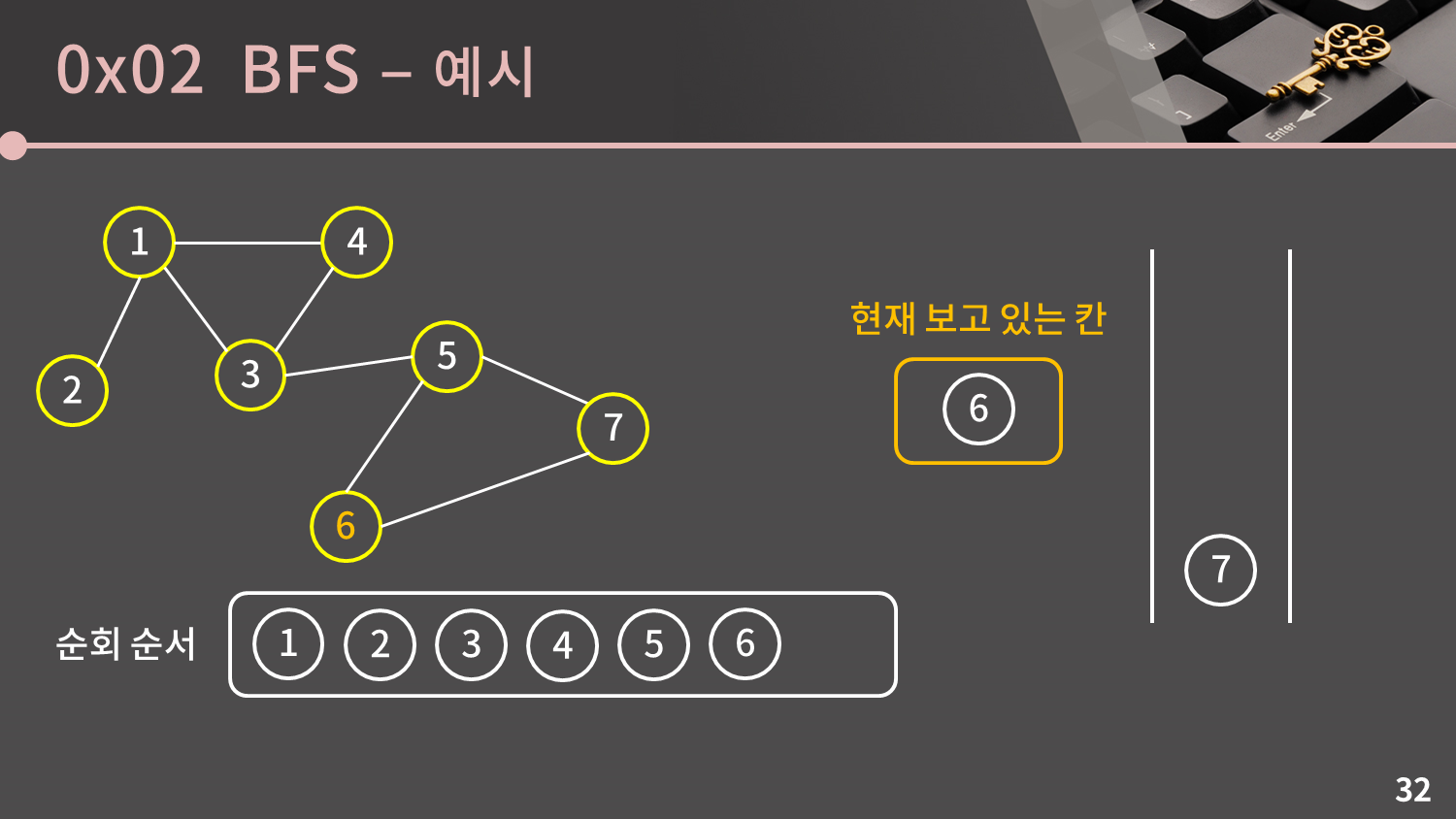
큐가 비어있지 않으므로 큐의 front인 6번 정점을 꺼냅니다. 6번 정점과 이웃한 5, 7번 정점은 이미 방문한 정점이므로 넘어갑니다.
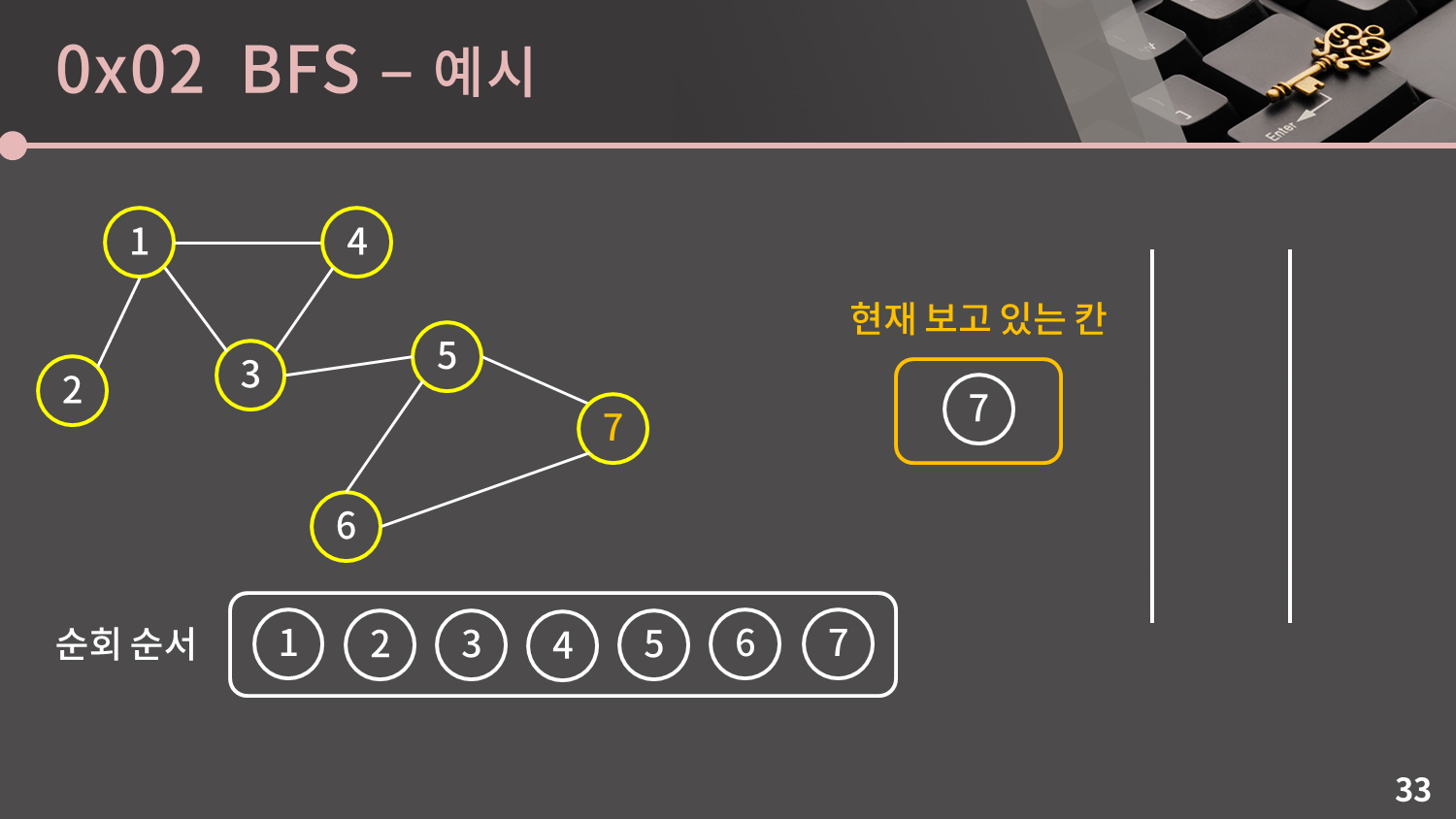
큐가 비어있지 않으므로 큐의 front인 7번 정점을 꺼냅니다. 7번 정점과 이웃한 5, 6번 정점은 이미 방문한 정점이므로 넘어갑니다.
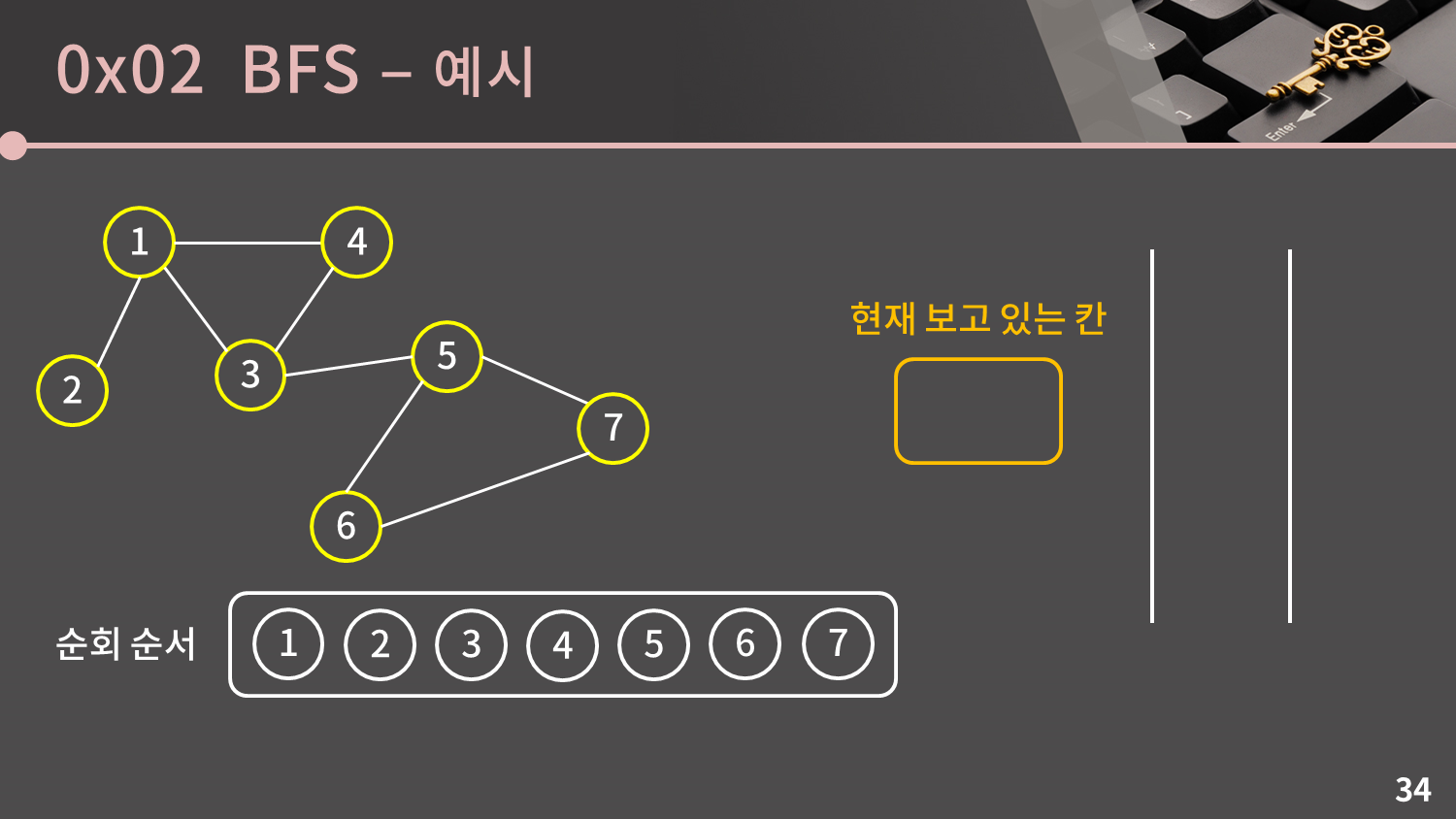
큐가 비었으므로 과정이 종료됩니다.

그래프의 BFS에서도 2차원 배열의 BFS와 동일하게 시작점에서 다른 모든 점으로의 최단 경로를 찾을 때 이용할 수 있습니다.
BFS의 과정 속에서 현재 보는 정점으로부터 추가되는 인접한 정점은 시작점으로부터 1만큼 더 떨어져 있습니다.
즉, 모든 간선의 길이가 동일한 상황에서 두 지점 사이의 거리를 찾는 문제는 BFS로 해결이 가능합니다. 그러나 만약 모든 간선의 길이가 다르다면 이 문제는 Floyd, Dijkstra, Bellman Ford와 같은 다른 알고리즘을 사용해야되고 이러한 알고리즘은 몇 강 후에 배우게 될 것입니다.

이 예시 코드는 순회만 하는 코드입니다. 인접 리스트 방식으로 그래프가 저장되어 있고 정점은 1번부터 순차적으로 매겨져있다고 가정합니다.
이미 2차원 배열에서 BFS를 많이 해보았기 때문에 코드의 흐름이 크게 낯설지 않을 것입니다.
만약 C++11이 지원되는 환경이라면 for문에서 i를 0부터 adj[cur].size까지 증가시키는 대신 for(auto nxt : adj[cur]) 로 타이핑을 덜 낭비하고 구현할 수 있습니다.
만약 STL이 지원되지 않는 환경이라면 큐를 별도로 구현하고 i를 adj[cur].size 대신 deg[cur]까지 증가시키면 될 것입니다.
큐에 넣은 직후에 vis의 값을 true로 갱신해줘야 함에 유의해야 합니다.
인접 행렬로 BFS를 구현하면 시간복잡도가 $O(V^2)$으로 더 비효율적이라 비추천하지만, 굳이 필요하다면 for문 부분을 for(int nxt = 1; nxt <= V; nxt++)으로 변경하고 adj_matrix[cur][nxt]가 1일 때만 아래의 과정을 진행하도록 코드를 수정하면 됩니다.

이 예시 코드는 1번 정점과의 거리를 구하는 코드입니다. 두 정점 사이의 거리는 거쳐야 하는 간선의 최소 갯수로 정의하면 됩니다.
dist를 먼저 -1로 초기화시키는 것을 빼먹으면 안됩니다.
0으로 초기화시키고 자기 자신과의 거리를 1로 두어도(즉 dist[1] = 1로 두어도) 상관은 없습니다.
맨 처음 for문으로 dist를 초기화시키는 과정을 fill(dist+1, dist+10, -1); 로 나타내면 타이핑을 절약할 수 있습니다.
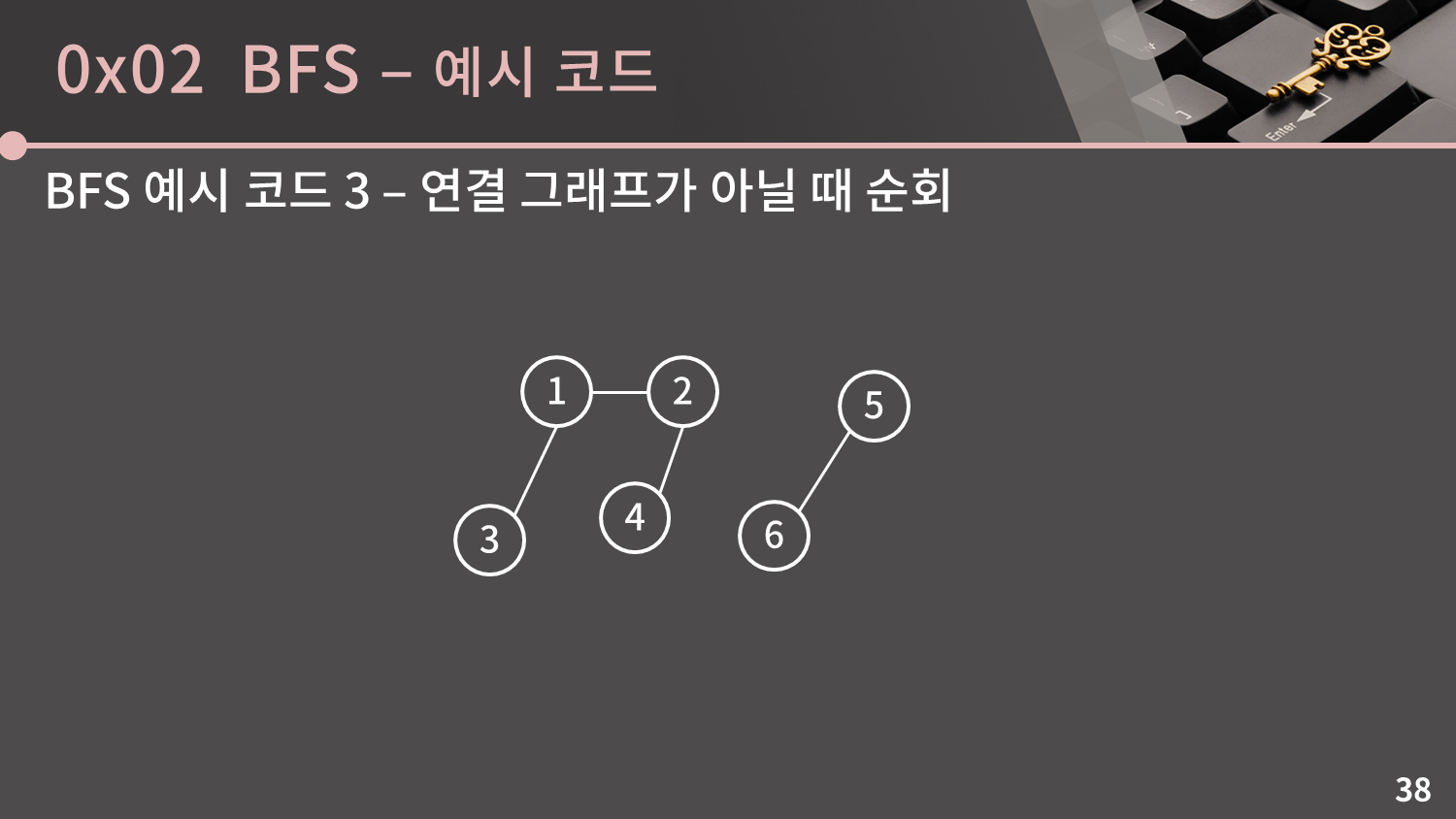
예시 코드 1은 연결 그래프가 아닐 경우 모든 정점을 방문할 수 없습니다. 예를 들어 위와 같은 그래프라면 예시 코드 1이 5번과 6번 정점을 순회하지 못하게 될 것입니다. 이를 해결하기 위해 1번만을 시작 정점으로 잡는 대신 모든 아직 방문하지 않는 정점을 시작 정점으로 잡게끔 코드를 변형하면 됩니다. 코드 예시를 확인해보세요.


그 다음은 DFS입니다. 큐로 처리하던 것을 스택으로 한다는 점만 다르고 전반적인 흐름은 BFS와 동일하기 때문에 굳이 과정에 대한 설명을 다시 하지는 않겠습니다. 예시를 같이 봅시다.

DFS도 같이 해봅시다. 시작 정점은 어느 것이어도 상관이 없지만 임의로 1번부터 시작하겠습니다.
일단 1번 정점을 스택에 넣고 방문했다는 표시를 남깁니다.

스택가 비어있지 않으므로 스택의 top인 1번 정점을 꺼냅니다.
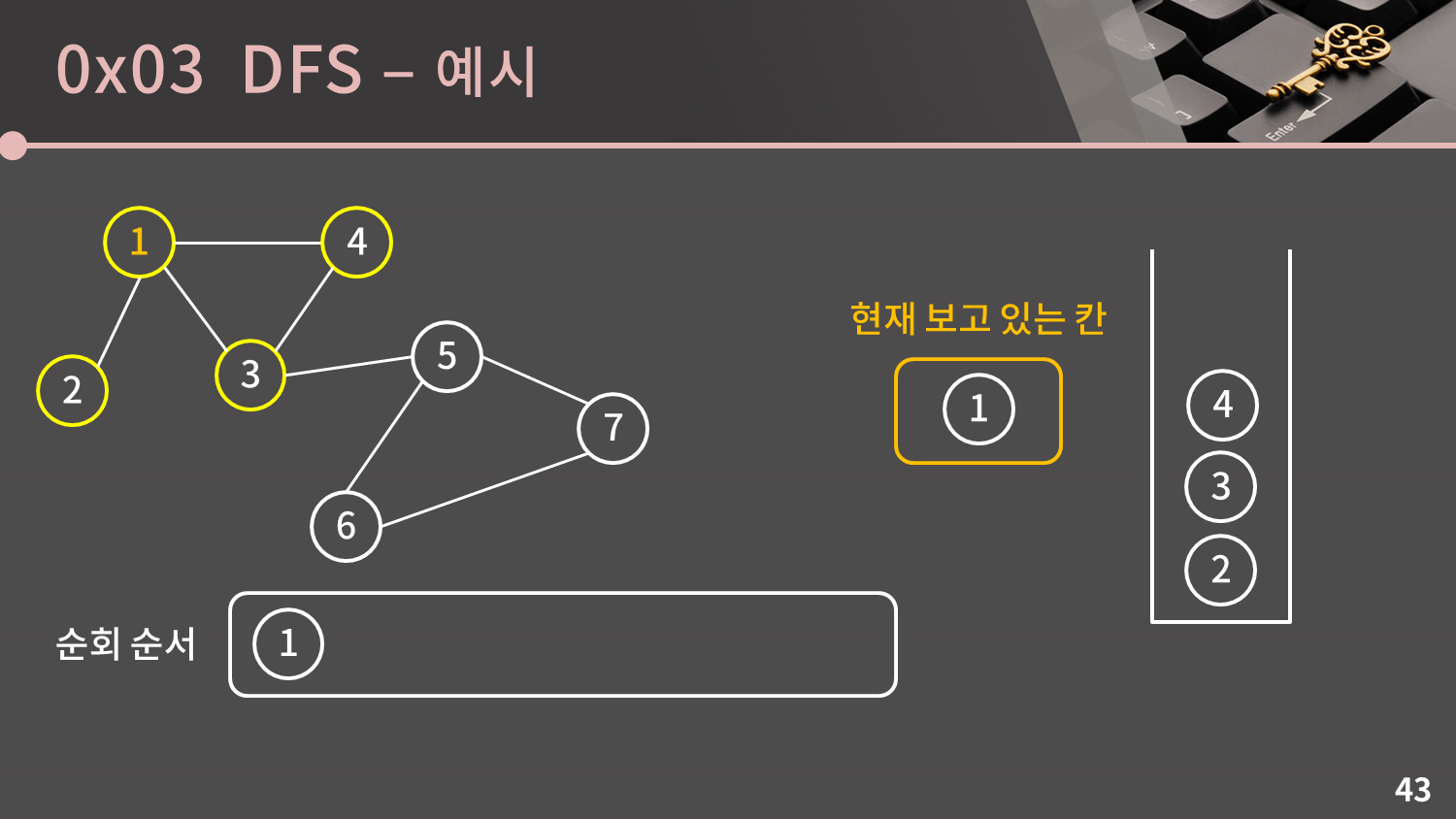
1번 정점과 이웃한 2, 3, 4번 정점은 모두 아직 방문하지 않은 정점이므로 방문했다는 표시를 남기고 스택에 넣습니다.

스택이 비어있지 않으므로 스택의 top인 4번 정점을 꺼냅니다. 4번 정점과 이웃한 1, 3번 정점은 이미 방문한 정점이므로 넘어갑니다.
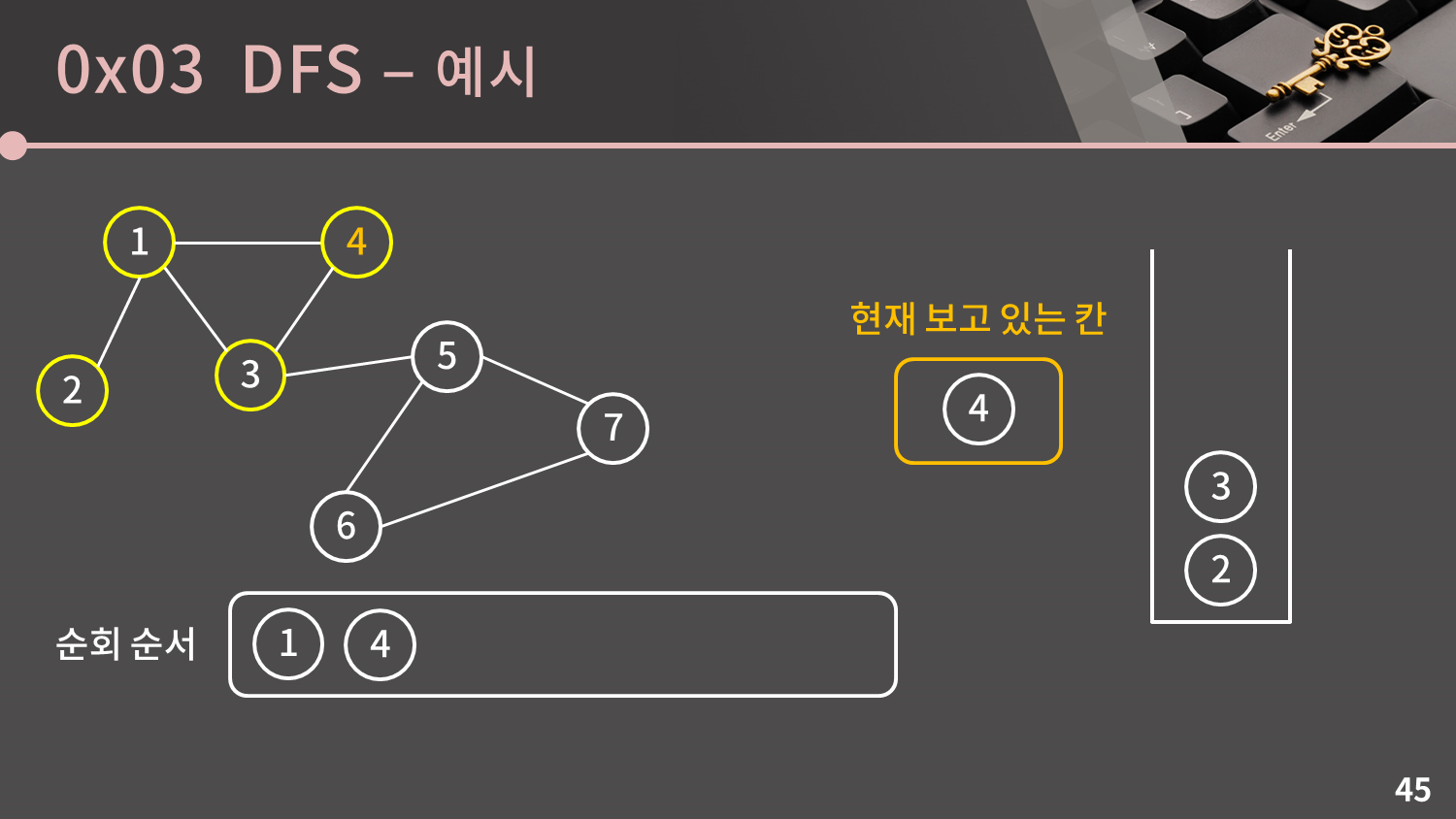
스택이 비어있지 않으므로 스택의 top인 4번 정점을 꺼냅니다. 4번 정점과 이웃한 1, 3번 정점은 이미 방문한 정점이므로 넘어갑니다.

스택이 비어있지 않으므로 스택의 top인 3번 정점을 꺼냅니다.
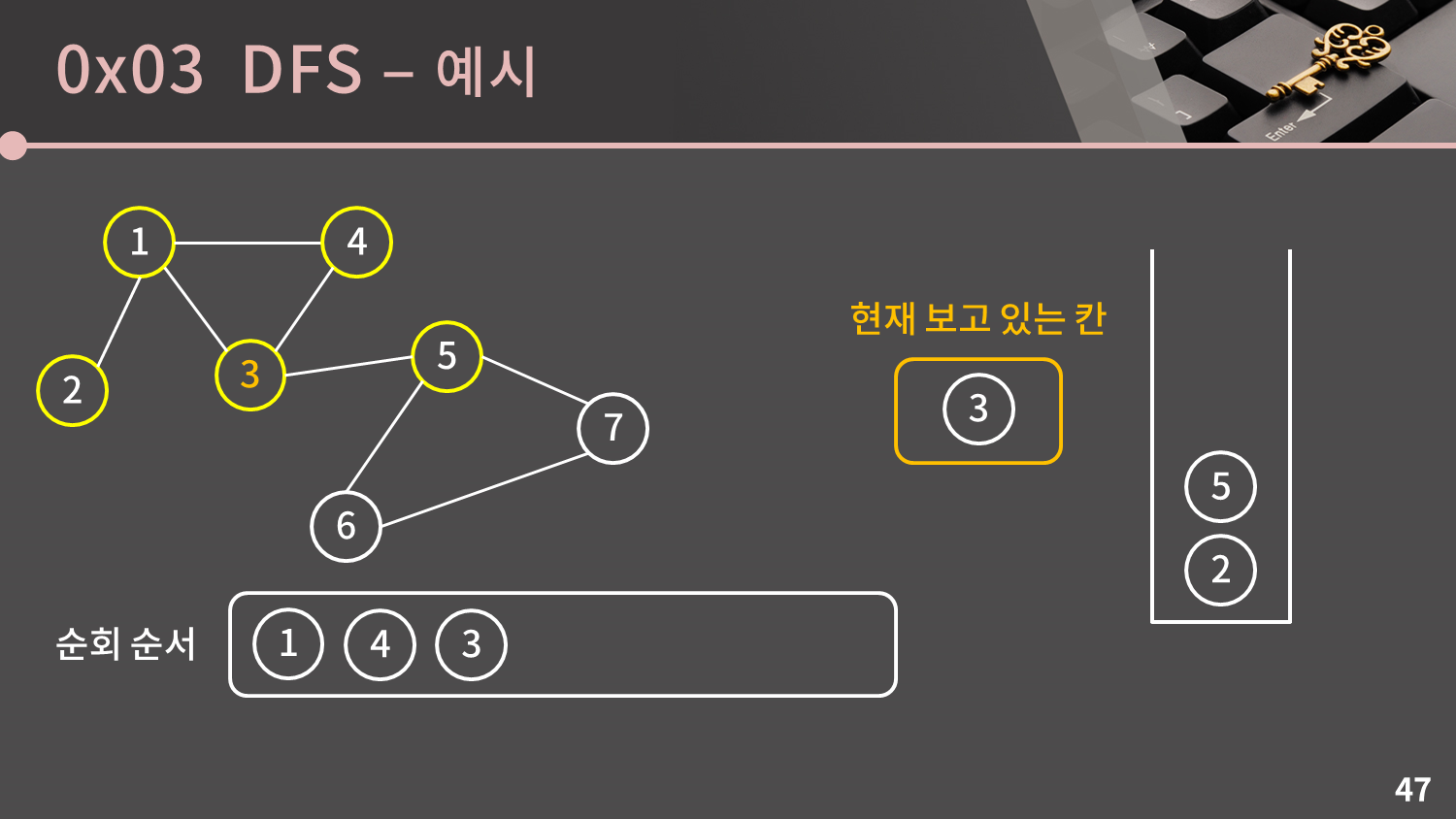
3번 정점과 이웃한 정점은 1, 4, 5번 정점입니다. 이 중에서 5번 정점만 유일하게 방문하지 않은 정점이므로 방문했다는 표시를 남기고 스택에 넣습니다.
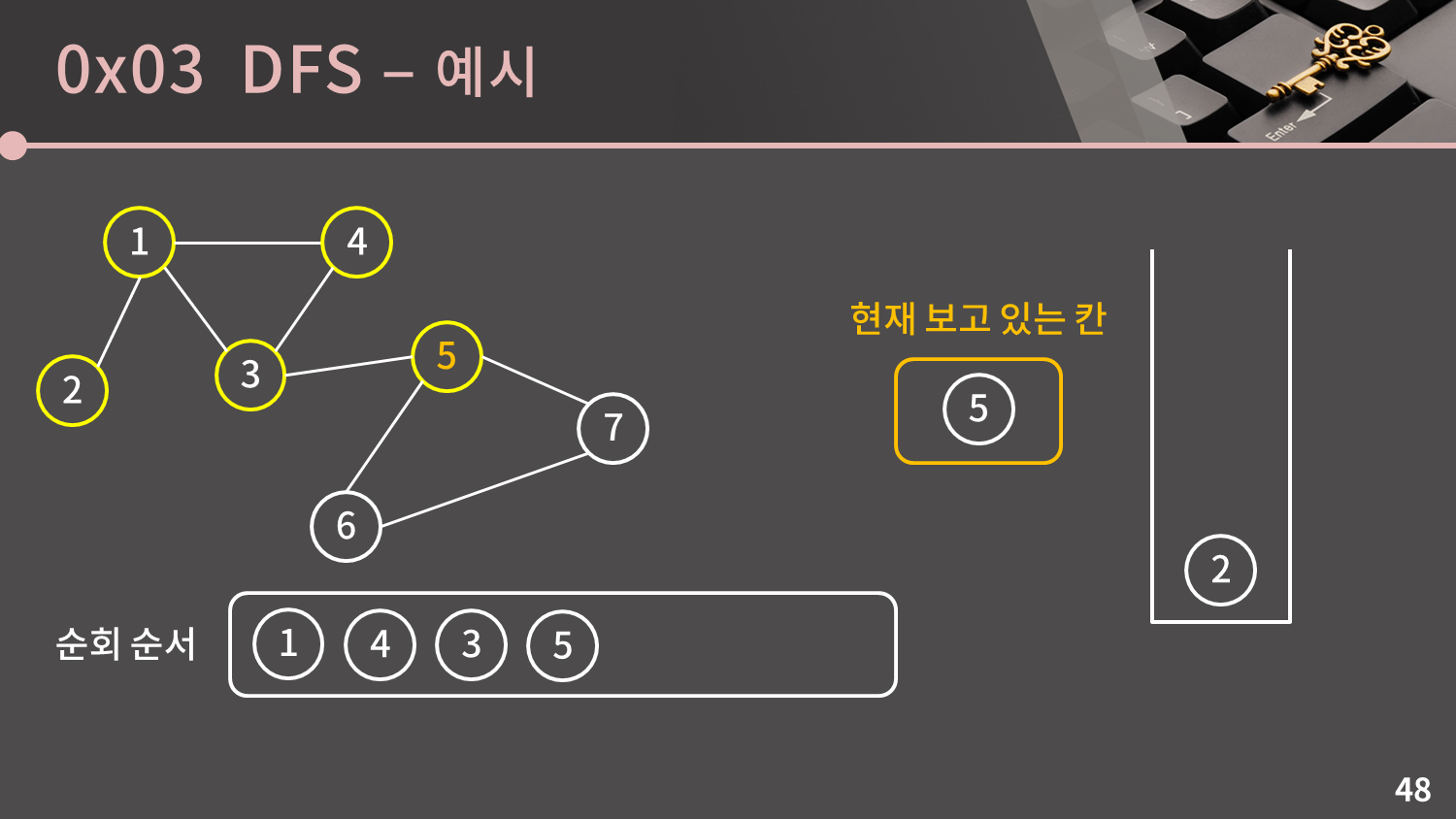
스택이 비어있지 않으므로 스택의 top인 5번 정점을 꺼냅니다.
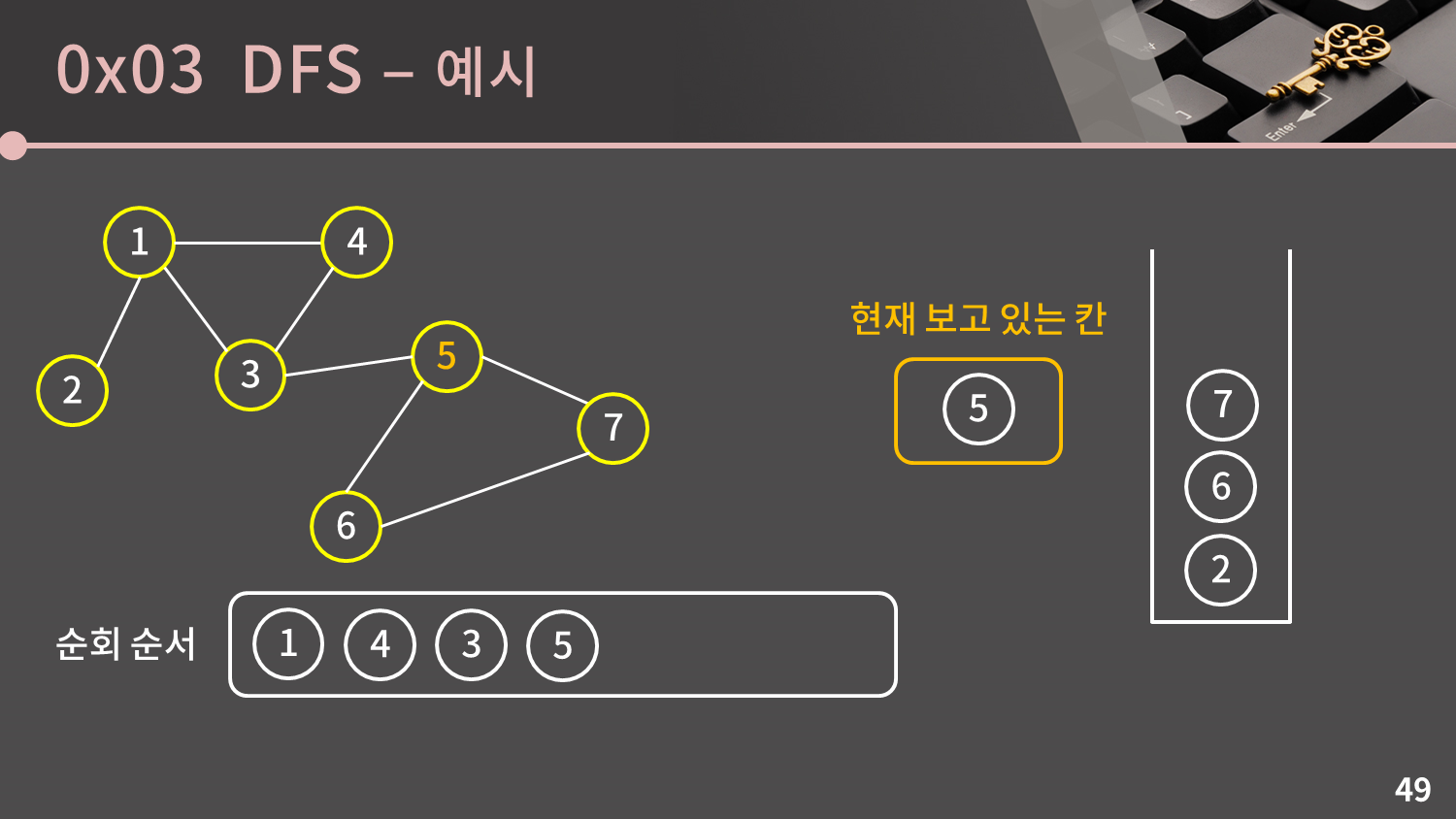
5번 정점과 이웃한 3, 6, 7번 정점 중에서 3번 정점은 이미 방문한 정점입니다. 6, 7번 정점은 아직 방문하지 않은 정점이므로 방문했다는 표시를 남기고 스택에 넣습니다.

스택이 비어있지 않으므로 스택의 top인 7번 정점을 꺼냅니다. 7번 정점과 이웃한 4, 6번 정점은 이미 방문한 정점이므로 넘어갑니다.
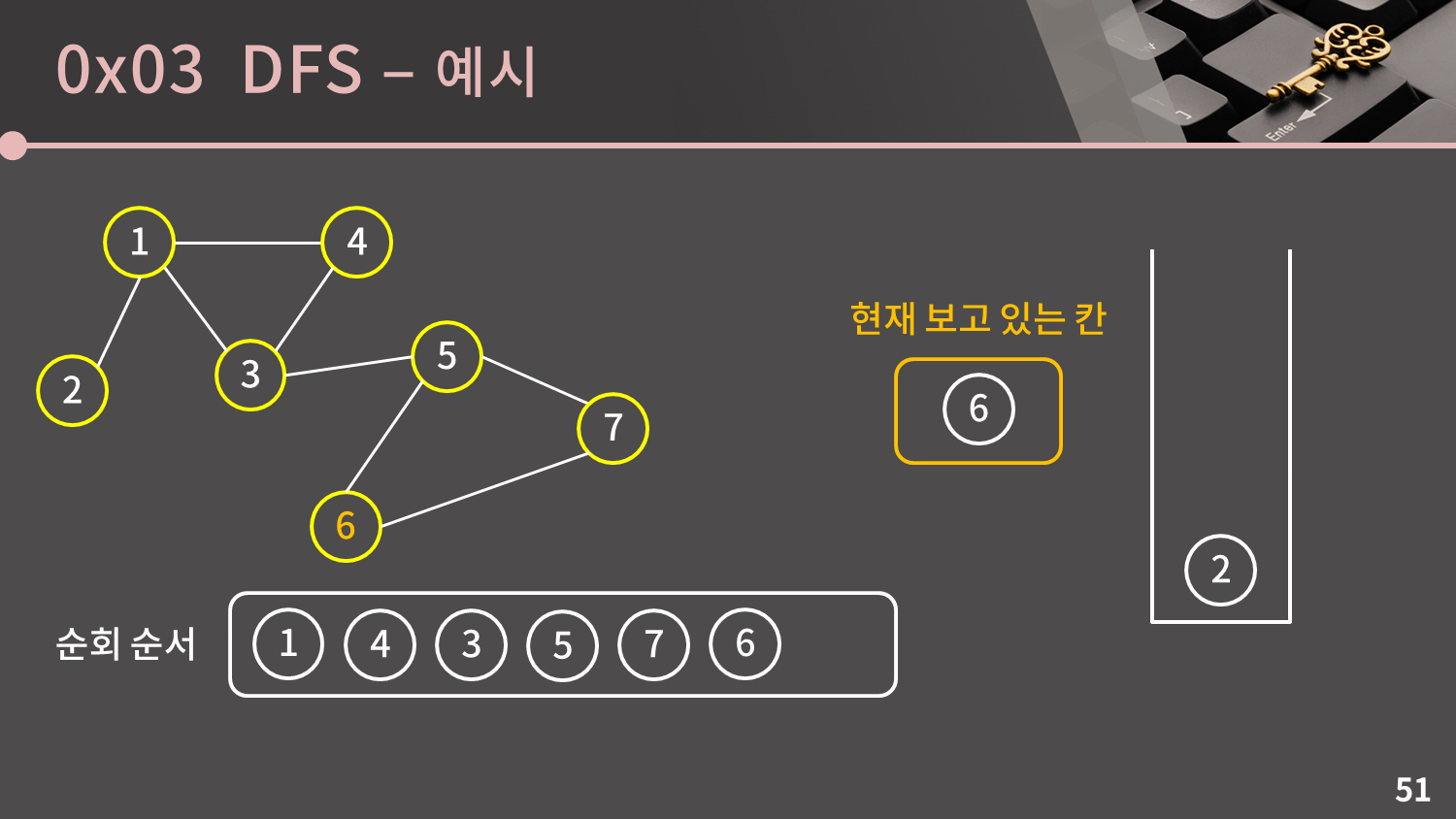
스택이 비어있지 않으므로 스택의 top인 6번 정점을 꺼냅니다. 6번 정점과 이웃한 5, 7번 정점은 이미 방문한 정점이므로 넘어갑니다.
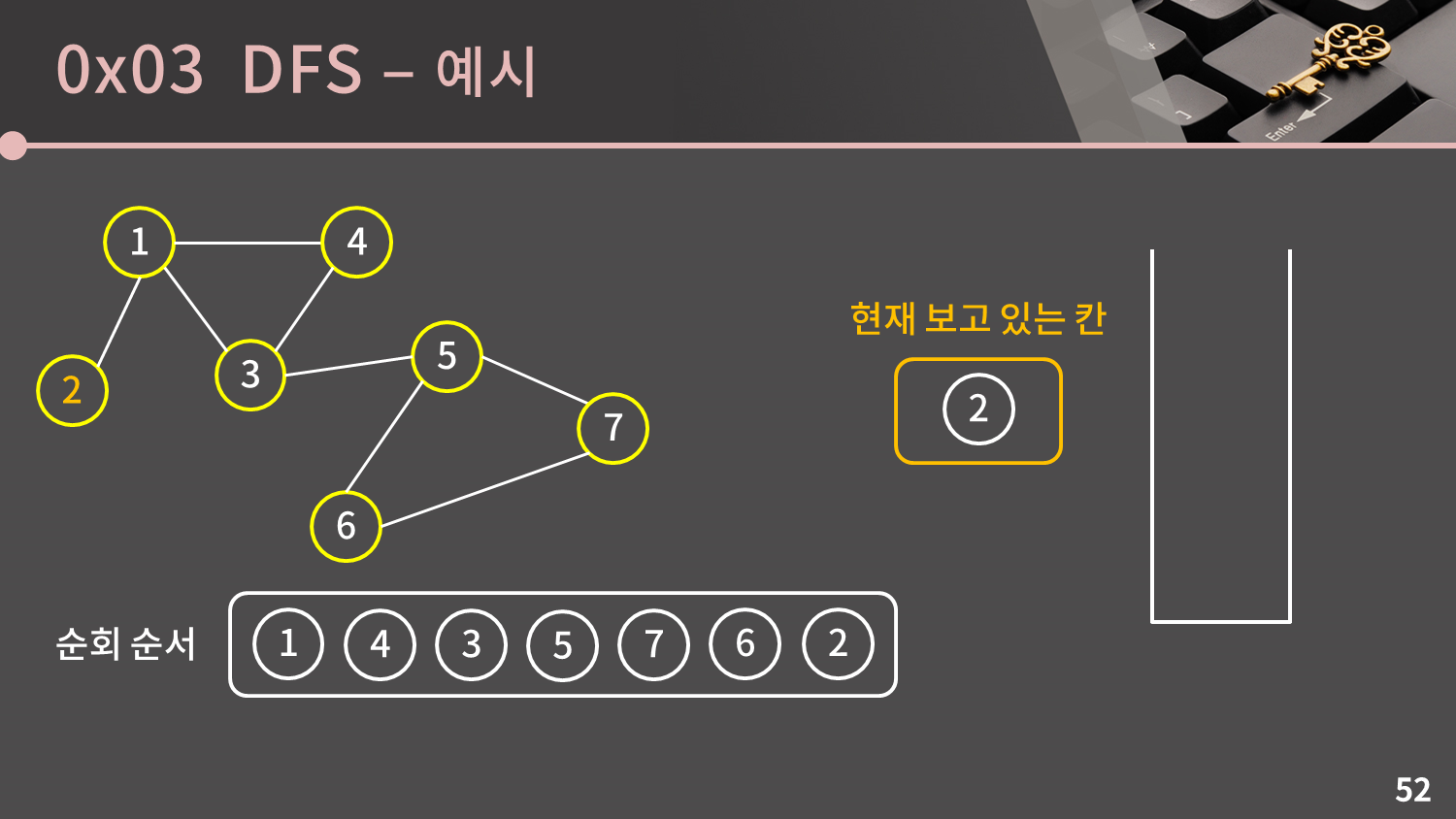
스택이 비어있지 않으므로 스택의 top인 2번 정점을 꺼냅니다. 2번 정점과 이웃한 1번 정점은 이미 방문한 정점이므로 넘어갑니다.

스택이 비었으므로 DFS가 종료됩니다.
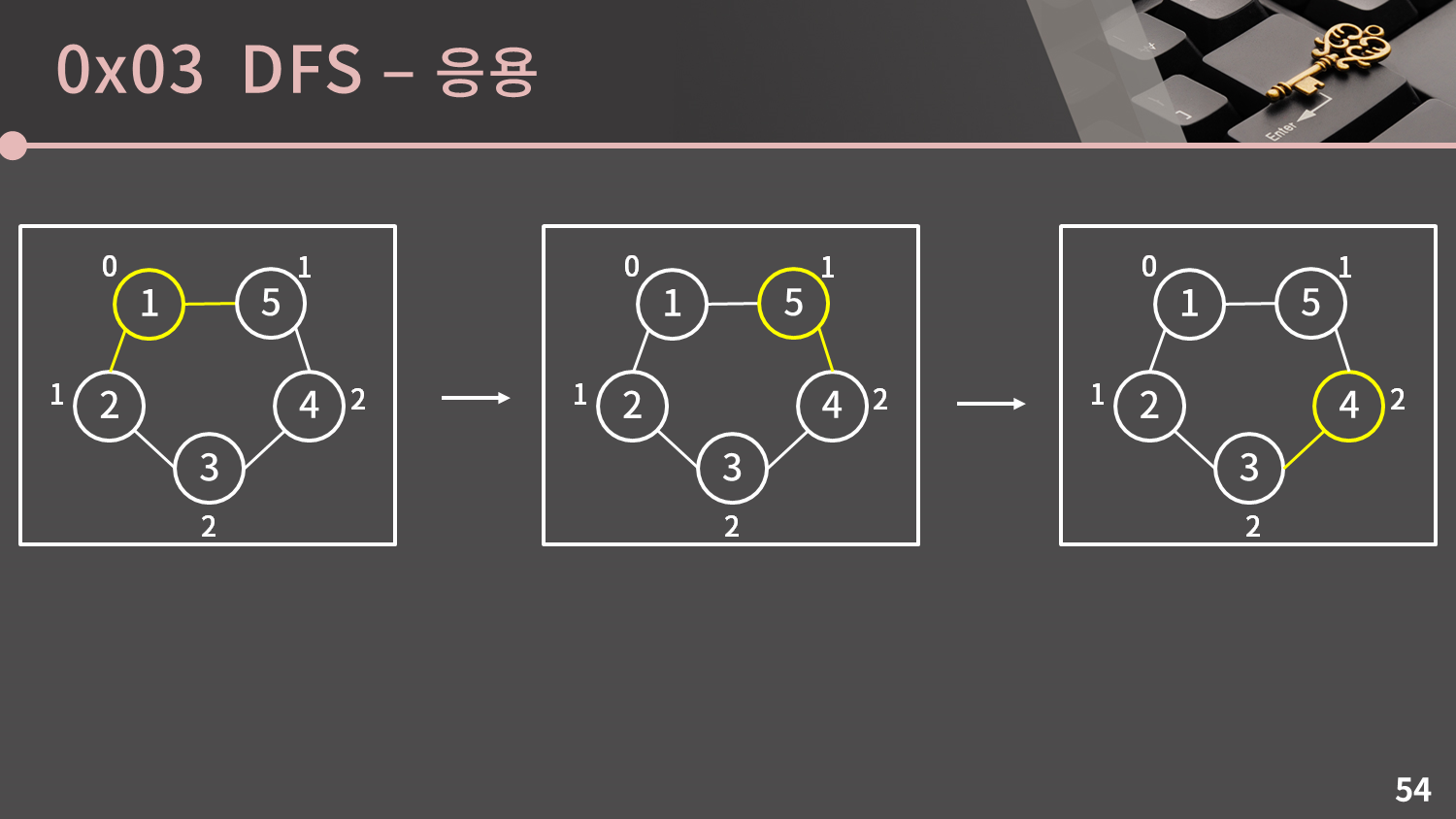
2차원 배열의 DFS와 마찬가지로 그래프의 DFS는 시작점으로부터의 거리를 알아낼 때 사용할 수 없습니다.
위와 같은 그래프에서 DFS를 돌리면 BFS와는 다르게 DFS의 과정 속에서 현재 보는 정점으로부터 추가되는 인접한 정점은 시작점으로부터 1만큼 더 떨어져 있다는 성질이 만족되지 않음을 알 수 있습니다.

이 예시 코드는 순회만 하는 코드입니다. 인접 리스트 방식으로 그래프가 저장되어 있고 정점은 1번부터 순차적으로 매겨져있다고 가정합니다.
큐 대신 스택을 사용했다는 것만 BFS와 차이가 있고 코드의 흐름은 동일합니다.

DFS는 재귀를 이용해서도 구현할 수 있습니다. 재귀적으로 함수를 호출하는 것 자체가 자연스럽게 스택을 이용하는 모양새가 되기 때문에 별도로 스택을 선언할 필요가 없어집니다.
재귀적으로 구현을 한다면 함수 인자로 현재 노드의 번호를 입력받게 되는데, 이 때 만약 1번 노드부터 시작하고자 한다면 vis[1]을 true로 만들어놓고 dfs(1)을 호출해야함에 주의해야합니다.
재귀로 구현을 하게 되면 코드가 알아보기 쉽고 타이핑도 덜 낭비할 수 있습니다. 그러나 스택 메모리의 제한이 작은 경우 재귀 구현에는 아주 큰 문제가 있는데, 재귀적으로 들어갈 때 마다 메모리 중 스택 영역에 계속 데이터가 쌓이게 된다는 점입니다.
예를 들어 그래프가 1 -> 2 -> 3 -> ... -> 100,000 과 같이 일자로 생겨있다고 하면 dfs 재귀 구현에서는 dfs(1) -> dfs(2) -> dfs(3) -> ... -> dfs(100,000)으로 호출이 진행될 것입니다. 이렇게 되면 스택 영역에 최대 함수 100,000개의 데이터가 쌓이게 됩니다.
원래라면 이것은 256MB나 512MB 제한에 전혀 걸리지 않습니다. 그러나 온라인 저지중에 스택 영역의 메모리를 1MB로 제한하는 저지가 있고 대표적으로 현재(=2019년 12월 기준) SW Expert Academy가 그렇습니다. 스택 메모리가 1MB로 제한될 경우 깊이 10만의 재귀 함수는 반드시 스택 메모리 크기 제한을 넘기게 되고, 이로 인해 런타임에러가 발생합니다. 아마 삼성에서 주관하는 코딩테스트에서도 동일한 플랫폼을 사용할 것이기에 마찬가지로 스택 메모리 제한이 1MB일 것입니다.
왜 굳이 스택 영역의 메모리를 1MB로 제한하는지는 모르겠지만 어쨌든 스택 메모리의 제한이 1MB인 곳에서는 재귀 대신 그냥 stack STL 혹은 직접 구현한 stack을 이용해 DFS를 도는 것이 바람직합니다.
참고로 백준 온라인 저지에서는 별도의 스택 메모리 제한은 존재하지 않아 재귀적으로 구현해도 상관없습니다.
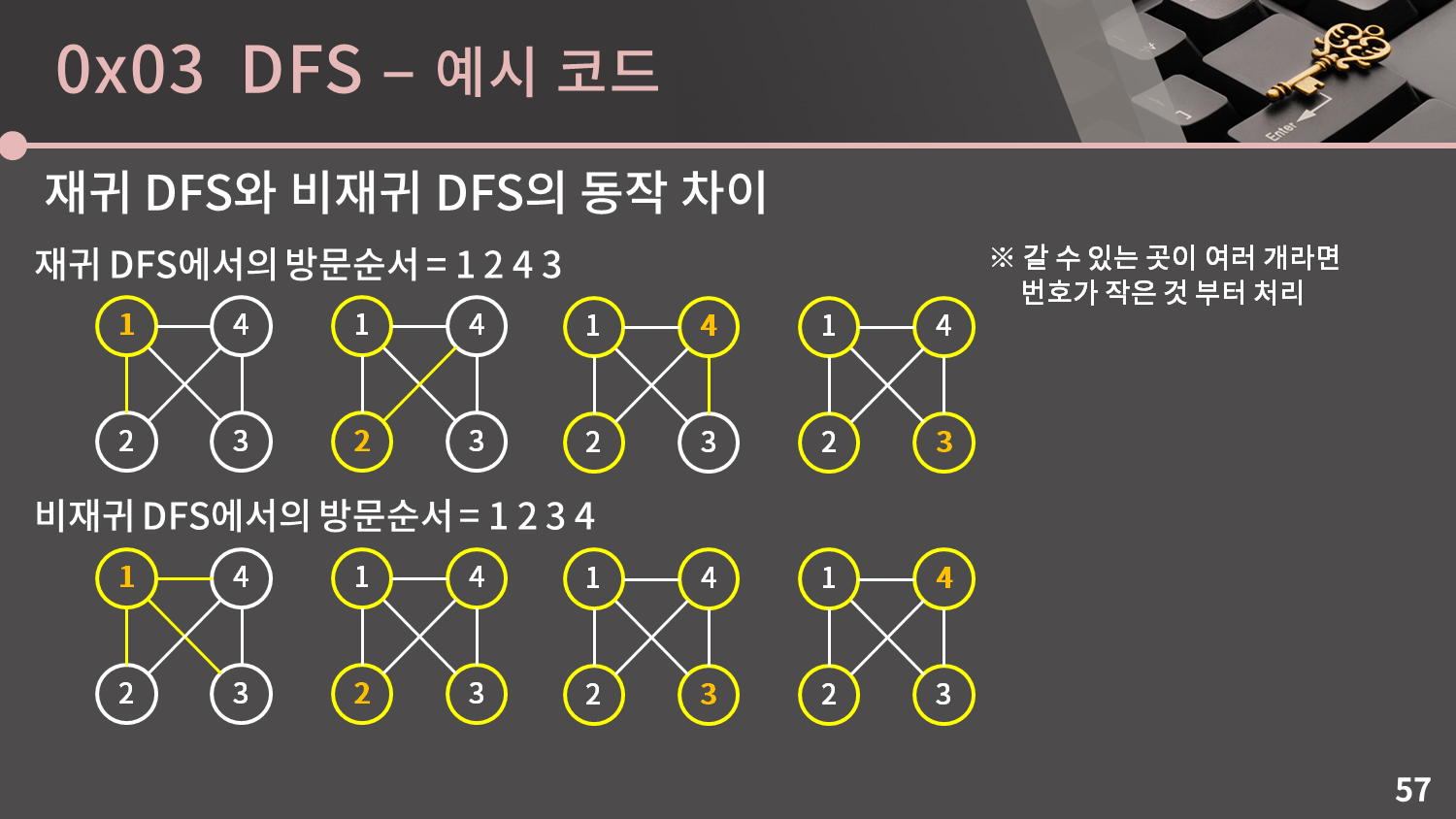
이처럼 DFS를 구현하는 방식을 크게 재귀를 사용하는 방식과 재귀를 사용하지 않는 방식으로 나눌 수 있습니다.
두 방식 모두 특정 정점으로 시작해 도달할 수 있는 모든 정점을 순회하는 역할을 잘 수행합니다.
그러나 둘은 실제 동작에서 약간의 차이가 있는데, 위의 예시를 한번 봅시다.
위와 같은 그래프에서 재귀적인 방식으로 DFS를 돌면 1 2 4 3 순으로 방문을 합니다. 그러나 비재귀적인 방식으로 DFS를 돌면 맨 처음 1번 정점을 스택에서 뽑았을 때 이웃한 2, 3, 4번 정점에 모두 방문했다는 기록을 남겨놓고 다음 정점으로 넘어가기 때문에 1 2 3 4 순으로 방문을 하게 됩니다.
즉 재귀적인 방식과 비재귀적인 방식은 방문했다는 기록을 언제 남기냐에 대한 차이가 있습니다.
엄밀히 말해 우리가 관념적으로 생각하는 DFS는 비재귀 DFS가 동작하는 방식과는 차이가 있고 재귀 DFS가 동작하는 방식과 일치합니다. 미로를 가지고 비유하면 미로를 탈출하기 위해 갈림길에서 갈 수 있는 아무 방이나 찍어 쭉쭉 들어가다가 더 이상 갈 수 없으면 되돌아오는 것이 관념적으로 생각하는 DFS이자 재귀 DFS이지 갈림길에서 다른 방들에는 마크를 두고 한 방만 정해서 들어가는 방식은 아니기 때문입니다.
다시 한 번 강조하면 비재귀 DFS는 순회를 잘 수행하지만 우리가 관념적으로 생각하는 DFS와 세부 동작이 다릅니다. 그래서 단순히 Flood Fill 내지는 순회를 하는 것이 아니라 DFS의 고유한 성질을 사용해 문제를 해결해야 하는 상황일 경우 앞에서 소개한 비재귀 코드를 이용하면 안됩니다.

그러나 비재귀 또한 우리가 관념적으로 생각하는 DFS와 동일하게 동작하도록 바꿀 수 있습니다.
이전 비재귀 DFS 코드에서는 스택에 넣은 직후에 방문 여부를 true로 만들어 스택에 각 정점이 무조건 1번씩만 들어가도록 만들었습니다. 이를 stack에서 값을 뽑은 후에 방문 여부를 true로 만들도록 수정하면 우리가 관념적으로 생각하는 DFS와 동작이 일치하게 됩니다.
스택 자체에는 각 정점이 무조건 1번씩 들어가지는 않고 여러 번 들어갈 수도 있지만 09번 줄의 처리로 인해 연결된 정점을 훑는 작업을 각 정점마다 1번씩 하기 때문에 시간복잡도는 동일하게 $O(V+E)$입니다.
만약 실수로 09번 줄을 빼먹는다면 코드의 시간복잡도가 굉장히 안좋아지거나 무한루프에 빠질 수 있게 됩니다. 이런 경우 제출했을 때 시간 초과 혹은 스택에 push가 계속 일어남으로서 메모리 초과가 발생하게 됩니다.
혹시 이전 슬라이드와 이번 슬라이드에서 다루는 내용이 잘 이해가지 않는다면 그냥 본인에게 편한 비재귀 방식 하나만을 익혀두고 넘어가셔도 상관없습니다. DFS의 고유한 성질을 사용해서 해결해야 하는 문제는 cycle detection, scc, bcc, Eulerian trail 등과 같이 코딩테스트에서는 나올 확률이 0에 수렴하는 어려운 문제들이기 때문입니다.
어차피 코딩테스트 레벨에서는 그래프에서의 flood fill 정도만을 요구할 것이기 때문에 DFS, BFS를 가리지 않고 순회만 할 수 있으면 크게 문제가 없을 것입니다.
참고로 개인적으로는 코드가 짧다는 이유로 그래프에서 재귀적으로 DFS를 하는 것을 선호합니다.

DFS도 마찬가지로 아직 방문하지 않은 시작점에서 DFS를 돌리는 방식으로 연결 그래프가 아닐 때 순회를 처리할 수 있습니다.

마지막으로 연습 문제 2개를 살펴보겠습니다. 첫 번째 문제는 BOJ 11724번: 연결 요소의 갯수 입니다. 문제를 확인해보시면 알겠지만 Undirected Graph에서 연결 요소의 갯수를 구하는 문제입니다.
그래프가 연결 그래프가 아닐 때 순회하던 방식을 조금 응용해 새로운 시작점이 나올 때 마다 카운트를 증가시키는 방식으로 해결이 가능합니다. (정답 코드)

두 번째 문제는 BOJ 1260번: DFS와 BFS 입니다. 이 문제에서는 DFS와 BFS를 실제로 돌도록 요구합니다.
방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문한다는 조건을 맞추기 위해 adj를 정렬하는 과정이 추가로 들어가있습니다. 이외에는 위에서 썼던 코드를 그대로 활용하면 됩니다. 비재귀 버전과 재귀 버전의 코드를 다 두었으니 정답 코드를 확인해보시고 또 직접 구현해보세요. (정답 코드 - 비재귀, 정답 코드 - 재귀)

이번 강의를 통해 여러분은 그래프의 표현법을 익혔고 그래프에서 BFS/DFS를 할 수 있게 되었습니다.
엄밀히 말해 2차원 배열에서 DFS 혹은 BFS를 하도록 요구하는 문제는 끝도 없이 쌓여있지만 그래프에서 단순하게 DFS, BFS만을 하도록 요구하는 문제는 별로 없습니다. 다만 앞으로 Floyd, Dijkstra, Bellman-Ford와 같은 알고리즘을 익힐 때 그래프를 알고 있어야 하기 때문에 이렇게 한 강의를 할애해 그래프를 설명했던 것입니다.
보통 그래프와 관련해 BCC, SCC, DFS Tree 정도는 학교 수업시간에 다루는 경우도 있습니다만 코딩테스트에 나오기에는 고난이도의 문제라고 생각이 들어 적지 않았습니다. 위상 정렬과 최소 신장 트리(Minimum Spanning Tree)는 다다음 강에서 소개를 할 계획입니다.
끝으로 연습 문제를 그룹 내 문제집에 두었으니 풀어보세요.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x12강 - 최소 신장 트리_구버전 (18) | 2020.01.27 |
|---|---|
| [실전 알고리즘] 0x11강 - 위상 정렬_구버전 (13) | 2020.01.17 |
| [실전 알고리즘] 0x10강 - 트리_구버전 (16) | 2019.12.28 |
| [실전 알고리즘] 0x0E강 - 문자열(KMP, 라빈 카프)_구버전 (23) | 2019.07.01 |
| [실전 알고리즘] 0x0D강 - 해쉬, 이진 검색 트리, 힙_구버전 (23) | 2019.06.28 |
| [실전 알고리즘] 0x0C강 - 이분탐색_구버전 (13) | 2019.03.18 |