
안녕하세요, 바킹독이에요. 배열은 복습 잘 하셨나요? 이번 시간에는 연결 리스트라는 것을 같이 배워보겠습니다.

배열에서 한 것 처럼 연결 리스트가 무엇인지 알아보고, 같이 구현해볼 것입니다.
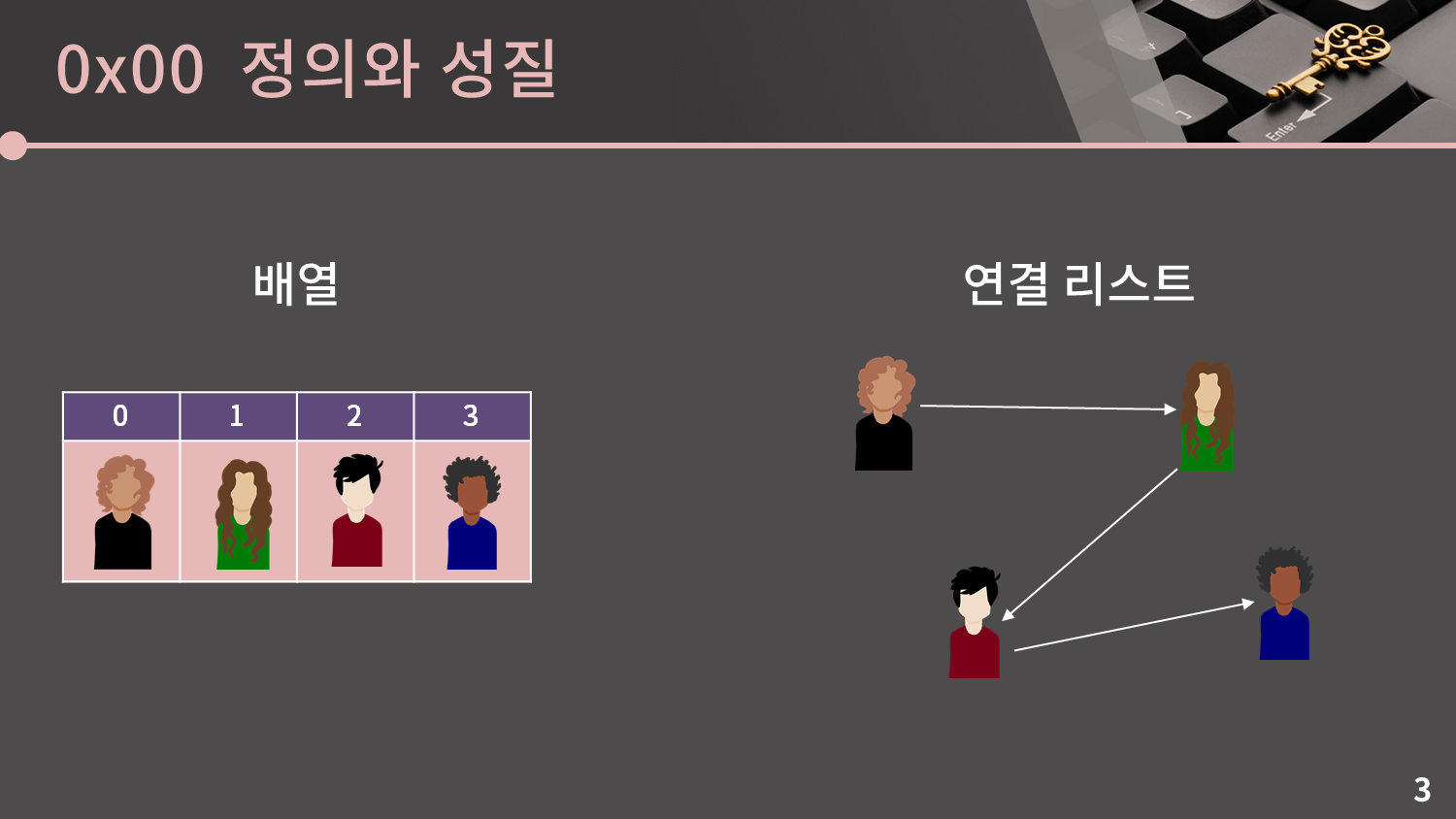
연결 리스트가 무엇인가 하면, 원소들을 저장할 때 그 다음 원소가 있는 위치를 포함시키는 방식으로 저장하는 자료구조입니다. 원소들은 이곳 저곳에 흩어져있습니다.
실생활의 예시를 들어보자면, 제가 학교 선생님이고 전체 학생 중에서 영은, 현지, 재현, 상혁 학생 4명을 술래로 정했고, 이 4명을 기억하고 싶습니다. 이런 상황일 때 배열이라면 그냥 4칸짜리 배열을 만들고 4명을 저장하면 될 것입니다.
그런데 연결 리스트의 관점에서는 영은이가 현지를 기억하고, 현지는 재현이를 기억하고, 재현이는 상혁이를 기억하는 것입니다. 이렇게 되면 저는 영은이만 외우고 있어도 됩니다. 그리고 4명 전체가 필요하면 저는 영은이를 통해 나머지 3명이 누구였는지를 알아낼 수 있게 됩니다.
이전에 연결 리스트를 전혀 접해본 적이 없다면 비유를 보고도 무슨 말인지 영 감이 오지 않을 수도 있는데, 강의 내용을 따라가다보면 자연스럽게 이해가 될거여서 크게 걱정하실 필요는 없습니다.
자 그러면 연결 리스트의 성질이 어떤지를 한 번 보겠습니다. 배열과 연결 리스트를 비교하는 경우가 많기 때문에 배열에서는 어땠는지를 떠올리면서 봐도 좋습니다.
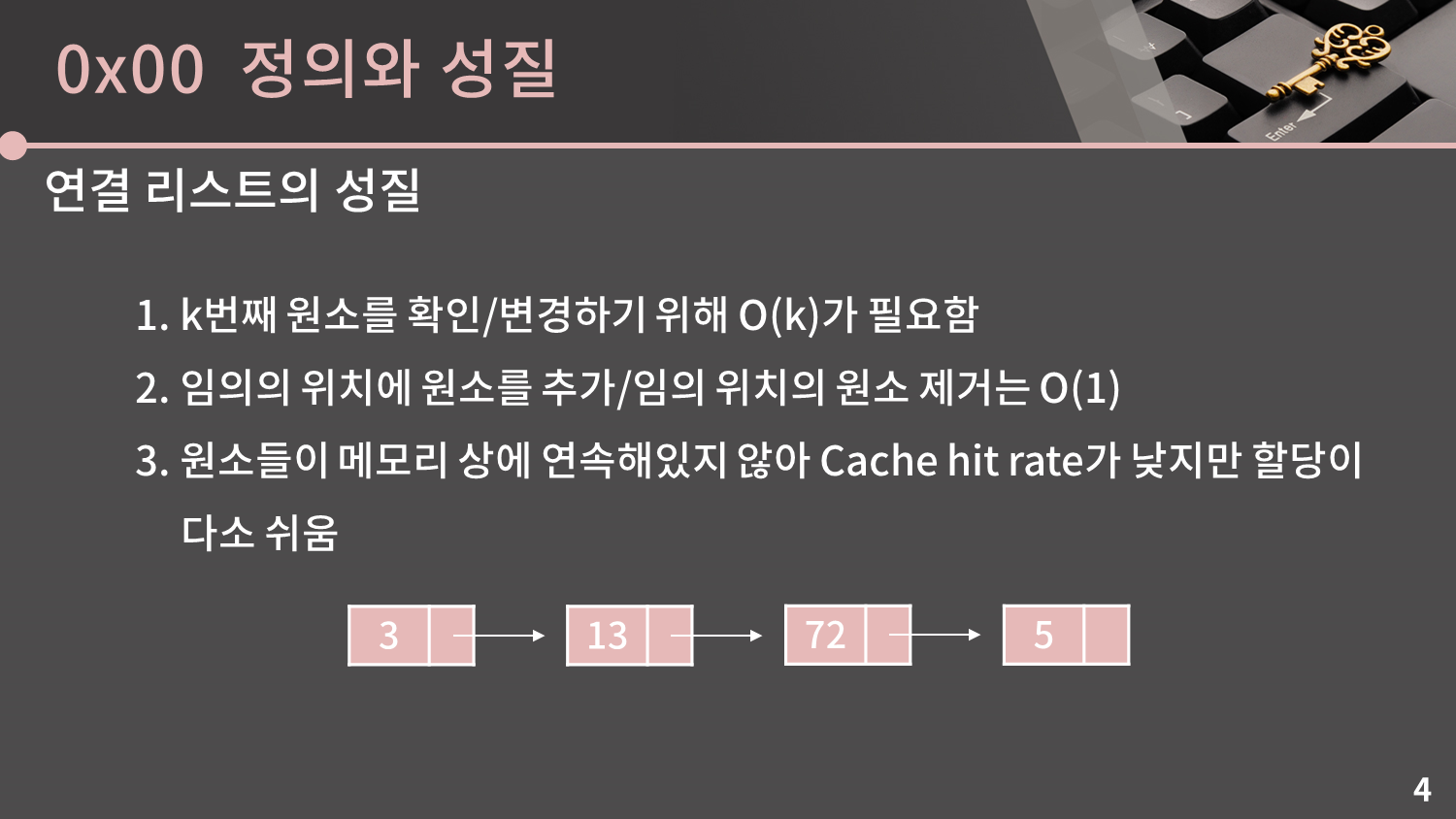
첫 번째로 연결 리스트에서는 k번째 원소를 찾기 위해 O(k)의 시간이 필요합니다. 뭔가 좀 의아할 수 있는데, 연결 리스트의 구조 상 어쩔 수가 없습니다. 지금 이 그림은 3, 13, 72, 5를 저장하는 연결 리스트입니다. 여기서 3번째 원소인 72를 찾고 싶으면 3을 거쳐서 13을 가고, 13을 거쳐서 72를 가야하기 때문에 그렇습니다. 이렇게 가지 않고서는 72가 대체 어디 있는지 알 방법이 없습니다. 배열과 다르게 공간에 원소들이 연속해서 위치하고 있지 않기 때문입니다.
두 번째로 연결 리스트에서는 임의의 위치에 원소를 추가하거나 임의 위치의 원소 제거가 O(1)입니다. 이 성질이 배열과 비교했을 때 큰 차이가 있는 성질이고, 연결 리스트의 굉장히 큰 장점이기도 합니다. 이 부분은 직접 기능을 살펴볼 때 자세하게 설명을 드리겠습니다.
세 번째로 메모리 상에 데이터들이 연속해있지 않으니까 Cache hit rate가 낮지만 할당이 쉽습니다. 물론 이 성질은 코딩테스트를 칠 때는 몰라도 상관없습니다.

배열과는 다르게 연결 리스트에는 몇 개 종류가 있는데 같이 한 번 살펴보겠습니다.
첫 번째는 단일 연결 리스트입니다. 단일 연결 리스트는 각 원소가 자신의 다음 원소의 주소를 들고 있는 연결 리스트입니다.
두 번째는 이중 연결 리스트입니다. 이중 연결 리스트에서는 각 원소가 자신의 이전 원소와 다음 원소의 주소를 둘 다 들고 있습니다. 단일 연결 리스트에서는 주어진 원소의 이전 원소가 무엇인지를 알 수 없는데 이중 연결 리스트에서는 알 수 있습니다. 다만 원소가 가지고 있어야 하는 정보가 1개 더 추가되니 메모리를 더 쓴다는 단점이 있습니다. 참고로 STL에 연결 리스트가 있는데, 이 컨테이너의 이름은 list이고 구조는 이중 연결 리스트입니다.
세 번째는 원형 연결 리스트입니다. 원형 연결 리스트에서는 끝이 처음과 연결되어 있습니다. 그림의 예시는 단일 연결 리스트로 표현했지만 각 원소가 이전과 다음 원소의 주소를 모두 들고 있어도 상관이 없습니다.

배열과 연결 리스트는 메모리 상에 원소를 놓는 방법은 다르다고 해도 어찌됐든 원소들 사이의 선후 관계가 일대일로 정의가 됩니다. 즉, 원소들 사이에서 첫 번째 원소, 두 번째 원소, … 이런 개념이 존재하는 것입니다.
그래서 배열과 연결 리스트는 선형 자료구조라고 불립니다. 까마득한 후에 배우게 될 트리, 그래프, 해쉬 등은 비선형 자료구조의 대표적인 예시입니다.
배열과 연결 리스트는 둘 다 선형 자료구조여서 면접에서 둘의 비교하는 문제를 구술 시험으로 내기도 합니다. 꼭 면접 대비가 아니라고 하더라도 둘의 차이를 잘 알아야 적재적소에 배열이나 연결 리스트를 잘 써먹을 수 있을테니 둘의 장단점을 비교하는 시간을 가져보도록 하겠습니다.
첫 번째로 k번째 원소의 접근은 배열의 경우 O(1), 연결 리스트의 경우 O(k)입니다.
두 번째로 임의 위치에 원소를 추가하거나 제거하는건 배열의 경우 O(N), 연결 리스트의 경우 O(1)입니다. 그런데 엄밀히 말해서 연결 리스트에서도 3번째 원소 뒤에 20이라는 원소를 추가하고 싶다고 하면, 일단 3번째 원소까지는 찾아간 뒤에야 O(1)에 추가가 가능한거라 상황이 조금 다르긴 한데, 이건 구현 파트에서 자세하게 다루겠습니다.
메모리 상의 배치는 배열의 경우 연속이고 연결 리스트의 경우 불연속입니다. 마지막으로 추가적으로 필요한 공간, 즉 overhead를 생각해보면 배열은 데이터만 딱딱 저장하면 될 뿐 딱히 추가적으로 필요한 공간이 없습니다. 굳이 따지면 길이 정보를 저장할 int 1개가 필요할 수 있지만 이건 너무 미미하니 신경을 쓸 필요가 없을 정도입니다. 그런데 연결 리스트에서는 각 원소가 다음 원소, 혹은 이전과 다음 원소의 주소값을 가지고 있어야 합니다. 그래서 32비트 컴퓨터면 주소값이 32비트(=4바이트) 단위이니 4N 바이트가 추가로 필요하고, 64비트 컴퓨터라면 주소값이 64비트(=8바이트) 단위이니 8N 바이트가 추가로 필요하게 됩니다. 즉 N에 비례하는 만큼의 메모리를 추가로 쓰게 됩니다.


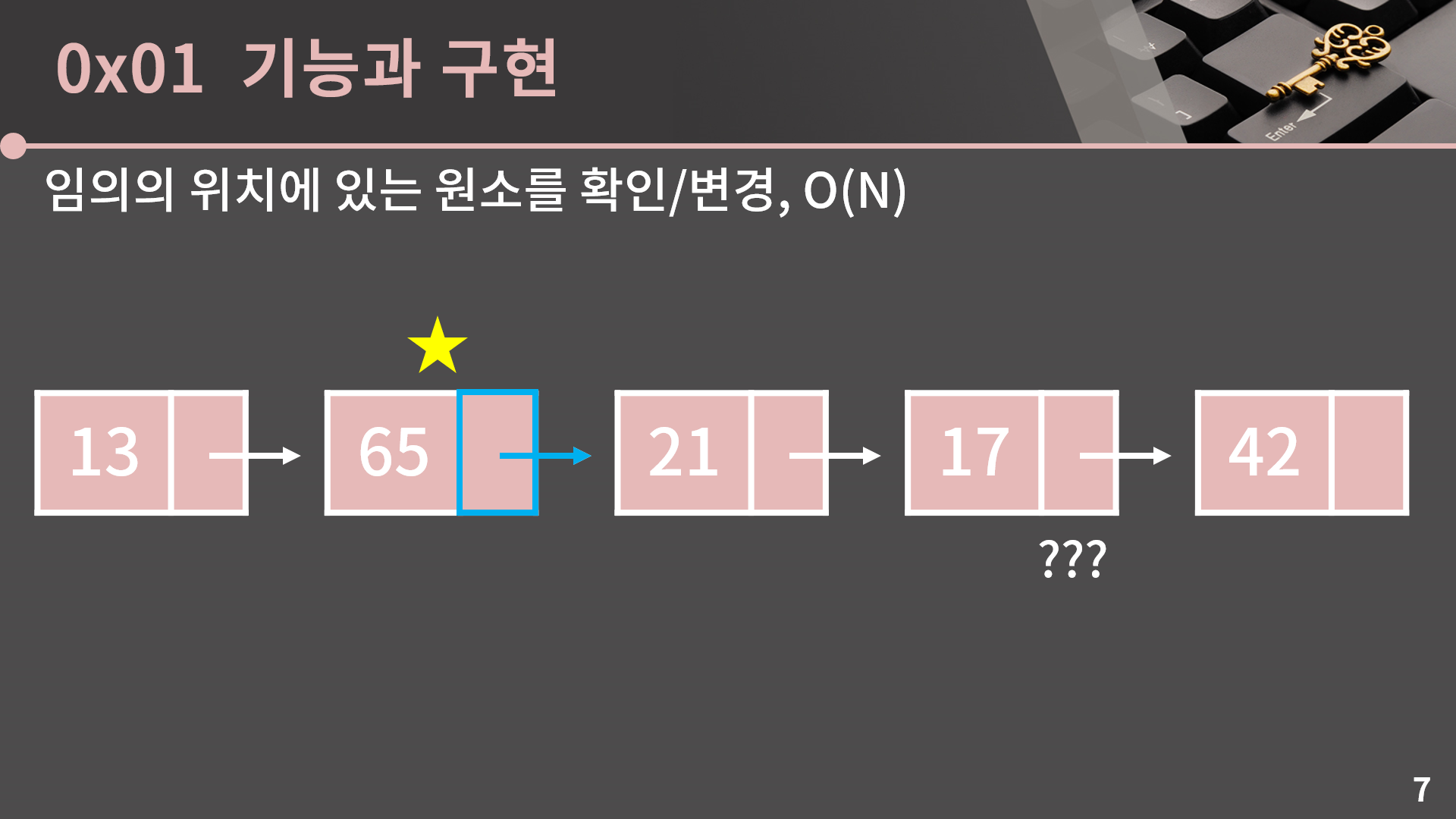

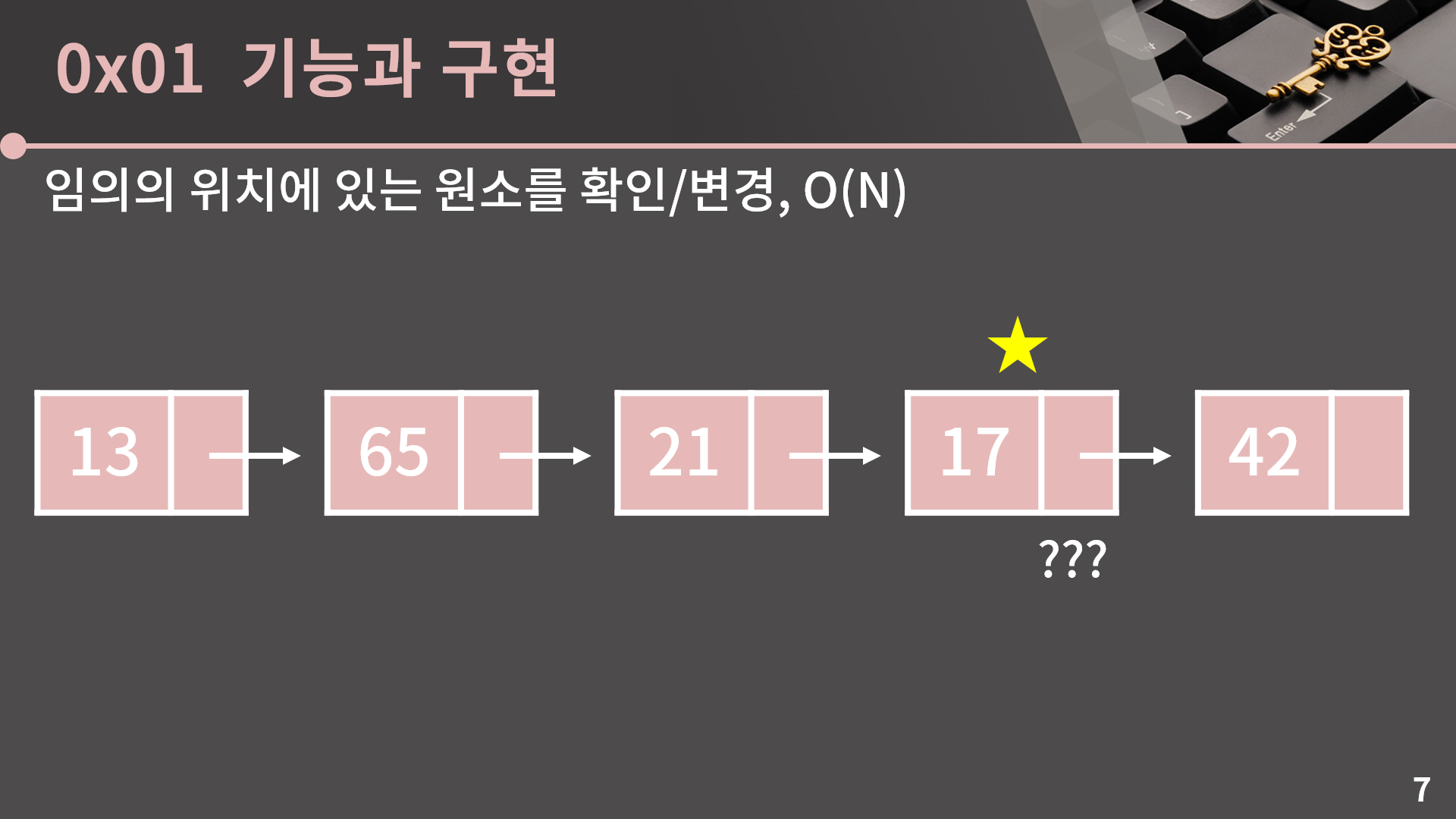
이제 연결 리스트에서 제공되는 연산들을 하나씩 살펴보겠습니다. 첫 번째로 임의의 위치에 있는 원소를 확인/변경하는 연산인데, 계속 언급했듯이 배열과는 다르게 임의의 위치에 있는 원소로 가기 위해서는 그 위치에 도달할 때 까지 첫 번째부터 순차적으로 방문을 해야 합니다.
이건 연결 리스트의 구조 상 어쩔 수 없는건데, 분명 모든 원소들은 메모리 어딘가에 있을테지만, 우리는 그 중에서 첫 번째 원소의 주소만 알고 있습니다. 그러면 우리가 네 번째 원소의 값을 확인하고 싶다고 할 때, 우리는 첫 번째 원소에 기록된 주소를 보고 두 번째 원소로 넘어가고, 두 번째 원소에 기록된 주소를 보고 세 번째 원소로 넘어가고, 세 번째 원소에 기록된 주소를 보고 네 번째 원소로 넘어가서 드디어 도착했습니다.
그렇기 때문에 k번째 원소를 보기 위해서는 O(k)의 시간이 필요하고, 전체에 N개의 원소가 있다고 하면 평균적으로 N/2의 시간이 걸릴테니 O(N)이라고 생각하면 됩니다.



두 번째로 임의의 위치에 원소를 추가하는 연산인데, 이건 O(1)에 가능합니다. 왜냐하면, 예를 들어 21 뒤에 84를 추가하고 싶다고 할 때, 배열처럼 그 뒤의 원소들을 전부 옮기는 작업을 할 필요가 없고 그냥 21과 84에서 다음 원소의 주소만 변경을 해주면 되기 때문에 그렇습니다.
단, 착각하면 안되는게 있는데, 추가하고 싶은 위치의 주소를 알고 있을 경우에만 O(1)입니다. 만약 21의 주소를 준 것이 아니라 그냥 84라는 원소를 세 번째 원소 뒤에 추가하라는 명령의 경우에는, 세 번째 원소까지 찾아가야 하는 시간이 추가로 걸려서 O(1)이라고 말할 수 없습니다.


마지막으로 임의 위치의 원소를 제거하는 연산이고 이것 또한 O(1)에 가능합니다. 한 번 21을 지워보겠습니다. 21을 지우려고 하면 딱 1개만 하면 되는데, 그냥 65에다가 "너의 다음 원소가 21이 아닌 17이다"라고만 알려주면 끝입니다. 물론 그런 다음에 21이 들어있는 원소는 메모리 누수를 막기 위해 메모리에서 없애줄 필요가 있습니다.

정리를 해보면 임의의 위치에 있는 원소를 확인하거나 변경하는건 O(N)이고, 해당 위치의 주소를 같이 넘겨줄 때 임의의 위치에 원소를 추가하거나 임의 위치의 원소를 제거하는건 O(1)입니다.
저희가 지금 연결 리스트를 다루고는 있는데, 배열이 너무 익숙하다보니 도대체 임의의 위치에 있는 원소를 확인/변경하는게 O(N)인 이런 자료구조를 어디에 써먹을 수 있나 싶겠지만 연결 리스트가 쓰이는 대표적인 상황이 바로 메모장과 같은 텍스트 에디터입니다. 물론 실제 텍스트 에디터는 매 순간순간마다 화면에 결과를 출력해야 하니 아마도 그냥 배열로 구현을 할 것 같습니다.
그러나 예를 들어 커서를 옮기고 글자를 지우는 것과 같은 연산들이 다양하게 주어진 후 최종 결과를 출력하라는 문제라고 한다면 우리는 커서가 가리키는 위치에 글자를 추가하거나 글자를 지우는 명령을 계속 수행해야 합니다. 이런 경우에 배열은 임의의 위치에 글자를 추가하는 연산이 비효율적인데 연결 리스트에서는 O(1)에 처리할 수 있어서 연결 리스트로 구현할 경우에 효율적일 수 있습니다.
그러니까 임의의 위치에서 원소를 추가하거나 임의 위치의 원소를 제거하는 연산을 많이 해야 할 경우에는 연결 리스트의 사용을 고려해보면 좋습니다.

자료구조를 배웠으니 구현을 안할 수가 없는데, 원래 연결 리스트의 정석적인 구현은 지금 보시는 것 처럼 NODE 구조체나 클래스를 만들어서 원소가 생성될 때 동적할당을 하는 방식입니다. 이 방식은 학부에서 자료구조 수업을 들으신 분이라면 분명 보셨을 구현이고, 또 면접에서 손코딩을 시킨다거나 하는 식으로 질문을 할 수가 있기 때문에 개인적으로 공부를 하셔야합니다.
그런데 이 구현은 긴박한 코딩테스트에서 쓰기는 별로 좋지가 않습니다. 코딩테스트에서는 그냥 STL list를 활용하면 됩니다. STL list가 Doubly Linked List 구조를 가지고 있기 때문에 연결 리스트가 필요하면 그냥 가져다 쓰면 됩니다. 그런데 코딩테스트에서 STL을 허용하지 않는다면 직접 연결 리스트를 구현해야 합니다. STL을 허용하지 않는 코딩테스트가 정말 드물긴한데, 연결 리스트를 정석적으로 구현하는 대신 야매로 구현하면 구현 난이도가 크게 높지 않아서 연결 리스트를 연습하는 셈 치고 야매 연결 리스트를 소개해드리겠습니다.
그런데 정석적인 구현을 이전에 접해본 적이 없으면 야매 연결 리스트의 구현을 봐도 코드가 어떻게 동작하는지 잘 감이 안올 수도 있습니다. 만약 코딩테스트를 위해서 강의를 듣고 있는데 구현을 봐도 잘 이해가 안간다 싶으면 그냥 넘어가고 STL list의 사용 방법만 제대로 익혀가셔도 괜찮습니다.

그러면 야심차게 준비한 야매 연결 리스트를 소개해드리겠습니다. 이 야매 연결 리스트는 원소를 배열로 관리하고 pre와 nxt에 이전/다음 원소의 포인터 대신 배열 상의 인덱스를 저장하는 방식으로 구현한 연결 리스트입니다. 메모리 누수의 문제 때문에 실무에서는 절대 쓸 수 없는 방식이지만 코딩테스트에서는 구현 난이도가 일반적인 연결 리스트보다 낮고 시간복잡도도 동일하기 때문에 애용하면 됩니다.
구현에 필요한 변수들을 보면 dat[i]는 i번지 원소의 값, pre[i]는 i번지 원소에 대해 이전 원소의 인덱스, nxt[i]는 다음 원소의 인덱스입니다. pre나 nxt의 값이 -1이면 해당 원소의 이전/다음 원소가 존재하지 않는다는 의미입니다. unused는 현재 사용되지 않는 인덱스, 즉 새로운 원소가 들어갈 수 있는 인덱스이고 원소가 추가된 이후에는 1씩 증가될 것입니다. 그리고 특별히 0번지는 연결 리스트의 시작 원소로 고정되어 있습니다. 달리 말하면 0번지는 값이 들어가지 않고 단지 시작점을 나타내기 위한 dummy node입니다.
지금 코드 상에는 별도로 길이 정보를 두지 않았지만 길이가 필요하다면 따로 len 변수를 두고 원소가 추가될 때 1 증가시키고 제거될 때 1 감소시키면 됩니다.

지금 각 변수의 역할이 잘 이해가 안갈 수 있을 것 같습니다. 그래서 실제 연결 리스트가 야매 연결 리스트에서는 어떻게 저장되는지를 예시로 하나 보여드리겠습니다.
주어진 연결 리스트는 13, 65, 21, 17이라는 값을 가지고 있습니다. 그리고 이들은 각각 배열에서 2번지, 1번지, 4번지, 5번지에 저장되어 있다고 생각하겠습니다. 이 위치들은 임의로 정한 위치이고 실제로는 1번지부터 unused가 가리키고 있는 위치 한칸 전까지 사이에서 아무데나 위치하게 됩니다.
그리고 특별히 0번지는 연결 리스트의 시작 원소로 고정되어 있습니다. 즉, 실제로 값이 들어있는 것은 아니지만 관념적으로 연결 리스트의 제일 앞에 원소 하나가 있다고 생각을 할 것입니다. 왜 이렇게 하냐면, 이런 dummy node를 두지 않으면 나중에 삽입과 삭제등의 기능을 구현할 때 원소가 아예 없는 경우에 대한 예외처리를 해야 하는데, 관념적으로 dummy node를 두면 예외처리가 덜 번거로워져서 그렇습니다.
그러면 일단 0번지의 dat, pre, nxt를 보겠습니다. 한 세 번째 강조하고 있는 말이지만 dummy node라 dat는 의미가 없으니 그냥 -1로 두고 pre는 해당 원소의 이전 원소가 존재하지 않으니 -1이고 nxt는 13이 들어있는 주소인 2번지의 2가 됩니다.
그 다음으로 13이 들어있는 2번지의 dat, pre, nxt를 보면 dat는 13, pre는 이전 원소의 주소인 0,(클릭) nxt는 다음 원소의 주소인 1이 됩니다.
나머지들은 크게 어렵지않을 것 같아서 설명을 더 하지 않겠습니다. 직접 손으로 채워넣어보기도 하면서 dat, pre, nxt가 무엇을 의미하는지 정확하게 이해를 하고 계속 진행해주세요.
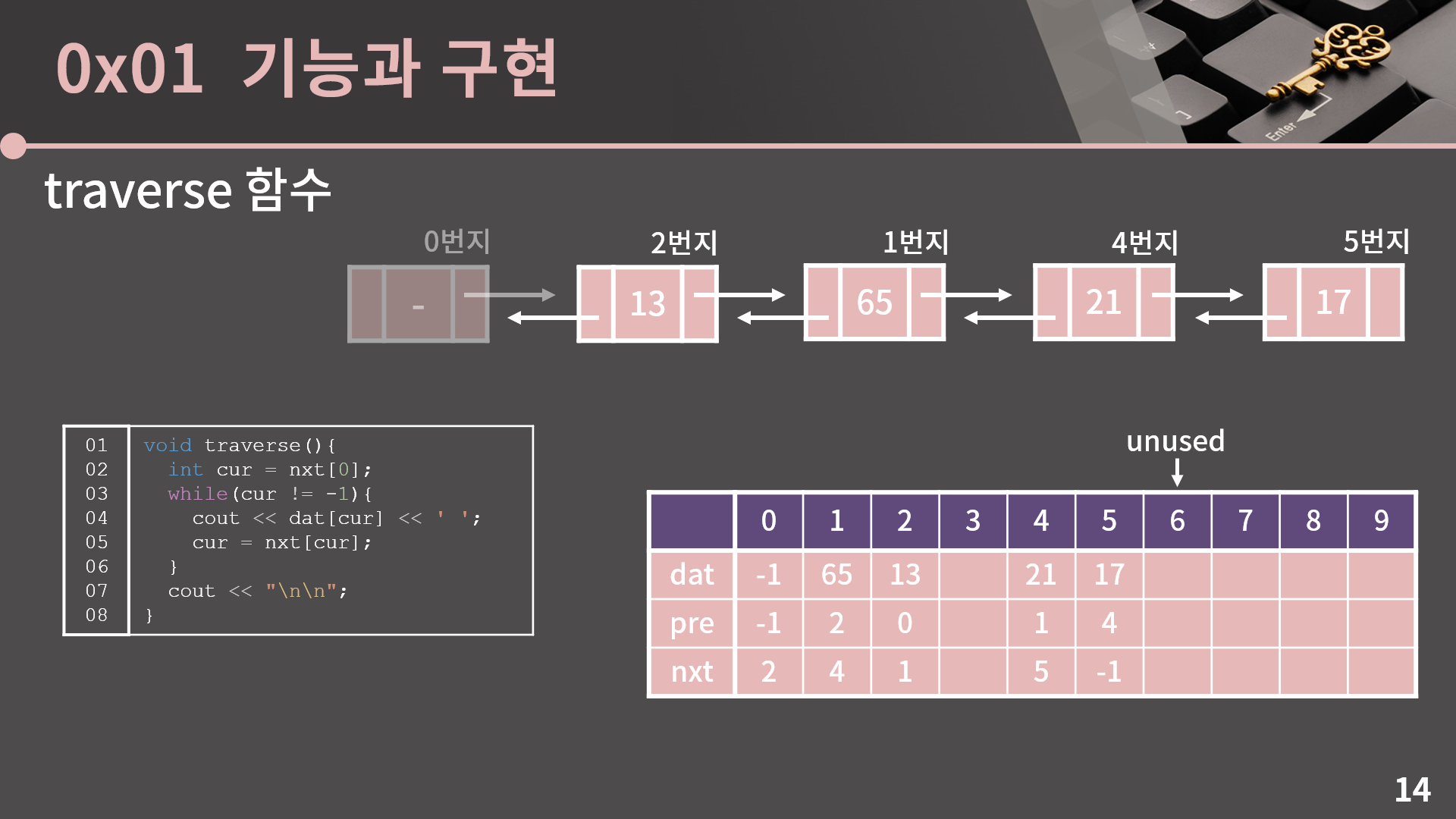
이제 각 기능들을 구현해보는 시간을 가질텐데, traverse 함수는 먼저 같이 구현을 해보겠습니다. traverse 함수에서는 연결 리스트의 모든 원소들을 출력할 것입니다.
배열에서 모든 원소들을 출력할 때에는 그냥 arr[0], arr[1], … 을 출력하면 됐는데 이 야매 연결 리스트에서 만약 dat[0], dat[1], … 을 출력하면 좀 이상할 것입니다.
대신 우리는 0번지에서 출발해 nxt에 적힌 값을 보고 계속 넘어가면서 dat을 출력하는 방식으로 구현해야 합니다. 코드를 보면 cur라는 변수에 각 원소들의 주소가 담겨서 이동하는 방식입니다.
일단 cur의 초기 값으로 nxt[0] = 2가 들어가고 while문이 시작됩니다. 처음으로 dat[2], 즉 13이 출력되고 cur는 2에서 nxt[2] = 1로 넘어갑니다. 그 다음에는 dat[1], 즉 65가 출력되고 cur는 1에서 nxt[1] = 4로 넘어갑니다. 이런식으로 반복되다가 17까지 출력하고, cur에 nxt[5] = -1이 담기면 끝에 도달했다는 것을 깨닫고 while문을 탈출해서 traverse 과정이 종료됩니다.

traverse 함수는 같이 구현을 했고, 남은건 insert와 erase 함수입니다. 할 수 있으면 github 링크에 들어가서 코드를 받은 후에 insert, erase 함수를 채워보세요.
그런데 아무 설명도 안듣고 깡으로 구현하는건 좀 힘들 것 같고, 제가 두 함수 각각을 코드는 안보여드리고 설명만 드릴테니 그 설명을 같이 본 후에 구현을 시도해보셔도 될 것 같습니다. 물론 도전정신이 충만하시면 일단 한 번 시도해보는 것도 정말 환영입니다.
두 함수에 공통으로 있는 인자인 addr는 앞에서 말한 각 원소의 주소, 즉 배열 상에서 몇 번지인지를 의미합니다. 예를 들어 원소 13이 2번지이고 13 뒤에 20을 새로 추가하고 싶은거면 insert(2, 20)을 호출해야 하고, 13을 지우고 싶으면 erase(2)를 호출해야 합니다. addr = 2가 의미하는 것이 연결 리스트 상에서 2번째 원소라는 것이 아니라, 해당 원소의 주소가 2번지라는 점을 꼭 헷갈리면 안됩니다.

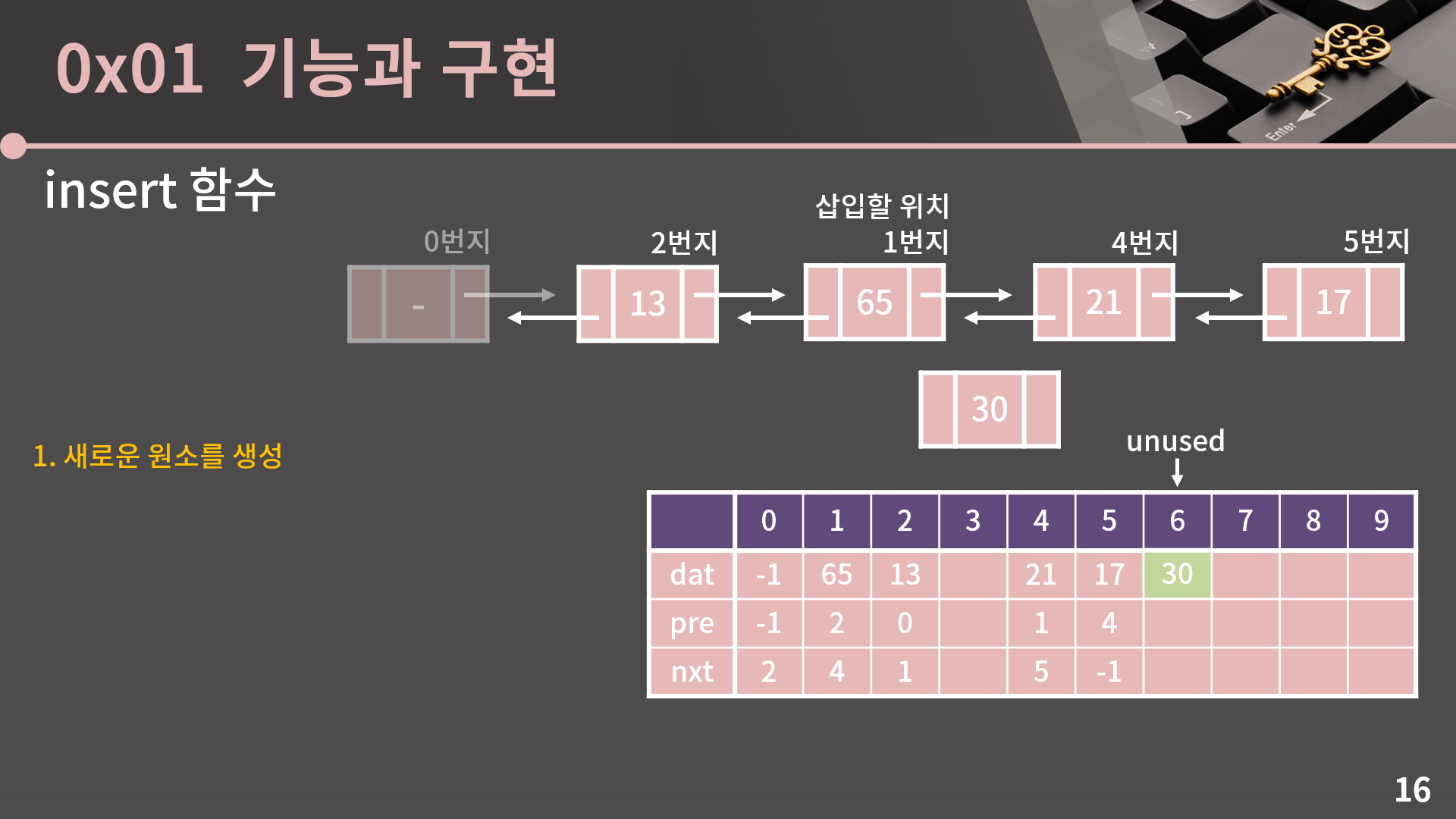
그러면 이제 insert 함수를 설명드리겠습니다. 말씀드렸다시피 코드는 말고 구현 방법만 설명을 드리겠습니다. 저는 65 뒤에 30을 추가하고 싶고, 이 경우에는 65가 1번지이니 insert(1, 30)이 호출됩니다. 설명의 편의를 위해 65를 삽입할 위치라고 부르겠습니다.
첫 번째로 일단 30이 들어갈 새로운 원소를 생성해야 합니다. 어떻게 만드나 궁금할텐데 unused가 가리키는 곳이 바로 새로운 원소가 들어갈 자리입니다. 그 곳의 dat에 30을 쓰면 관념적으로 원소를 생성한 것과 똑같이 됩니다.

두 번째로는 새 원소의 pre 값에 삽입할 위치의 주소, 즉 1번지를 대입해야 합니다.

세 번째로 새 원소의 nxt 값에 삽입할 위치의 nxt값, 즉 4번지를 대입해야 합니다.
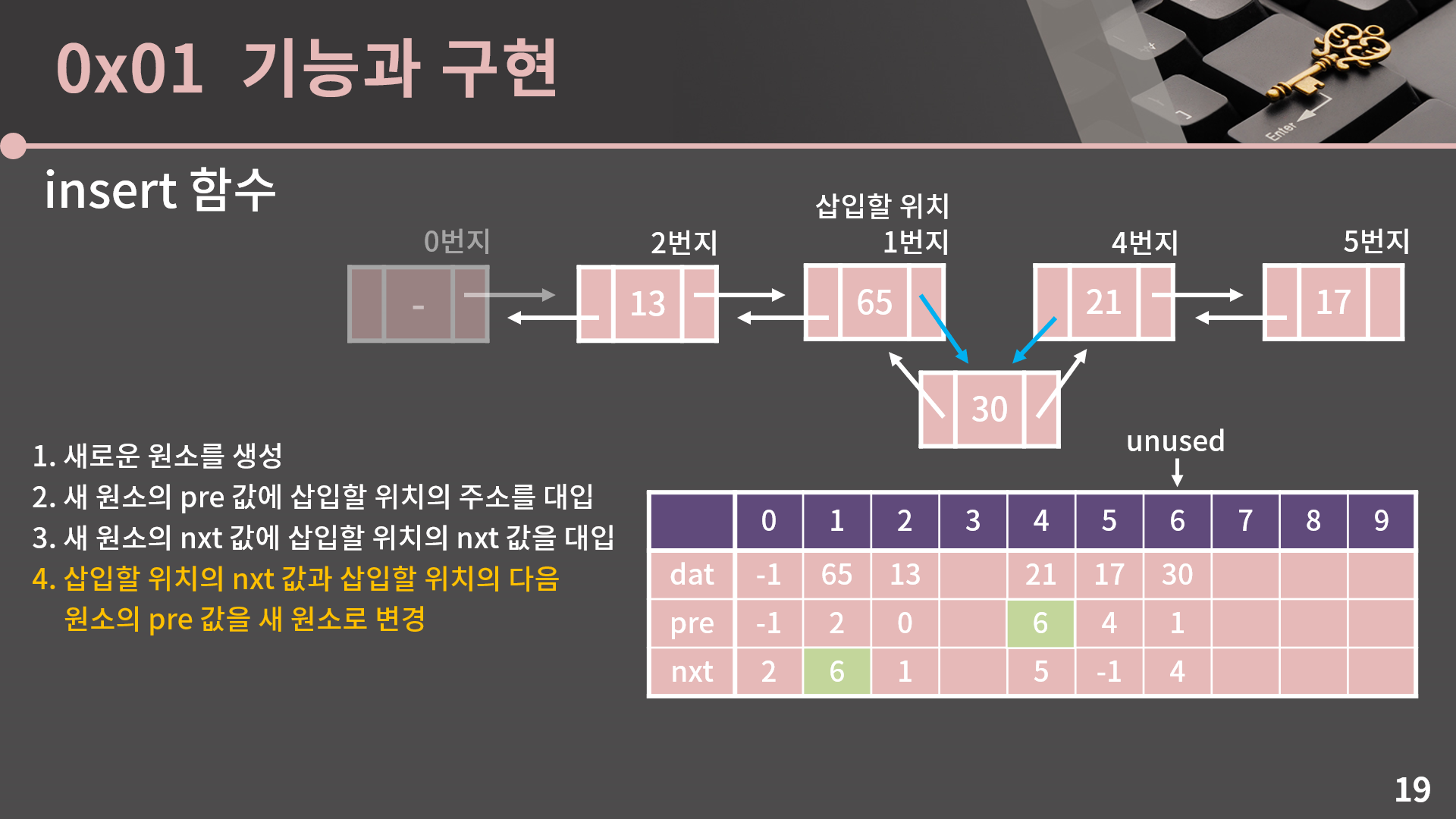
네 번째로 무엇을 해야할지 맞춰봅시다. 그림을 딱 보면 보이는게 있을텐데, 삽입할 위치의 nxt와 삽입할 위치의 다음 원소의 pre를 새 원소로 바꿔야 합니다.
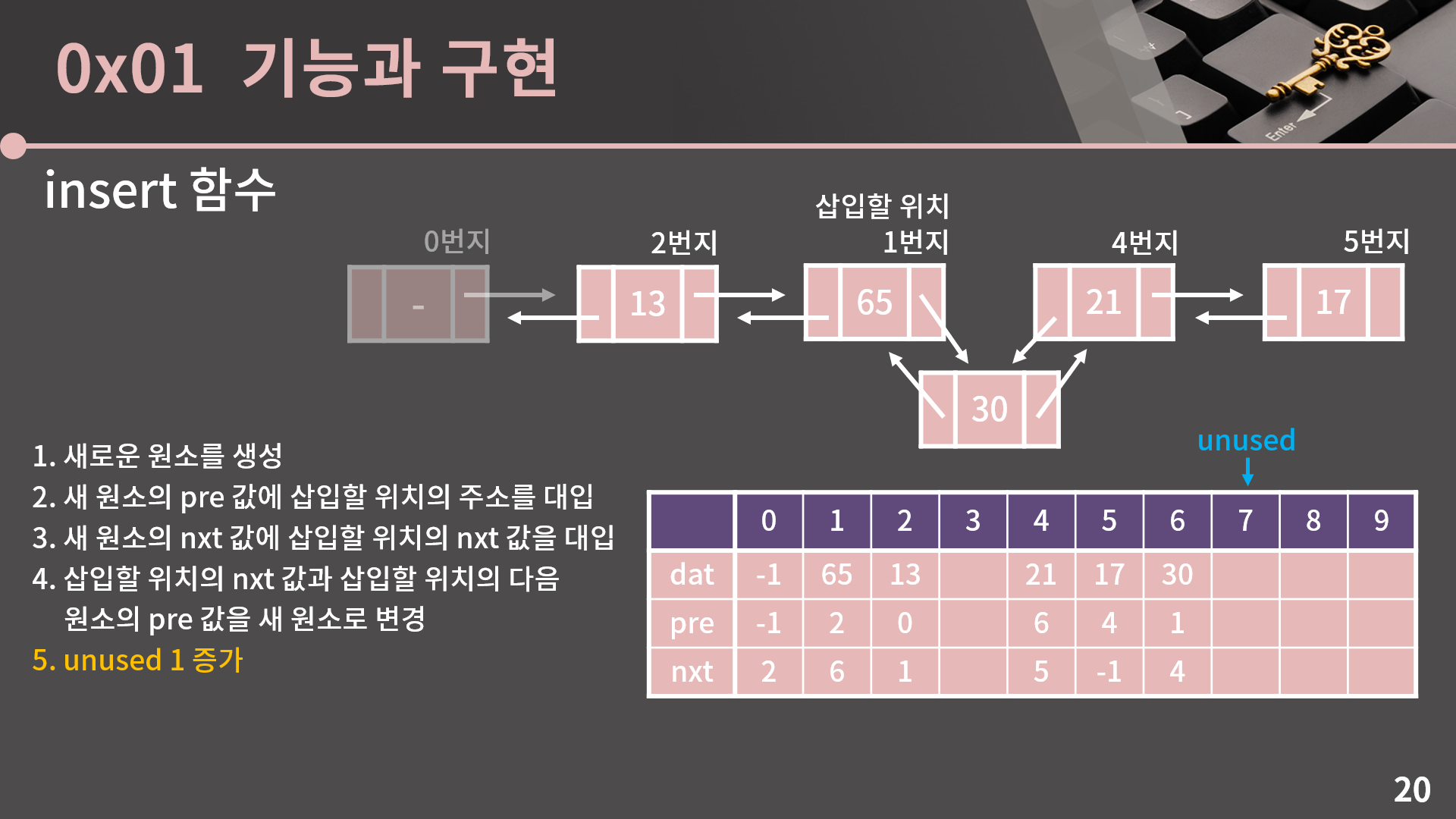
마지막으로 한 단계가 더 남았는데, 이제 unused 칸을 다 썼으니 unused를 1 증가 시켜서 다음 insert에는 비어있는 7번지를 쓸 수 있게끔 해야 합니다.
이제 이 과정을 따라서 구현을 하면 됩니다. 먼저 시도를 해보도록 합시다. insert 함수를 다 채운 후에 insert_test() 함수를 실행했을 때의 결과가 주석으로 달아놓은 모양과 동일한지를 확인해보면 됩니다. 다 짜신 후에 제 코드를 확인해보세요.

코드의 내용이 각 단계에 딱 대응이 되기 때문에 읽을 때 크게 어려울 건 없을 것입니다. 주의해야할건 05번째 줄에서 if(nxt[addr] != -1)이라는 처리가 들어간건데, 맨 마지막 원소의 뒤에 새 원소를 추가하는 상황이라면 "삽입할 위치의 다음 원소"가 존재하지 않습니다. 그런데도 pre[nxt[addr]] = unused; 로 써버리면 pre[-1]에 접근할 수 있습니다. 그래서 nxt[addr]가 -1이 아닐 때에만 pre[nxt[addr]]에 unused를 대입하도록 했습니다.
코드가 헷갈리면 이전 슬라이드들에서 하던 것 처럼 직접 표를 그려놓고 한 줄씩 손으로 값의 변화를 따라가보면 도움이 될 것입니다.

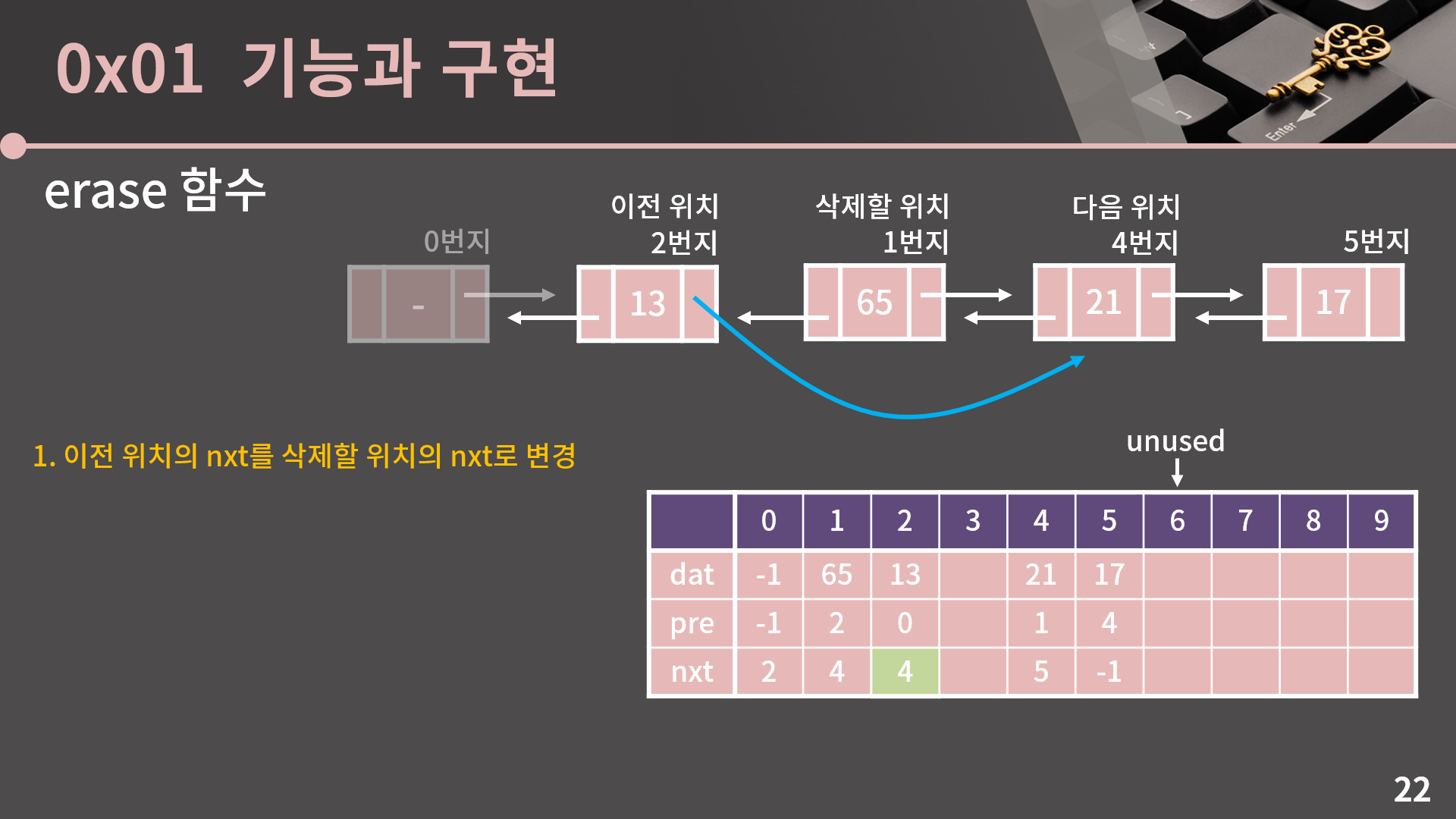
다음으로 erase 함수를 설명드리겠습니다. 그 전에 insert 함수를 익힌 것을 바탕으로 erase 함수는 직접 짜보겠다! 뭐 이런 자세 정말 좋습니다. 한 번 시도해보면 좋습니다.
설명을 이어가겠습니다. 설명의 편의를 위해 65를 지우고 싶다고 할 때, 65를 삭제할 위치, 앞의 원소(=13)를 이전 위치, 뒤의 원소(=21)를 다음 위치라고 부르겠습니다. 보면 erase는 insert보다 과정이 훨씬 짧습니다. 첫 번째로 이전 위치의 nxt를 삭제할 위치의 nxt로 변경합니다.

두 번째로 다음 위치의 pre를 삭제할 위치의 pre로 변경합니다. 이 두 과정만 하면 삭제가 끝이 납니다. 지금 보면 정작 삭제할 위치인 1번지에서는 dat, pre, nxt는 전혀 건드리지 않는 것을 볼 수 있는데, 앞으로 이 값들은 아무 의미가 없습니다. 제거된 원소고, 앞으로 그 어떤 nxt나 pre도 1번지를 가리키지 않을 것이기 때문입니다.
이런 상황이니까 굳이 dat, nxt, pre 값을 -1과 같은 다른 값으로 덮을 필요가 없고 그냥 내버려두면 됩니다. 대신 이러한 구현 방법 때문에 이 야매 연결 리스트에서는 제거된 원소가 프로그램이 종료될 때 까지 메모리를 점유하고 있게 되고, 그렇기에 실무에서는 사용할 수 없는 구현 방식입니다.
하지만 알고리즘 문제에서는 insert의 횟수가 10만 번 혹은 100만 번과 같이 제한이 있기 마련이고, 그럴 때에는 그냥 배열을 그 제한에 넉넉하게 잡아버리고 나서 이 야매 연결 리스트를 사용하면 됩니다.
구현도 곧이 곧대로 하면 됩니다. 작성하고 erase_test() 함수로 테스트도 해보세요.

이제 제 코드를 확인해보세요. 크게 어렵지는 않을 것 같은데, insert 함수때와 비슷하게 if(nxt[addr] != -1)이라는 처리가 되어있는 것을 볼 수 있습니다.
왜 pre[addr]이 -1인지는 체크를 하지 않아도 되는데 nxt[addr]이 -1인지는 체크를 해야 하는지 한 번 고민하는 시간을 가져봐도 괜찮을 것 같습니다.
그 이유는 dummy node의 존재로 인해 그 어떤 원소를 지우더라도 pre[addr]은 -1이 아님이 보장되지만 nxt[addr]는 제일 마지막 원소를 지우는 상황에서 값이 -1일 수 있기 때문에 그렇습니다.
insert, erase를 메꾼 전체 코드는 github에서 확인할 수 있습니다. 지금 제 구현체에서는 제일 마지막 원소를 O(N)에 확인할 수 있는데, 조금만 바꾸면 제일 마지막 원소도 O(1)에 확인할 수 있게 만들 수 있습니다. 하지만 이 부분은 여러분에게 맡기겠습니다.

우리의 기대를 저버리지 않고 STL에는 list가 있습니다. STL을 사용할 수 있는 상황이라면 연결 리스트를 꾸역꾸역 구현하는 것 보다 그냥 STL을 쓰는게 훨씬 더 편하니 STL list의 사용법을 익혀두면 좋습니다. vector 때처럼 예시를 가지고 같이 이해해보겠습니다.
일단 STL list에서 push_back, pop_back, push_front, pop_front는 모두 O(1)이고, 우리가 이전 구현에서 '번지'라는 개념을 사용했듯 여기서는 iterator가 주소 역할을 합니다. 03번째 줄에서 list::iterator라는 type을 치기가 귀찮으면 C++11 이상일 때 auto t = L.begin()으로 써도 됩니다.
그리고 erase는 제거한 다음 원소의 위치를 반환합니다. 마지막으로 순회를 할 때에는 C++11 이상이라면 12번째 줄과 같이 편하게 할 수 있지만, C++11 미만이라면 14, 15번째 줄과 같이 아주 불편하게 할 수 밖에 없습니다.
야매 연결 리스트에서는 0번지, 즉 제일 앞의 원소를 더미 노드로 사용하지만 STL list에서는 제일 뒤의 원소가 더미 노드입니다. 그래서 L.begin()은 제일 앞에 있는 원소를 가리키지만 L.end()는 제일 뒤에 있는 원소의 한 칸 뒤를 가리킨다는 점에 주의하셔야 합니다.

이제 연습문제를 풀어보겠습니다. BOJ 1406번: 에디터 문제를 사이트에 들어가서 확인해주세요. 연결 리스트가 쓰이는 문제는 크게 응용해서 낼만한게 없고 지금 문제와 같이 원소들을 돌아다니면서 이동하다가 삭제나 삽입이 필요한 문제들입니다. 그런데 만약 N이 5000 정도로 작다면 그냥 O(N2)으로 짜도 통과되니 아무래도 우리에게 더 익숙한 vector로 구현을 하면 됩니다. 하지만 지금은 N이 굉장히 커서 연결 리스트를 이용해 구현을 해야 하는데 조금 감이 안올 수도 있을 것 같아 그림으로 느낌을 좀 잡아드리겠습니다.
첫 번째 예제를 보면 주어진 문자열이 abcd이니까 연결 리스트를 일단 만들겠습니다. 그리고 커서는 문장의 맨 뒤에 위치하고 있다고 했는데, 엄밀히 말하면 커서는 글자와 글자 사이에 있어야 하지만 구현의 편의를 위해 커서가 글자를 가리킨다고 생각을 하겠습니다. 그래서 커서가 d를 가리키고 있다고 하겠습니다.
첫 번째 명령은 x를 추가하라는 명령이니 d 뒤에 x를 추가하면 됩니다. 그리고 잘 생각해보면 커서도 오른쪽으로 옮겨가야 합니다. 왜냐하면 입력을 하면 당연히 커서가 한 칸 오른쪽으로 이동하기 때문입니다.
L, D 명령은 말그대로 커서를 왼쪽이나 오른쪽으로 옮기면 되는거고 B 명령도 연결 리스트에서 커서가 가리키는 원소를 지우는 명령인걸 알 수 있습니다. 이제 연결 리스트로 구현을 하는 일만 남았습니다.
이 그림과 설명은 야매 연결 리스트에서의 상황을 나타냅니다. 야매 연결 리스트에서는 더미 노드가 제일 앞에 위치하기 때문에 "abcd"에서 실제 커서가 제일 앞에 위치할 경우 연결 리스트에서는 더미 노드를 가리키고 있고, 제일 뒤에 위치할 경우 연결 리스트에서는 d를 가리키고 있습니다. 하지만 STL list에서는 더미 노드가 제일 뒤에 위치하기 때문에 실제 커서가 제일 앞에 위치할 경우 연결 리스트에서는 a를 가리키고 있고, 제일 뒤에 위치할 경우 d의 한 칸 뒤인 L.end()를 가리키고 있습니다. 실제 커서가 있는 위치에 따라 연결 리스트에서 커서가 어디를 가리켜야 하는지 잘 생각해서 구현을 해보세요.
STL list와 야매 연결 리스트 둘 다를 이용해서 풀어보는 것을 추천드립니다. 아직 사용법이 낯설어서 조금 어려울 수 있지만 못할 정도의 난이도는 아니니까 화이팅입니다.
(다음 슬라이드에 바로 코드가 나옵니다.)

첫 번째로는 STL list를 이용한 코드를 소개해드리겠습니다. 달리 설명할건 없고, 그냥 문제에서 요구한대로 커서를 이동시키다가 삽입과 삭제를 했습니다. cursor가 L.begin()인데 명령 L이 들어온다거나, L.end()인데 D가 들어온다거나 했을 때에 대한 예외처리를 23, 26번째 줄처럼 해두어야 합니다.
이외에 또 짚고가면 좋을 점들은 명령과 글자가 다 char 1글자여서 char 자료형에 cin을 받도록 했고, 이렇게 하면 알아서 공백과 줄바꿈은 무시합니다.
혹시 다른 문제에서라도 getline과 같은 함수를 이용할 때 쓸데없이 줄바꿈이 끼어 들어가서 골치아플 수 있는데, 그럴 땐 그냥 임시 변수에 getline으로 한 번 줄바꿈을 걸러내던가 하는 방식으로 구현을 하면 됩니다.
직접 구현을 하다보면 런타임 에러를 수도 없이 많이 받을 것 같은데, 워낙 코드가 가양각색이라 직접 오랜 시간을 들여 분석을 해봐야 이유를 알 수 있을테지만 대부분의 경우에는 이미 cursor가 가리키는 곳이 이미 지워졌는데 그 곳에 insert를 시킨다거나, cursor가 L.begin()인데 cursor--;를 시킨다거나 하는 이유일 것입니다.
직접 짰는데 계속 틀릴 때 정말 화가 나고 포기하고 싶겠지만 코딩테스트를 잘 넘기려면 언젠가는 거쳐가야하는 과정이니 제 코드에만 의존하지말고 중간중간 출력을 찍어보며 어디가 잘못되었는지 찾아내고, 코드를 고쳐서 꼭 스스로의 힘으로 올바른 코드를 만들어봤으면 좋겠습니다. (코드 링크)

두 번째 코드는 저희가 열심히 짰던 야매 연결 리스트를 이용한 방법입니다. 진짜 억지로 어찌저찌 한 페이지에 다 몰아서 뒀는데, 아무튼 STL list를 쓸 땐 커서가 list::iterator에 대응됐고 여기서는 주소에 대응됩니다. 이후에는 상황에 맞게 구현을 하면 됩니다. (링크)

그 다음 문제는 별다른건 아니고 면접이나 손코딩에서 물어볼만한 문제 3가지를 알려드리겠습니다. 정답을 고민해보세요.
첫 번째 문제는 다음과 같습니다. 효율적으로 구하라는 의미는 생각한 풀이의 공간복잡도와 시간복잡도를 생각해보라는 의미입니다.

이 문제의 정답은 별다른게 아니고 그냥 시작점을 어디 따로 저장해뒀다가 동일한 노드가 나올 때 까지 계속 다음 노드로 가는 방식입니다. 공간복잡도는 O(1)이고 시간복잡도는 O(N)입니다.

두 번째 문제를 풀어볼겠습니다. 참고로 이 문제는 제 고등학교 자료구조 및 알고리즘 과목에서 기말고사 문제였습니다. 아직까지도 기억이 나네요.
풀이를 떠올리셨나요? 이왕이면 공간복잡도를 O(1)로 해결하는 방식을 고민해봅시다.

정답은 다음과 같습니다. 지나가면서 스치는 모든 노드를 저장하지 말고, 먼저 둘의 길이 차이를 구한 다음에 더 긴 쪽을 차이만큼 이동시켜놓으면 이제는 둘을 동시에 한 칸씩 당겼을 때 만나는 지점을 구할 수 있게 될 것입니다.

세 번째 문제를 풀어볼게요. 화이팅! 아마 공간복잡도가 O(N)인 방법이 직관적으로 생각이 나실테지만 공간복잡도가 O(1)인 방법이 존재합니다. 이 방법을 찾아보려고 노력해보면 좋겠습니다.

이 문제는 Floyd's cycle-finding algorithm이라는 이름이 붙어있는 알고리즘으로 해결이 가능한데, 한 칸씩 가는 커서와 두 칸씩 가는 커서를 동일한 시작점에서 출발시키면 사이클이 있을 경우 두 커서는 반드시 만나게 됩니다. 반대로 만약 사이클이 없으면 두 커서가 만나지 못하고 연결 리스트의 끝에 도달합니다.
이 방식을 이용하면 거치는 모든 노드를 저장할 필요가 없이 공간복잡도 O(1)에 사이클의 존재 여부를 알 수 있습니다.
사실 문제 2, 3번 정도면 꽤나 어려운 편이기 때문에 모른다고 해서 큰 일이 있는건 아니지만 혹시 면접에서 얻어걸리면 본인의 능지를 뽐낼 수 있으니까 너무 부담가지지는 마시고 가볍게 음미하고 넘어가겠습니다.

고생 많으셨습니다. 연결 리스트가 무엇인지는 크게 어렵지 않게 익혔을텐데 구현에서 애를 많이 먹었을 것 같습니다. 연결 리스트가 코딩테스트에 썩 자주 나오는 유형은 아니지만 그래도 안 하고 넘어가기는 그런 자료구조라 이렇게 다루게 되었습니다. 개인적으로는 이번 강의에서 애니메이션을 만드는게 정말 힘들었습니다ㅠㅠ 시간을 많이 쏟은 만큼 보시는 여러분들이 이해가 잘 가면 좋겠고, 잘 이해가 안가는 부분이 있다면 편하게 댓글 남겨주세요.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x07강 - 덱 (39) | 2020.03.14 |
|---|---|
| [실전 알고리즘] 0x06강 - 큐 (14) | 2020.03.11 |
| [실전 알고리즘] 0x05강 - 스택 (47) | 2020.03.08 |
| [실전 알고리즘] 0x03강 - 배열 (61) | 2020.02.26 |
| [실전 알고리즘] 0x02강 - 기초 코드 작성 요령 II (53) | 2020.02.16 |
| [실전 알고리즘] 0x01강 - 기초 코드 작성 요령 I (80) | 2020.02.12 |