
안녕하세요, 이번 시간에는 다이나믹 프로그래밍을 다룹니다. 직전까지 막 재귀, 백트래킹, 정렬 이런 것들로 되게 고통받으셨을텐데 오늘껀 개념도 그렇게 어렵지 않고 구현 난이도도 낮아서 많이 수월합니다.

다이나믹 프로그래밍은 개념을 크게 설명할게 없고 그냥 정말 다양한 문제를 풀어보면서 익히면 됩니다. 그래서 이번 강의에서는 문제를 주구장창 같이 풉니다.

일단 다이나믹 프로그래밍을 알파벳 앞 글자만 따서 DP라고 부르기도 합니다. 강의 내에서도 DP라고 계속 부르겠습니다. DP는 저기 써져있는 것 처럼 여러 개의 하위 문제를 먼저 푼 후에 그 결과를 쌓아올려서 주어진 문제를 해결하는 알고리즘입니다. 원래 정의란게 늘 그렇듯 저 표현으로는 잘 이해가 가지 않습니다. 쉽게 설명하면 문제를 해결하기 위한 점화식을 찾아낸 후 점화식의 항을 밑에서부터 차례로 구해나가서 답을 알아내는 형태의 알고리즘을 말합니다.
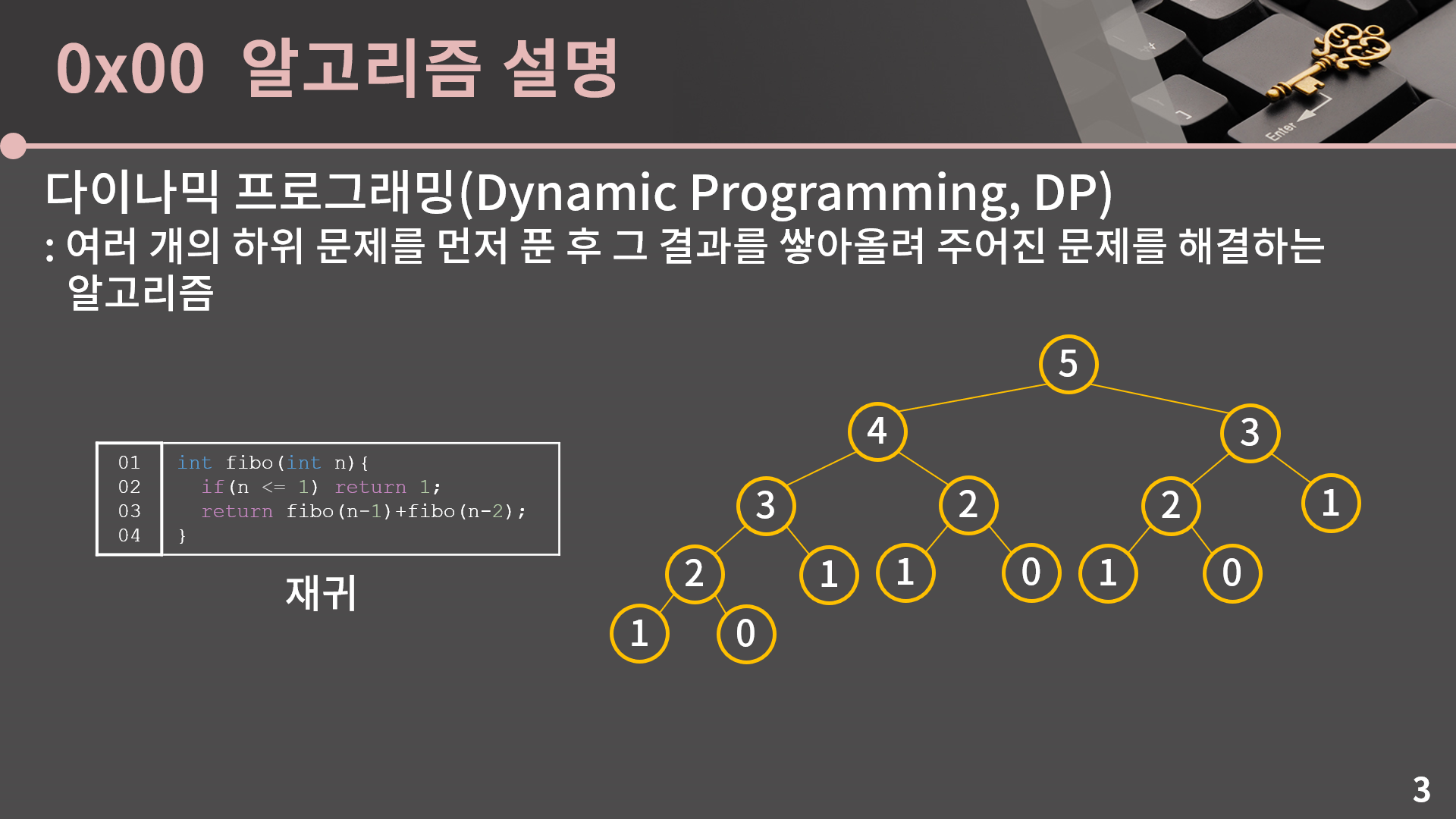
가장 쉬운 예시로 피보나치 문제를 소개할 수 있습니다. 0x0B강 재귀 단원에서 스쳐가듯 설명을 했었지만, 피보나치 수열의 N번째 항을 지금처럼 재귀적으로 구하면 중복된 연산이 계속 발생해서 O(1.618N)의 시간이 걸립니다.

그런데 피보나치 문제를 DP로 해결하면 이렇게 미리 배열을 만들어두고 0번째 인덱스부터 하나씩 채워가는 방식으로 해결할 수 있고 N+1칸을 채우고 나면 답을 알 수 있으니 O(N)에 답을 알아낼 수 있습니다. 이렇게 중간 결과를 저장해서 이용하는지 그렇지 않은지에 따라 극적인 시간복잡도의 차이가 발생합니다.

DP를 풀기 위해서는 먼저 테이블을 정의해야 하고 점화식을 찾은 후에 초기 값을 정해야 합니다. DP는 작정하고 어렵게 하고자 한다면 한도 끝도 없이 어려워지지만 코딩테스트에 나올 수준의 DP 문제는 일단 점화식만 찾고나면 그 뒤는 초기 값을 채워넣은 후에 반복문을 돌면서 배열을 채우면 끝이어서 구현이 굉장히 쉽습니다.
하지만 다양한 DP 문제를 풀어봤거나 뛰어난 수학적 직관력을 가지고 있지 않은 이상 문제에서 점화식을 이끌어내는 과정이 그렇게 쉽지 않고, 무엇보다도 초보 단계에서는 주어진 문제가 DP로 푸는 문제라는 것 자체를 알아차리지 못할 수도 있습니다. 그래서 이번 강의에서는 쉬운 문제를 많이 다뤄서 테이블을 잡고 식을 찾는 연습을 같이 해보려고 합니다. 여러분들도 그룹 내의 문제집에 올려둔 적당한 난이도의 DP 문제들을 많이 풀고 식을 머릿속으로 고민하면서 많은 유형을 학습하고 숙달하는게 중요합니다. 그래야 코딩테스트에서 DP 문제가 나왔을 때 빠르게 쓱싹할 수 있습니다.
바로 시작해보겠습니다. BOJ 1463번: 1로 만들기 문제를 보겠습니다. 일단 이 문제를 딱 보면 DP 말고 지금까지 우리가 배운 알고리즘 중 하나로 문제를 풀 수 있다는 생각이 바로 들었다면 스스로의 발전에 대해 아주 만족을 하셔도 좋을 것 같습니다. 이 문제는 바로 BFS를 가지고 해결이 가능합니다. dist 배열을 하나 만들어두고 1을 초기값으로 한 뒤 x2, x3, +1으로 뻗어나가면 됩니다. 그런데 DP를 이용하면 훨씬 짤막하게 구현에 성공할 수 있습니다.

먼저 테이블은 위와 같이 정의하겠습니다. 문제를 보고 테이블을 어떻게 정의할지는 특별한 공식이나 방법론이 있는게 아니라 그냥 경험적으로 익히게 됩니다. 문제를 많이 풀다보면 자연스럽게 새로운 문제를 봐도 테이블을 어떤 식으로 잡으면 되겠다 하는 느낌이 오게 됩니다. 아무튼 테이블을 이렇게 정의한 상황에서 테이블의 값들을 어떻게 채우면 좋을지 고민하겠습니다.
구체적인 예시를 들어서 설명해보면 D[12]를 어떻게 구할 수 있을지 생각해봅시다. D[12]의 값을 직접 구하라는 의미가 아니라 식을 생각해보자는 의미입니다. 더 구체적으로 말을 하면 지금 D[1]부터 D[11]까지의 값을 다 알고 있다고 하겠습니다. 그러니까 1, 2, 3, ..., 11을 1로 만들기 위한 최소 횟수를 다 알고 있다고 하면 이런 상황에서 D[12]를 구하는 방법은 12에서 할 수 있는 연산을 생각해보면 됩니다.

12에서 할 수 있는 연산은 3가지가 있는데 3으로 나누거나 2로 나누거나 1을 빼거나입니다. 그리고 이 연산들로부터 식이 유도됩니다. 12를 3으로 나누면 4가 될거고, 4에서 1로 가는건 이미 D[4]에 있으니 바로 가지고 오면 됩니다. 2로 나누거나 1을 빼는 상황도 마찬가지입니다. 그래서 최종적으로 D[12] = min(D[4] + 1, D[6] + 1, D[11] + 1)이라는 식을 얻을 수 있습니다.

비슷한 방법으로 생각해보면 D[k]를 구하고 싶을 때 3으로 나누어지면 3으로 나눠서 D[k] = D[k/3] + 1을 얻어내고, 2로 나누어지면 2로 나눠서 D[k] = D[k/2] + 1을 얻어내고, 1은 언제나 뺄 수 있으니 D[k] = D[k-1] + 1을 얻어서 이들 중에서 최솟값을 택하면 됩니다.
마지막으로 초기값을 생각해봐야 하는데, 마치 피보나치 수열에서 초항과 두 번째 항이 1, 1인 것 처럼 점화식에는 당연히 초기값이 있어야 합니다. 이 문제에서는 D[1] = 0을 초기값으로 주면 나머지는 점화식을 가지고 값을 계산할 수 있습니다. 매번 점화식이 돌아갈 수 있게 하기 위한 초기값이 어디까지인지를 고민해서 초기값을 잘 적용해야 하는데 이 문제에서는 D[1]만 정해주면 됩니다.
다음 장에는 바로 코드가 나오니 바로 구현을 시도해봅시다. D 테이블을 하나 전역에 잡고 for문을 돌면서 테이블을 채우면 끝입니다.

여러분들도 느끼셨을지 모르겠지만 이 자료를 만드는 저도 지금 이 장을 만들면서 신기했던게 진짜 오랜만에 코드가 한 장에 다 담깁니다. 이렇게 DP는 구현이 굉장히 짤막한 편입니다.(코드 링크)
코드를 보면 일단 d[1] = 0 초기값을 줍니다. 사실 d를 전역에 선언해서 다 0으로 초기화가 되어있으니 이 명령이 없어도 되긴 하지만 보는 사람의 편의를 위해 한 줄 끼워놨습니다. 그리고 i = 2부터 n까지 for문을 돌면서 d[i]를 앞에서 본 것 처럼 d[i-1]+1, d[i/2]+1, d[i/3]+1을 가지고 갱신하면 끝입니다. 이렇게 첫 번째 DP 문제를 가뿐하게 넘어가겠습니다.
두 번째 문제는 BOJ 9095번: 1, 2, 3 더하기 문제입니다. 일단 사실 이 문제 자체는 N이 워낙에 작은지라 DP를 안쓰고 10중 for문이나 백트래킹 같은걸 써서도 해결이 가능하지만 N이 커지면 DP가 아닌 다른 방법은 쓸 수가 없습니다. 그래서 DP로 문제를 풀이해보겠습니다.

제일 먼저 테이블을 정의해보면 앞 문제에서의 상황을 생각했을 때 딱 떠오르는 형태가 있습니다. 바로 D[i] = i를 1, 2, 3의 합으로 나타내는 방법의 수라고 정의하는 방법입니다. 이걸 바탕으로 점화식을 만들어야 할텐데 어떻게 예쁜 점화식을 만들 수 있을지 같이 고민해보겠습니다. 바로 점화식을 보여드려도 되지만 같이 생각하는 시간을 가져본다는 차원에서 D[4]를 같이 구해보겠습니다.

4를 1, 2, 3의 합으로 나타내는 방법들은 본문에도 있지만 이렇게 7가지가 있습니다. 그러면 D[4] = 7이란걸 바로 알 수가 있는데 저희는 지금 단순히 값을 구하자는게 목표가 아니라 관계식을 이끌어내자는게 목표여서 관점을 조금 달리해서 볼 필요가 있습니다. 힌트를 드리자면 제가 괜히 이렇게 세 줄에 7가지를 나눠서 쓴게 아닌데 각 줄의 공통점이 보이시나요?

이렇게 첫 번째 줄은 제일 끝의 값이 1이고, 두 번째 줄은 2, 세 번째 줄은 3입니다. 먼저 끝의 값이 1인 경우들을 생각할 때 끝의 값이 1로 정해지면 결국 3을 1, 2, 3의 합으로 만드는 방법들을 나열한 후 끝에 1을 붙이는 상황입니다. 즉 끝의 값이 1인 경우가 4개인 이유는 D[3]이 4이기 때문입니다.
끝의 값이 2일 땐 2를 1, 2, 3의 합으로 만드는 방법들을 나열한 후 끝에 2를 붙이는 상황이니 D[2]의 값을 가져오면 되고 끝의 값이 3일 땐 1을 1, 2, 3의 합으로 만드는 방법들을 나열한 후 끝에 3을 붙이는 상황이니 D[1]의 값을 가져오면 됩니다. 종합했을 때 D[4]는 D[1] + D[2] + D[3]이라는 것을 알 수 있습니다. 이렇게 i를 1, 2, 3의 합으로 나타내는 방법의 수를 구하기 위해 가장 끝에 오는 수가 1인 경우, 2인 경우, 3인 경우로 나눠서 생각해보면 각각은 D[i-1], D[i-2], D[i-3] 가지이기 때문에 D[i] = D[i-1] + D[i-2] + D[i-3]임을 알 수 있습니다.

초기값을 생각해보면 D[1]과 D[2]와 D[3]이 주어져야 합니다. 식이 D[i] = D[i-1] + D[i-2] + D[i-3]이니 자연스럽게 초기값이 최소 3개는 주어져야 한다는걸 알 수 있습니다. 테이블을 정의했고 점화식을 찾았고 초기값도 정했으니 바로 구현을 해보겠습니다.
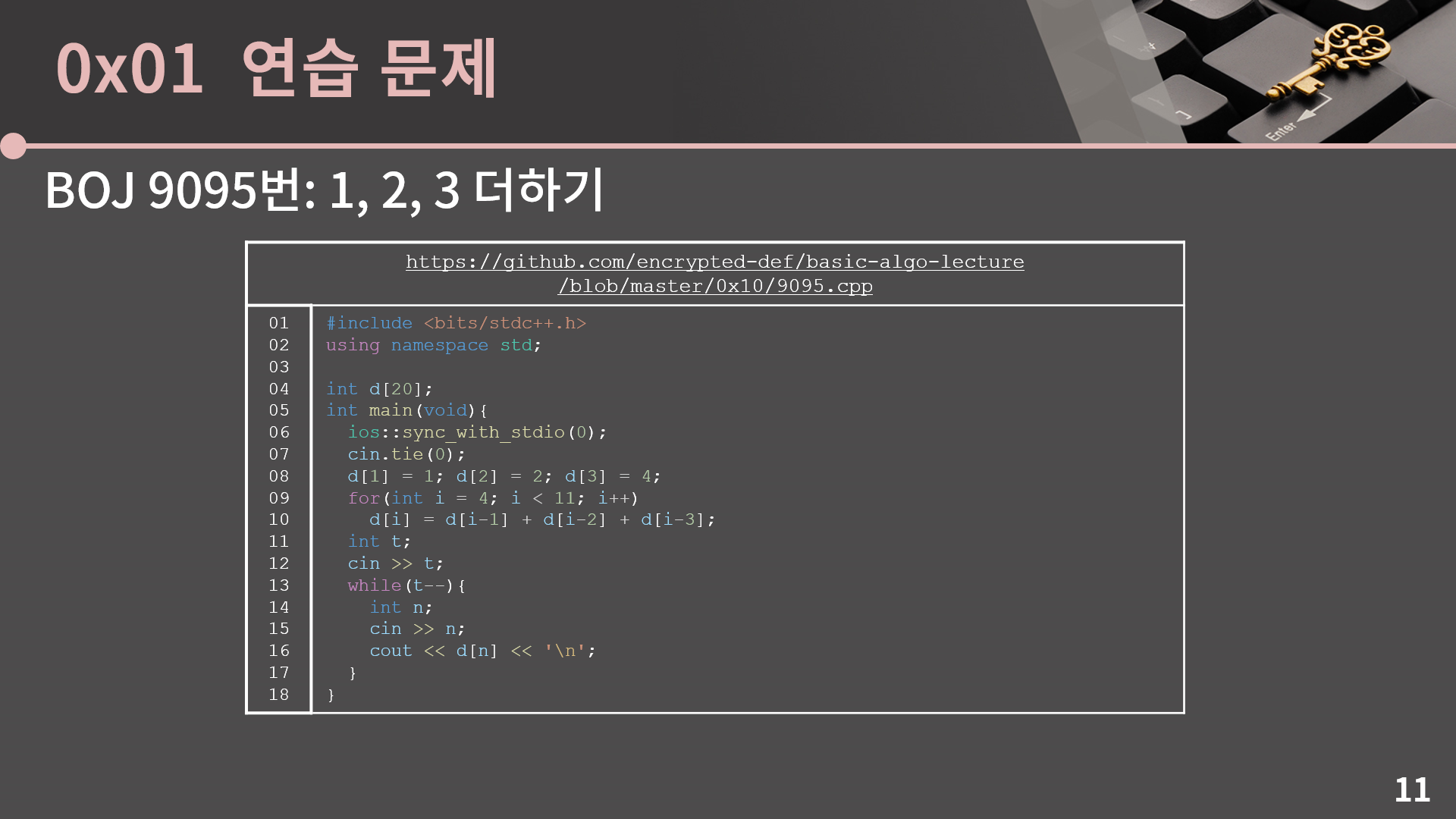
바로 코드를 보여드리면 이렇게 간단하게 짤 수 있습니다. 테이블을 바깥에서 미리 다 계산해둔 후에 매번 n이 들어올 때 마다 d[n]을 바로 출력해줬습니다. 이 문제에서야 워낙 n이 작으니 상관은 없다만 다른 문제를 풀다가 비슷한 상황이 또 있다면 n이 주어질 때 마다 매번 d[1]부터 d[n]까지 새로 구하는 것 보다 미리 다 구해두는게 효율적이란걸 기억합시다.
그리고 테이블에 값을 어디까지 넣어두고 어디서부터는 for문으로 돌려서 값을 넣을지도 잘 생각해볼 문제입니다. 저는 d[1], d[2], d[3]까지는 초기값으로 주고 d[4]부터는 알아낸 식을 가지고 계산했습니다.(코드 링크)
세 번째 문제는 BOJ 2579번: 계단 오르기 문제입니다. 문제가 정보올림피아드 초등부 기출문제라는 점에서 요새 초등학생들은 저런걸 푸나 살짝 기분이 쎄하지만 아무튼 풀이를 같이 해보도록 하겠습니다.
만약 N이 한 20 정도로 그다지 크지 않았다면 백트래킹과 같은 방법을 통해 대략 O(2N)으로 해결이 가능하지만 지금처럼 N이 300일 땐 어림도 없습니다. 뭐 예상하다시피 이 문제는 DP로 해결이 가능합니다.

지금까지 해왔던 것 처럼 테이블을 정의해야 하는데 그냥 쉽게 생각나는 대로 D[i] = i번째 계단까지 올라섰을 때 점수 합의 최댓값이라고 두겠습니다. 이 다음으로 점화식을 찾아야하는데 사실 그게 잘 안됩니다. 일단 직접 손으로 구해보면 이렇게 D[1] = 10, D[2] = 30, D[3] = 35인걸 알 수 있는데, D[i]의 값을 가지고는 점화식을 세우고 싶어도 연속한 세 계단을 모두 밟아서는 안 된다는 제약 조건을 점화식에 넣을 방법이 없습니다. 그래서 슬프지만 지금의 D[i]는 문제를 풀기에 적절하지 않습니다.

그러면 다른 테이블 정의를 찾아야 하는데, D[i][j] = 현재까지 j개의 계단을 연속해서 밟고 i번째 계단까지 올라섰을 때 점수 합의 최댓값, 단 i번째 계단은 반드시 밟아야 함 으로 정의하겠습니다. 왜 이렇게 2차원이 된거냐면, 지금까지 몇 개의 계단을 밟았는지에 대한 정보가 추가로 있어야 점화식을 세울 때 계단을 오르는 규칙을 고려할 수 있기 때문입니다. 그리고 나중에 보면 알겠지만 단 i번째 계단은 반드시 밟아야 함 이라는 조건이 있어야 점화식을 이끌어낼 수 있습니다. 역시 이런건 짬에서 나오는 바이브라 보면서 잘 익혀가셔야 합니다.
이 2차원 배열에서 j는 어떤 값을 가지냐 보면 i번째 계단을 반드시 밟아야 한다는 조건이 있어서 j = 1 혹은 2입니다. 연속된 세 개의 계단을 모두 밟아서는 안된다는 조건으로 인해 j가 3 이상일 수는 없습니다. 그러면 이제 우리는 D[i][1]과 D[i][2]를 채워야하는데 점화식을 고민해보겠습니다.

이전 문제들에서는 D[12]나 D[4]와 같이 직접적인 값을 가지고 얘기를 했는데 두 문제를 통해 어느 정도 테이블을 채워나간다는 것에 대한 감이 생겼을 것 같아서 이제는 조금 추상화를 해서 직접적인 값이 아니라 D[k][1]을 채운다고 생각을 하겠습니다.
먼저 D[k][1]이 의미하는 값이 무엇인지 테이블의 정의를 그대로 가져오겠습니다. 그러면 D[k][1]는 현재까지 1개의 계단을 연속해서 밟고 k번째 계단까지 올라섰을 때 점수 합의 최댓값입니다. 현재까지 1개의 계단을 연속해서 밟았다는 의미는 곧 k-1번째 계단을 밟지 않았다는 의미입니다. 그러면 계단을 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다고 했으니 k-2번째 계단을 밟았다는건 너무나 자명합니다. 우린 어디까지나 점화식만 이끌어내는게 목표여서 k-2번째 밑으로 내려갈 필요가 없습니다. k-2번째 계단을 밟았을 때 얻은 점수의 최댓값은 D[k-2][1] 혹은 D[k-2][2]에 잘 저장되어 있으니 최종적으로 D[k][1] = max(D[k-2][1], D[k-2][2]) + S[k]임을 알 수 있습니다. (S[k]는 k번째 계단에 쓰여 있는 점수를 의미합니다.)
그 다음으로는 D[k][2]인데, D[k][2]는 현재까지 2개의 계단을 연속해서 밟고 k번째 계단까지 올라섰을 때 점수 합의 최댓값입니다. 현재까지 2개의 계단을 연속해서 밟았다고 했으니 k-1번째 계단을 밟았다는건 알 수 있는데, 추가적인 조건 1개가 더 있습니다. k-1번째 계단을 밟을 당시에는 1개의 계단을 연속해서 밟은 상태여야 합니다. 만약 k-1번째 계단을 밟을 당시에 2개의 계단을 연속해서 밟은 상태였다면 연속한 세 개의 계단을 모두 밟아서는 안 된다는 조건으로 인해 k번째 계단을 밟는게 불가능하기 때문입니다. 그렇기 때문에 D[k][2] = D[k-1][1] + S[k]가 됩니다.
이렇게 얻어낸 식을 가지고 테이블을 채운 뒤에 마지막 도착 계단은 반드시 밟아야 한다는 조건을 고려해 max(D[N][1], D[N][2])를 출력하면 끝입니다.

초기값을 어디까지 둬야하는지 생각해보면 아까 앞에서 식에서 봤듯 D[k][1]을 구할 때 D[k-2][1], D[k-2][2] 테이블을 참고했습니다. 그러면 D[1][1], D[1][2], D[2][1], D[2][2]을 다 초기값으로 주는게 바람직합니다. D[1][1]과 D[1][2]은 주는게 너무나도 당연하고 D[2][1]의 경우도 초기값을 안주고 점화식으로 계산을 하려고 하면 D[0][1], D[0][2] 값을 가져와야 하는게 좀 이상하기 때문입니다. D[2][2]는 엄밀히 말하면 초기값으로 안주고 계산을 해도 되긴 하는데 그냥 D[2][2]도 초기값으로 주면 코드가 좀 더 깔끔해져서 그렇게 했습니다.

코드는 이렇게 생겼고 특별하게 설명할건 없습니다. 다만 n이 1일 때 예외처리를 왜 했는지 생각해보면 좋겠는데, n = 1일 때 d[2][1], d[2][2], s[2] 이런 값에 접근하는게 바람직하지 않기 때문입니다. 그래서 n = 1일 때에는 바로 s[1]을 출력한 후 프로그램을 종료하도록 했습니다. 그리고 설명의 편의를 위해 인덱스를 모두 1-indexed로 두었지만 0-indexed로 둬도 상관없습니다. 0-indexed로 두면 공간을 조금 더 적게 사용한다는 장점이 있긴 한데 그래봤자 쥐꼬리만한 차이여서 1-indexed로 할지 0-indexed로 할지는 자기가 이해하기 쉬운대로 하면 됩니다.(코드 링크)
이렇게 문제를 풀고 끝인가 싶겠지만 아직 할 얘기가 더 남아있습니다. 이 문제에서 관점을 살짝 바꿔서 보면 2차원 배열 대신 1차원 배열로 문제를 해결할 수 있습니다. DP를 연습하는 차원에서 풀이 방향과 테이블의 정의만 알려드릴테니 이번에는 여러분이 직접 점화식을 세우고 초기값을 정해보는 시간을 가져보겠습니다.

관점을 어떻게 바꿔볼거냐면 아까와는 다르게 이번에는 밟지 않을 계단을 선택할 예정입니다. N번째 계단까지 점수의 최댓값을 구하는 상황은 곧 밟지 않을 계단의 합을 최소로 만드는 상황과 똑같기 때문입니다. 그리고 저는 D[i]를 i번째 계단까지 올라섰을 때 밟지 않을 계단의 합의 최솟값, 단 i번째 계단은 반드시 밟지 않을 계단으로 선택해야 함으로 정의했습니다. 이제 여러분들이 점화식을 세워보셨으면 좋겠는데 계단을 오르는 규칙을 비틀어서 생각해보면 우리는 k번째 계단을 밟지 않았으면 k-1번째 계단은 무조건 밟아야하고, 또 k-2번째 계단이나 k-3번째 계단 중에서 하나는 무조건 밟는 계단으로 선택해야 한다는걸 알 수 있습니다. 잠깐 멈춰놓고 이 성질을 바탕으로 식을 찾아보도록 합시다.
아마 제 생각에 식을 찾아내신 분이 그렇게 많을 것 같지는 않습니다. 뭐 당연합니다. 지금 고작 3문제 같이했다고 몇십분만에 갑자기 막 DP에 눈이 뜨이고 그런건 힘들 것 같습니다. 그런데 사실 결국 DP에서 가장 중요한건 테이블 정의하고 점화식 찾는거고, 나중에 혼자서 DP 문제를 푸실 때에도 지금과 같은 막막함을 계속 느끼게 됩니다. 뭐 정답을 찾아보고 공부해도 되긴 하지만 매번 답에만 의존하는건 또 그렇게 좋은 방법은 아니니까 어떤 식으로 시도를 해볼 수 있는지 알려드리겠습니다. 어떤 식으로 해보냐면 직접 테이블을 채워보는 방법입니다.

일단 D[1]은 너무 자명하게 10입니다. D[i]의 정의에서 i번째 계단은 반드시 밟지 않을 계단으로 선택해야 한다는게 있기 때문입니다. D[2]는 S[2]의 값인 20입니다. 2번째 계단만 밟지 않으면 되기 때문입니다. D[3]도 S[3]인 15입니다. 이제 D[4]를 채우는게 핵심일 것 같은데, 일단 D[4]는 S[4]가 아니긴 합니다. 왜냐하면 4번째 계단만 안밟겠다고 해버리면 1, 2, 3번째 계단을 다 밟게 되는데 그러면 규칙에 위배됩니다. 그러면 1번째 계단을 안밟거나 2번째 계단을 안밟아야 하는데 어떤걸 안밟는게 더 이득인가 생각해보면 D[1]은 10인데 D[2]는 20이니 더 작은 D[1]을 이용하는게 낫습니다. 그래서 D[4]는 D[1] + S[4] = 35입니다.
D[5]도 같이 구해보면 마찬가지 논리로 2번째 계단을 안밟거나 3번째 계단을 안밟아야 하는데 D[3]이 D[2]보다 작으니 D[3]을 가져오면 됩니다. D[5]는 D[3] + S[5] = 15 + 10 = 25입니다.

이렇게 테이블을 직접 채우다보면 좀 감이 오기 마련인데, 이제 D[k]로 얘기를 해보면 k번째 계단을 밟지 않을거면 k-2번째나 k-3번째 계단 중 하나를 안밟아야 합니다. 그렇기 때문에 D[k-2] 혹은 D[k-3] 중에 작은걸 가져오면 됩니다. 그래서 D[k] = min(D[k-2], D[k-3]) + S[k]가 됩니다.

D[k]를 구할 때 D[k-3]이 쓰이니까 D[1], D[2], D[3]까지를 초기값으로 두면 됩니다. 이제 구현을 하면 되는데 D를 구한 것과 별개로 지금 답으로 뭘 출력해야하는지 고민해봅시다. N개의 계단이 있을 때 문제의 조건에서 마지막 도착 계단은 반드시 밟아야 한다고 했으니 가장 마지막으로 선택될 밟지 않은 계단은 N-1번째 계단이거나 N-2번째 계단입니다. 그래서 계단에 적힌 점수의 합에서 min(D[N-1], D[N-2])를 빼면 그게 정답입니다.

뭐 곧이곧대로 구현을 하면 되고 n이 2 이하일 땐 예외처리를 해줬습니다. 지금 이렇게 문제를 푸는 두 가지 방법을 살펴봤습니다. 참고로 본문에서는 언급하지 않았지만 D[i] = i번째 계단까지 올라섰을 때 점수 합의 최댓값, 단 i번째 계단을 반드시 밟아야 함으로 정의해서도 풀이가 가능합니다. 자세한건 문제집에 있는 별해 2 코드를 참고해보세요. 이렇게 관점을 달리 하면 또 다른 방식으로 DP식이 도출될 수도 있구나 하는걸 깨닫고 다음 문제로 가겠습니다.(코드 링크)
네 번째 문제는 BOJ 1149번: RGB 거리 문제입니다. 테이블을 먼저 고민해볼 때 D[i]를 i번째 집까지 칠했을 때의 최솟값으로 둔다면 점화식이 세워지지가 않습니다. 이웃한 집끼리는 색이 달라야 한다는 규칙이 있는데 방금 언급한 저 D[i]의 정의에서는 그 규칙을 고려하게끔 점화식을 만들 수가 없습니다.

그래서 테이블을 정의할 때 색상에 대한 정보가 추가적으로 들어가게끔 해야겠다는 생각이 들고, 위와 같이 정의를 하면 됩니다. 점화식은 제 생각에 그렇게 어렵지는 않게 세우실 수 있을 것 같은데 D[k][0], D[k][1], D[k][2]를 어떻게 나타낼지 한 번 고민해봅시다.

먼저 D[k][0]을 생각해보면 k번째 집을 빨강으로 칠할 예정입니다. 그러면 k-1번째 집은 초록 혹은 파랑이어야 하고 둘 중에 최소인걸 가져오면 됩니다. 그래서 D[k][0] = min(D[k-1][1], D[k-1][2]) + R[k]입니다. R[k]가 k번째 집을 빨강으로 칠할 때 드는 비용이란건 굳이 설명을 안해도 충분히 눈치챌 수 있겠죠? D[k][1], D[k][2]도 마찬가지로 표현할 수 있습니다.

이 문제에서는 초기값이 많이 단순한 편인데 그냥 D[1][0], D[1][1], D[1][2]만 채워두면 자연스럽게 해결됩니다. 점화식에서 D[k][...]을 계산할 때 D[k-1][...]만 있으면 됐기 때문입니다.

코드는 이렇게 생겼습니다. d[n][0], d[n][1], d[n][2] 중 최소를 출력하면 되는데 그걸 21번째 줄처럼 해도 되고 22번째 줄처럼 해도 됩니다.(코드 링크)

다섯 번째 문제는 BOJ 11726번: 2×n 타일링 문제입니다. 지금 이 단원에서 DP를 하고 있으니까 저 문제가 DP 문제이겠구나 싶긴 할텐데, 아무 정보 없이 문제를 접했다면 제 생각에 아마 절대 DP 문제라는걸 눈치채지 못했을 것 같습니다. 어렵겠지만 테이블은 제가 바로 알려드릴테니까 종이를 꺼내들고 직접 그려가면서 시도를 해보도록 합시다.

뭐 사실 시도를 해보라고 말은 하긴 했지만 아마 많이 어려웠을 것 같습니다. 같이 한 번 해보면, 지금 이 2×n칸을 채우는 방법의 수를 고민해볼건데 딴건 생각하지 말고 가장 왼쪽 위의 칸만 집중을 해보겠습니다. 굉장히 당연한 얘기를 해보면 가장 왼쪽 위의 칸은 결국 1×2 타일로 덮히거나 2×1 타일로 덮혀야 합니다.

먼저 2×1 타일로 덮어보겠습니다. 2×1 타일로 덮고났더니 남은건 2×n-1칸입니다. 이걸 채우는 방법의 수는 D[n-1]입니다. 즉 가장 왼쪽 위의 칸을 2×1 타일로 덮는 경우의 수는 D[n-1]이라는 것을 알 수 있습니다.

그 다음, 1×2 타일로 덮어보겠습니다. 덮고나면 뭔가 모양이 딱 직사각형으로 떨어지지 않습니다. 이대로 점화식을 세우는데 실패하고 마는 것인가..

그런데 가장 왼쪽 아랫칸을 보시면 이 칸을 덮는 타일은 무조건 정해져있습니다. 이렇게 1×2 타일로 덮을 수 밖에 없습니다. 이건 너무 당연한게 바로 윗 타일이 이미 덮혀버려서 가로로 연결하는 것 이외에는 달리 방법이 없습니다.
결과적으로 남은건 2×(n-2)칸이기 때문에 채우는 방법의 수는 D[n-2]입니다. 그러면 2×n칸을 채울 때 왼쪽 위의 칸을 2×1 타일로 덮으면 D[n-1]가지가 있고 1×2 타일로 덮으면 D[n-2]가지가 있으니 D[n] = D[n-1] + D[n-2]입니다. 뭔가 처음 봤을 땐 DP랑 크게 관련이 없어보이는 문제였는데 알고 봤더니 DP였습니다.

초기값을 어디까지로 할까 고민해보면 D[n]을 구할 때 D[n-2]까지가 필요하니 D[1]과 D[2]를 초기값으로 두는게 바람직합니다. 저 초기값과 식에서 알 수 있듯 이 값은 사실 피보나치 수열이 됩니다.
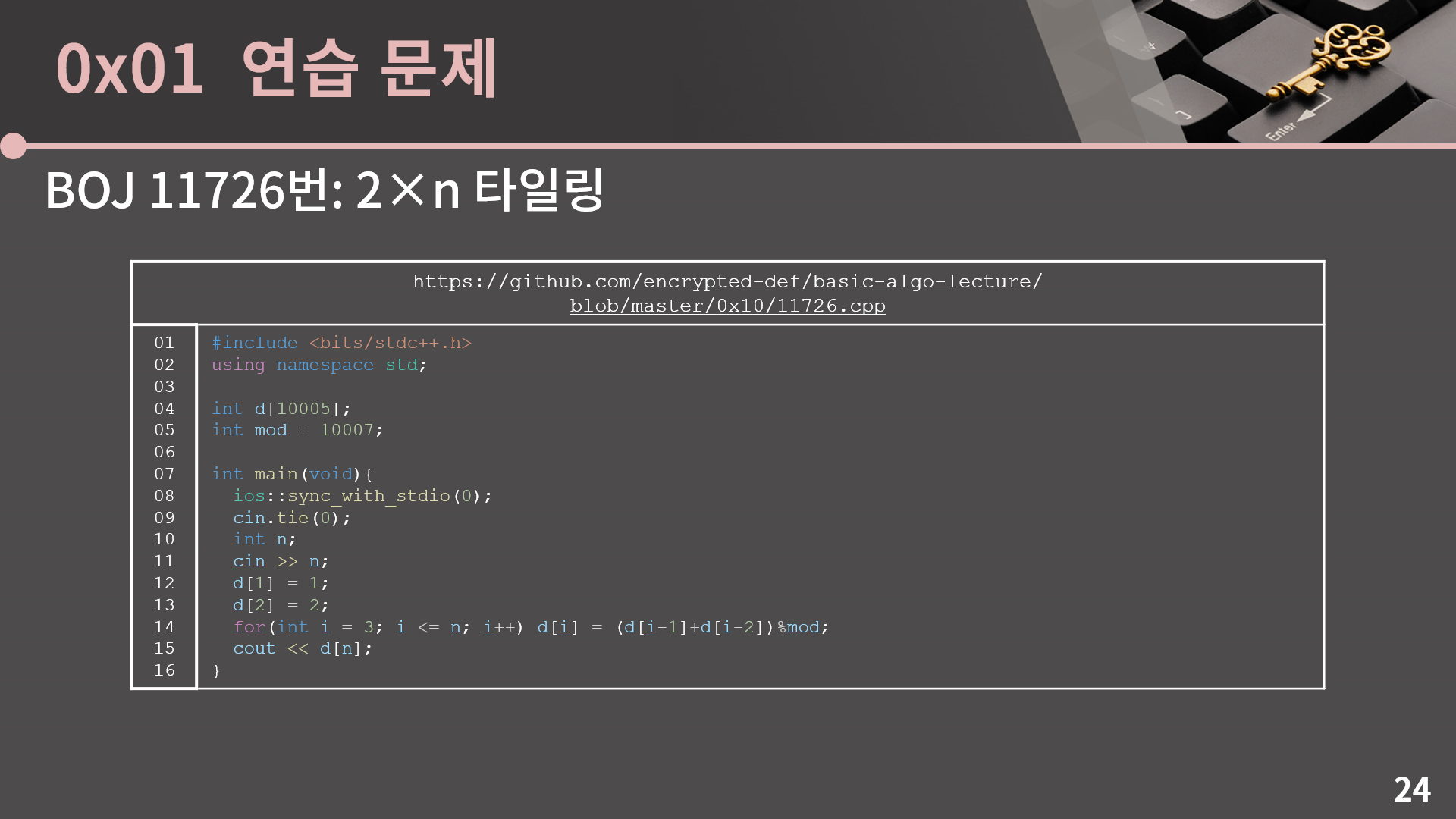
코드에서 별다른건 없는데 이런 문제에서 간혹 가다가 d[i] = d[i-1] + d[i-2]라고만 써놓고 제일 마지막에 d[i] % mod 를 출력하는 식으로 짜는 분이 있습니다. 그렇게 되면 계산 중간에 int overflow가 생겨서 틀리게 되니 지금 이 코드처럼 계산 중간 중간에 계속 10007로 나눈 나머지만을 가져가도록 해야합니다.(코드 링크)
여섯 번째 문제는 BOJ 11659번: 구간 합 구하기 4 문제입니다. 다른 무엇보다 지문이 짤막하다는 점에서 좀 마음에 듭니다. 이 문제도 이거랑 DP랑 무슨 상관이 있나 하는 생각이 들겠지만 이 문제를 통해 Prefix sum이라는 이름의 테크닉을 배울 수 있습니다.
일단 시간복잡도를 무시해보면 구현은 엄청 간단합니다. M번에 걸쳐서 들어오는 질의에 대해 A[i] + A[i+1] + ... + A[j]를 계산해서 출력하면 끝입니다. 그런데 시간복잡도를 생각하면 각 질의에서 최대 N번의 수를 더해야 합니다. 또 그러한 질의가 최대 M개 들어오니까 시간복잡도는 O(NM)입니다. N, M의 크기를 생각해봤을 때 N×M은 100억이니 어림도 없습니다. 그러면 뭔가 획기적인 방법이 필요하다란걸 느낄 수 있습니다.

일단 문제의 내용은 제쳐두고 D[i] = A[1] + A[2] + ... + A[i]로 정의하고 D 테이블을 채워보겠습니다. D[i]를 구할 때 매번 i개의 수를 더하려고 하면 D 테이블 전체를 채울 때 O(N2)이 필요하겠지만 D[i] = D[i-1] + A[i]인걸 이용하면 전체를 O(N)에 채울 수 있습니다.

그리고 이 D 테이블을 이용하면 A[i] + A[i+1] + ... + A[j] = D[j] - D[i-1]이 되어서 각 질의를 무려 O(1)에 계산을 할 수가 있습니다. 구현을 바로 해보도록 하겠습니다.

구현을 같이 살펴보면 수가 1,000 이하라고 했으니 100,000개를 더해도 int 범위 안에 잘 들어옵니다. 그래서 테이블은 int로 선언하면 됩니다.
다른 문제들에서는 0-indexed를 쓰나 1-indexed를 쓰나 별 상관이 없는데 이 문제에서는 1-indexed를 쓰는게 편합니다. 0-indexed를 쓰면 d[i-1]이 d[-1]이 되어버릴 수가 있어서 그것에 대한 예외처리를 따로 해줘야하는 불편함이 있습니다.
지금 이 문제에서는 대놓고 Prefix sum을 그대로 가져다 쓰면 되는 상황이었지만 Prefix sum을 문제를 푸는 과정에서 시간복잡도를 줄이는 기법 중 하나로 써먹는 경우도 종종 있어서 이 기법을 기억해두시면 좋겠습니다.
이렇게 총 여섯 개의 DP 문제를 다뤄봤습니다. 사실 DP 문제는 종류가 정말 많고 코딩테스트에 나올만한 수준으로 한정을 짓는다고 하더라도 2차원 DP, 테이블에 채우는 순서가 복잡한 DP 등과 같은 것들이 충분히 나올 수 있습니다. 그것들을 다 강의에서 다루고 싶었지만 이번 강의로 처음 DP를 접한 사람을 기준으로 할 때 너무 난이도가 확 뛰는 것 같아서 아쉽지만 같이 푸는 연습 문제는 여기까지만 하려고 합니다.
마지막으로 같이 하려고 하는건 DP에서 경로를 추적하는 방법이입니다. BOJ 12852번: 1로 만들기 2 문제를 보고 옵시다. 문제를 보면 단순히 값만 출력하는게 아니라 거쳐온 과정을 출력하라고 하고 있습니다. 이런 문제를 해결하려면 테이블을 채울 때 추가적인 정보를 어딘가에 기입해야 합니다.

원래 테이블을 값 테이블, 추가적인 정보가 들어갈 테이블을 경로 복원용 테이블이라고 부르겠습니다. 일단 D[1]이 0인건 당연하고 pre[1]은 어차피 참조가 안되는 값이라 큰 의미를 안두셔도 됩니다.

테이블에서 2번째 칸을 정할 때를 보면 2는 -1을 하거나 /2를 통해 1로 바뀔 수 있으니 D[2] = D[1] + 1로 계산이 됩니다. 그래서 @D[2]의 값은 1인데 이 때 pre[2]에 1을 적어줍니다. 이 1의 의미는 2에서 1로 가는게 최적이라는 의미입니다.

D[3]을 보면 3은 1 혹은 2로 바뀔 수 있는데 D[1]이 D[2]보다 작으니 D[3] = D[1] + 1로 계산됩니다. 그래서 D[3] = 1, pre[3] = 1입니다. 나머지들은 한번에 바로 보여드리겠습니다.

이렇게 경로 복원용 테이블을 다 구해놨으면 이 값을 가지고 1까지 도달하면 됩니다. 예를 들어 7을 생각해보면 6으로부터 왔다고 되어있으니 6으로 가고, 6에서는 3으로 가고, 3에서는 1로 가고 이렇게 7 6 3 1 이라는 경로를 찾아낼 수 있습니다. 구현을 바로 해봅시다.

테이블을 채우는건 이전에 풀었던 문제와 비슷하게 하면 되고 경로를 역추적하는건 기억하실지 모르겠는데 야매 연결 리스트를 구현할 때 원소들을 순회하던 상황과 비슷하게 생각하면 됩니다.
지금 이 문제와 같이 단순히 DP에서 값만 출력하는 것이 아니라 값을 얻은 경로가 필요한 상황이라면 내 값이 어디서부터 온 것인가를 따로 저장한 후 나중에 경로를 복원하면 됩니다. 참고로 똑같은 원리로 BFS에서도 경로 복원이 가능합니다.

이렇게 DP도 마무리가 됐습니다. 배경 사진 너무 멋있지 않나요? 전 18년에 친구랑 북유럽 가서 오로라 보고왔는데 정말 추웠지만 또 정말 예뻤어서 또 가고 싶습니다.
마지막으로 정리를 해보겠습니다. 코딩테스트에서 DP 문제가 나오면 오늘 문제들을 풀면서 느끼셨듯이 보통은 구현이 쉽습니다. 그래서 풀이를 찾아내기만 하면 아주 편하게 문제를 넘길 수 있는데 테이블을 잡고 식을 세우는게 쉽지 않습니다. 또 사실 연습이 부족하면 주어진 문제가 DP로 풀 수 있는 문제라는 것 자체를 눈치채지 못할 수도 있습니다. 그러면 어떻게 하면 되냐라고 했을 때 그냥 진짜 많이 풀면서 테이블을 잡고 식을 세우는 과정을 반복학습하면 됩니다. 처음엔 식이 잘 안잡혀서 풀이를 찾아보는 일이 많겠지만 별의별 희한한 테이블과 점화식을 많이 접해보고 나면 어느샌가 문제를 마주했을 때 감각적으로 테이블을 잡고 점화식을 세우게 되는 자신을 볼 수 있을 것입니다. DP는 양이 정말 많은만큼 잊을만하면 한 두 문제씩 꾸준하게 풀어두면 좋습니다. 그럼 고생 많으셨습니다.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x13강 - 이분탐색 (63) | 2021.07.26 |
|---|---|
| [실전 알고리즘] 0x12강 - 수학 (45) | 2021.06.30 |
| [실전 알고리즘] 0x11강 - 그리디 (47) | 2021.02.17 |
| [실전 알고리즘] 0x0F강 - 정렬 II (44) | 2021.01.14 |
| [실전 알고리즘] 0x0E강 - 정렬 I (33) | 2020.10.09 |
| [실전 알고리즘] 0x0D강 - 시뮬레이션 (165) | 2020.07.17 |