
안녕하세요 여러분, 드디어 올 것이 왔습니다. 마음의 준비를 단단히 하셔야 합니다.. 드디어 실전 알고리즘 강의에서 첫 번째 고비에 도달했는데 이 강의와 함께 이번 고비를 잘 헤쳐나가면 좋겠습니다.

0x05까지 있으니 목차를 보시면 뭐가 되게 많죠? 사실 리뉴얼 하기 전의 강의에서는 기본적인 BFS만 다뤘는데 늘 내용을 보충하고 싶었습니다. 그래서 리뉴얼한 강의에서는 BFS의 다양한 응용 내지는 유형들을 전부 짚고 넘어갈 것입니다.

BFS를 알아보기 전에 우리에게 익숙한 문제를 가지고 얘기를 시작해보겠습니다. 대충 물고기 사진을 하나 가져왔는데, 그림판의 페인트 기능을 이용하면 물고기의 색을 바꿀 수가 있습니다. 페인트 기능은 외부 윤곽선을 따라서 구분되는 영역의 색을 한꺼번에 바꾸는 거고, 이런걸 Flood Fill이라고 부르기도 합니다.
그런데 이 Flood Fill 기능은 어떻게 구현할 수 있을까요? 일단 클릭한 칸의 상하좌우를 보여 나와 색이 같은지 확인하고, 같은 칸에 대해서 또 상하좌우로 확인하고… 뭔가 좀 막연합니다. 지금까지 배운 지식으로는 이 기능을 구현하는 게 쉽지 않지만, 이번에 배울 BFS라는 알고리즘을 가지고 해결할 수 있게 됩니다.

그래서 계속 BFS BFS하는데 도대체 그게 뭔가 하면, 여기 적힌 대로 다차원 배열에서 각 칸을 방문할 때 너비를 우선으로 방문하는 알고리즘입니다. 그런데 BFS라는 단어가 굉장히 낯설 텐데 저 표현을 보고 나면 저 혼란스러울 것 같습니다. 대체 너비를 우선으로 방문한다는 게 뭔 소리지… 싶을텐데, 달리 어떻게 설명할 방법이 없습니다.
왜냐하면 원래 BFS는 그래프라는 자료구조에서 모든 노드를 방문하기 위한 알고리즘입니다. 여기서 말하는 그래프는 우리가 흔히 아는 왼쪽과 같은 형태의 그래프가 아니라 오른쪽 모양의 그래프이고, 정확한 정의는 정점과 간선으로 이루어진 자료구조입니다.
그렇기 때문에 BFS를 정확하게 이해하려면 그래프 자료구조에 대한 이해가 선행되어야 하는데 그건 배보다 배꼽이 더 큰 느낌입니다. 그래서 BFS를 엄밀하게 정의할 수는 없지만, 실제로 어떻게 동작하는지를 보면서 다차원 배열에서의 BFS를 이해해보도록 하겠습니다.

이전 강의 자료에서는 마치 설명서처럼 일단 방법을 글로 먼저 설명해두었는데 생소한 내용이다 보니 설명을 봐도 전혀 감이 안 올 것 같습니다. 그래서 그냥 실제 BFS를 돌리는걸 한 번 보고 가겠습니다. 저희의 목표는 (0, 0)과 상하좌우로 이어진 모든 파란색 칸을 확인하는 것입니다. 이 문제를 BFS로 어떻게 해결하는지 보겠습니다.

우선 BFS 알고리즘에서는 좌표를 담을 큐가 필요합니다. BFS 알고리즘이 시작되면 우선 (0, 0)에 방문했다는 표시를 남기고 해당 칸을 큐에 넣습니다. 이 초기 세팅이 끝난 후에는 큐가 빌 때까지 계속 큐의 front를 빼고 해당 좌표의 상하좌우를 살펴보면서 큐에 넣어주는 작업을 반복하게 됩니다.

지금 상황에서 큐의 front는 (0, 0)이고 pop을 합니다. 그리고 (0, 0)의 상하좌우 칸을 보는데, 이 중에서 우리는 파란색 칸이면서 아직 방문하지 않은 칸을 찾을 것입니다.

지금 상황을 보면 (0, 0)과 상하좌우로 인접한 (0, 1)과 (1, 0)은 모두 파란 칸이면서 아직 방문하지 않았습니다. 이 2개의 칸에 방문했다는 표시를 남기고 큐에 넣습니다.

(0, 0)에서 할건 다 했고, 다음으로 넘어갑니다. 현재 큐의 front는 (0, 1)이고 pop을 합니다. 참고로 (0, 1)에서 0은 행을 의미하고 1은 열을 의미합니다. 그리고 이번에도 (0, 1)의 상하좌우 칸을 확인합니다. 이 칸들 중에서 (0, 0)은 파란 칸이지만 이미 방문을 했고, (1, 1)은 빨간 칸입니다. 유일하게 (0, 2)만 파란색 칸이면서 아직 방문하지 않은 칸이니까 (0, 2)에 방문했다는 표시를 남기고 큐에 넣습니다.
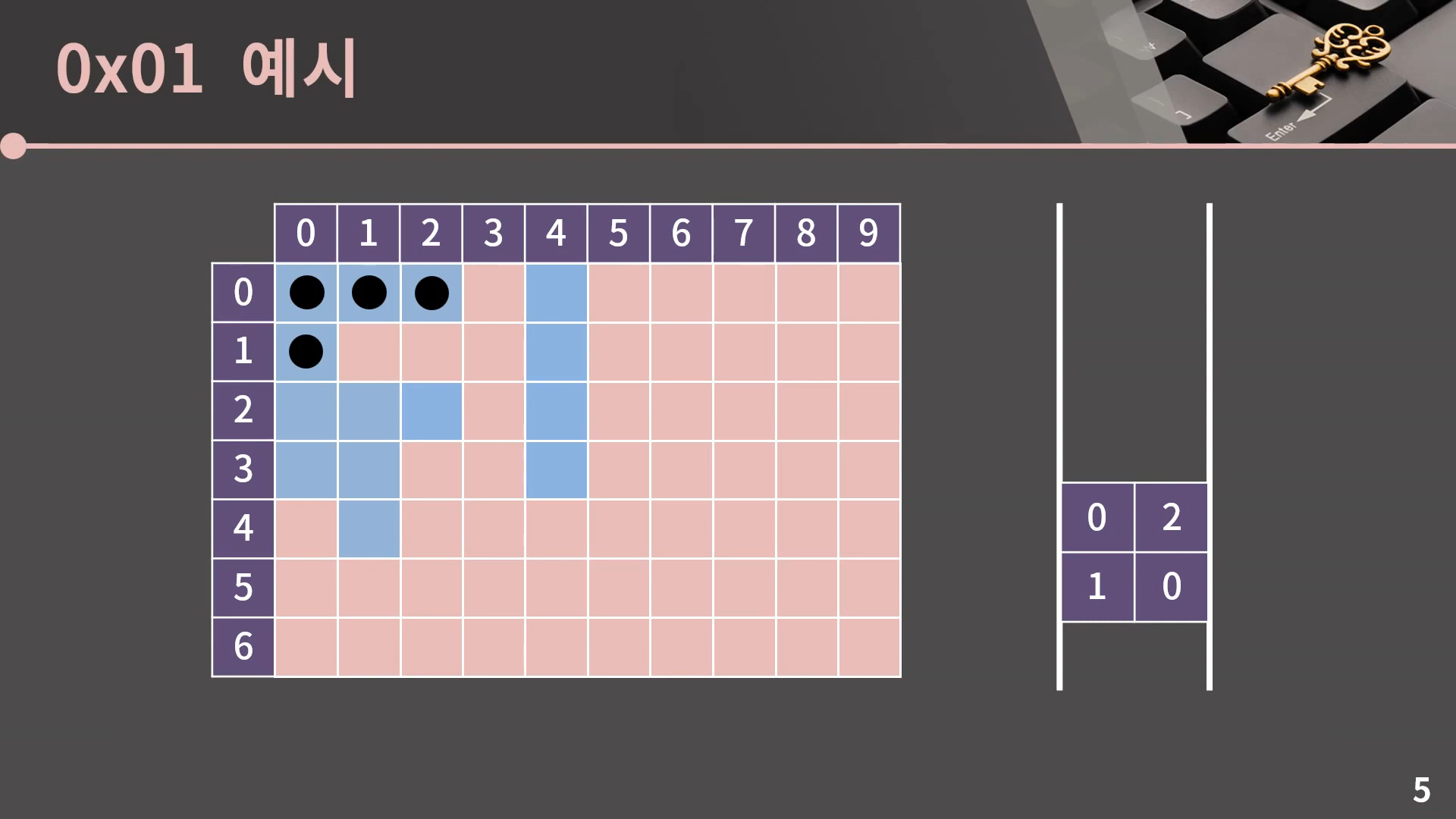
계속 이런식으로 큐의 front를 pop하고 인접한 칸 중에서 방문하지 않은 파란색 칸에 표시를 남기고 큐에 넣어주면 되는데, 이후로는 한 번에 쭉 보여드릴 테니 아래의 예시를 확인해봅시다.


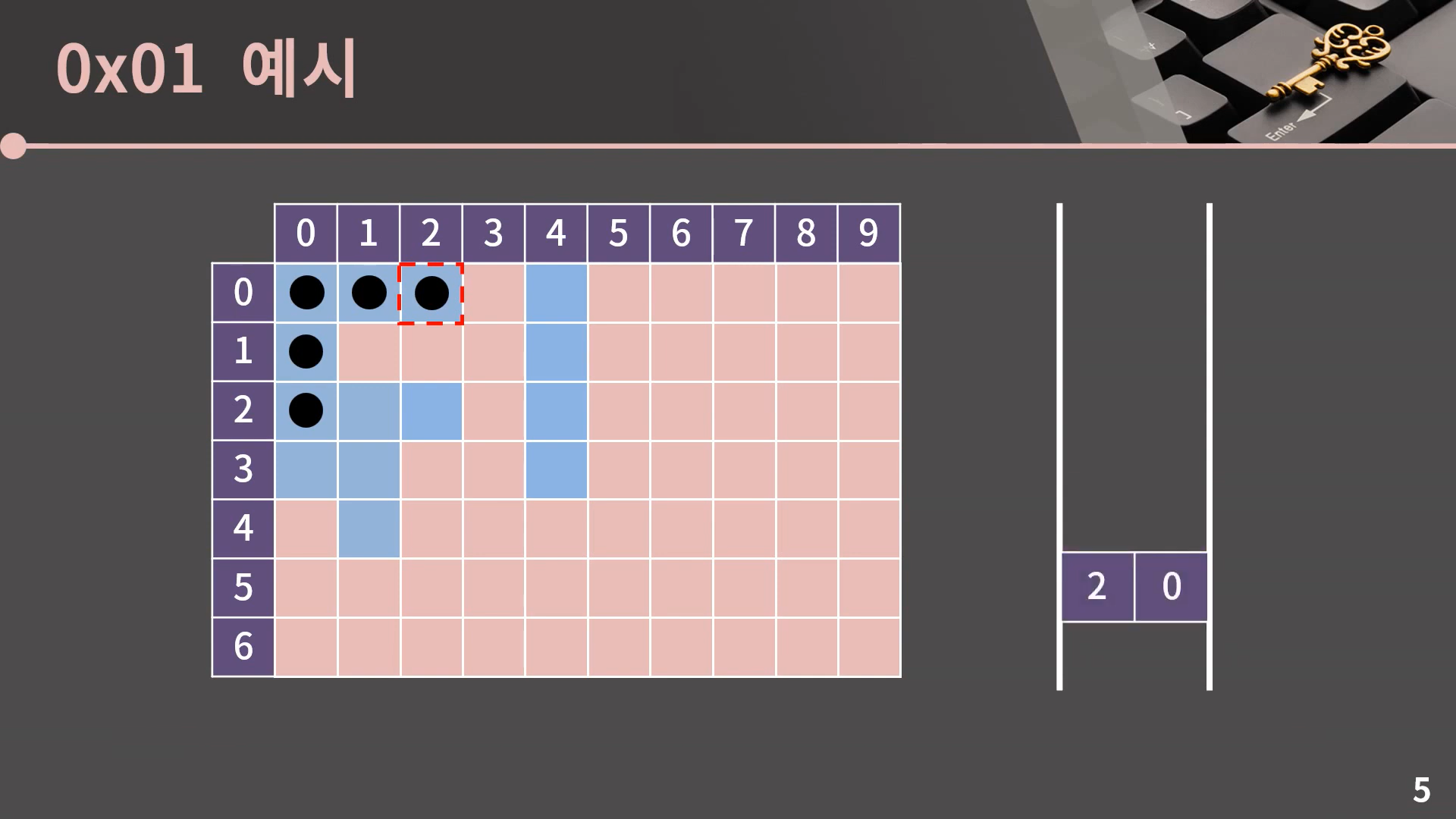
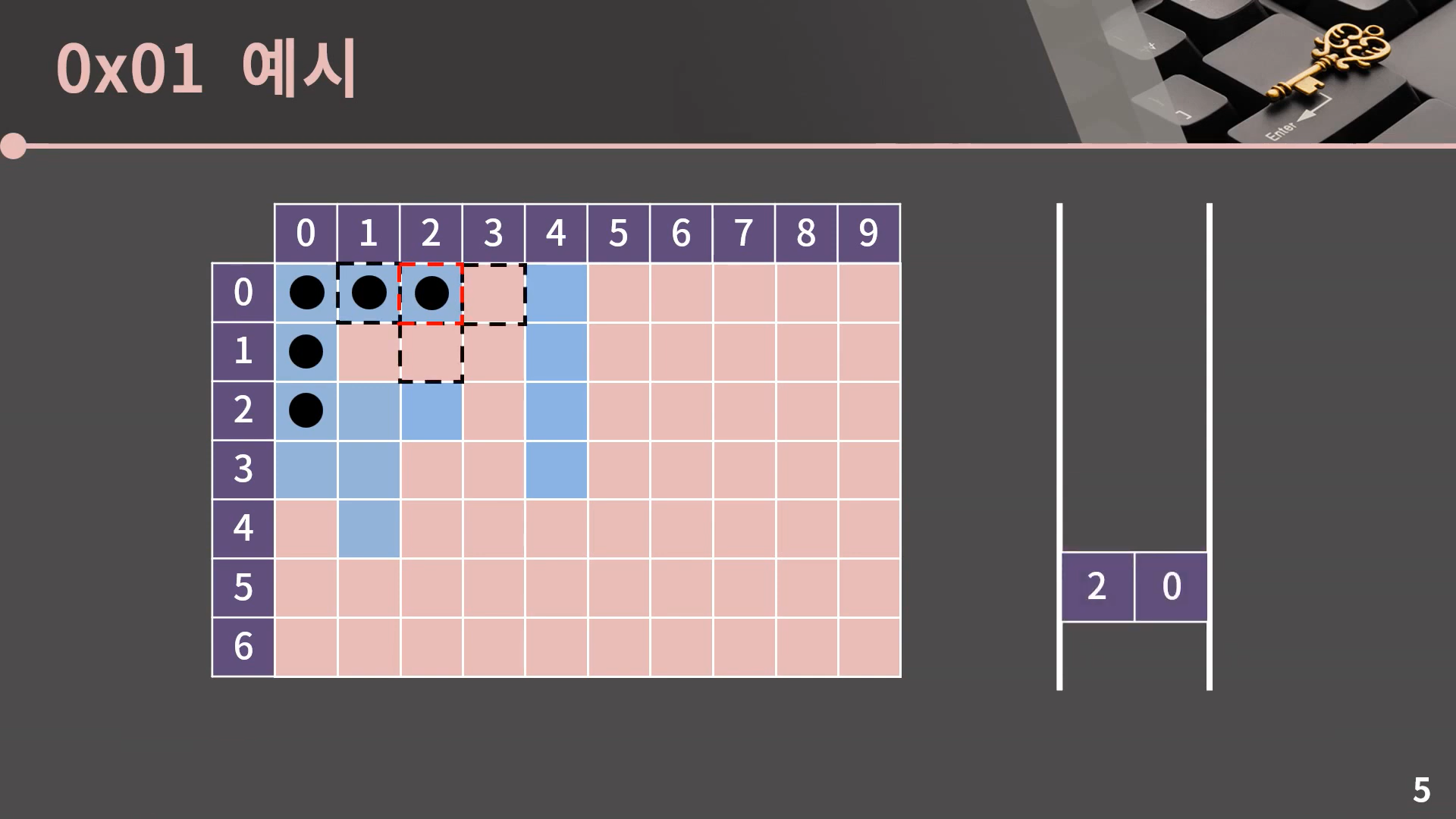
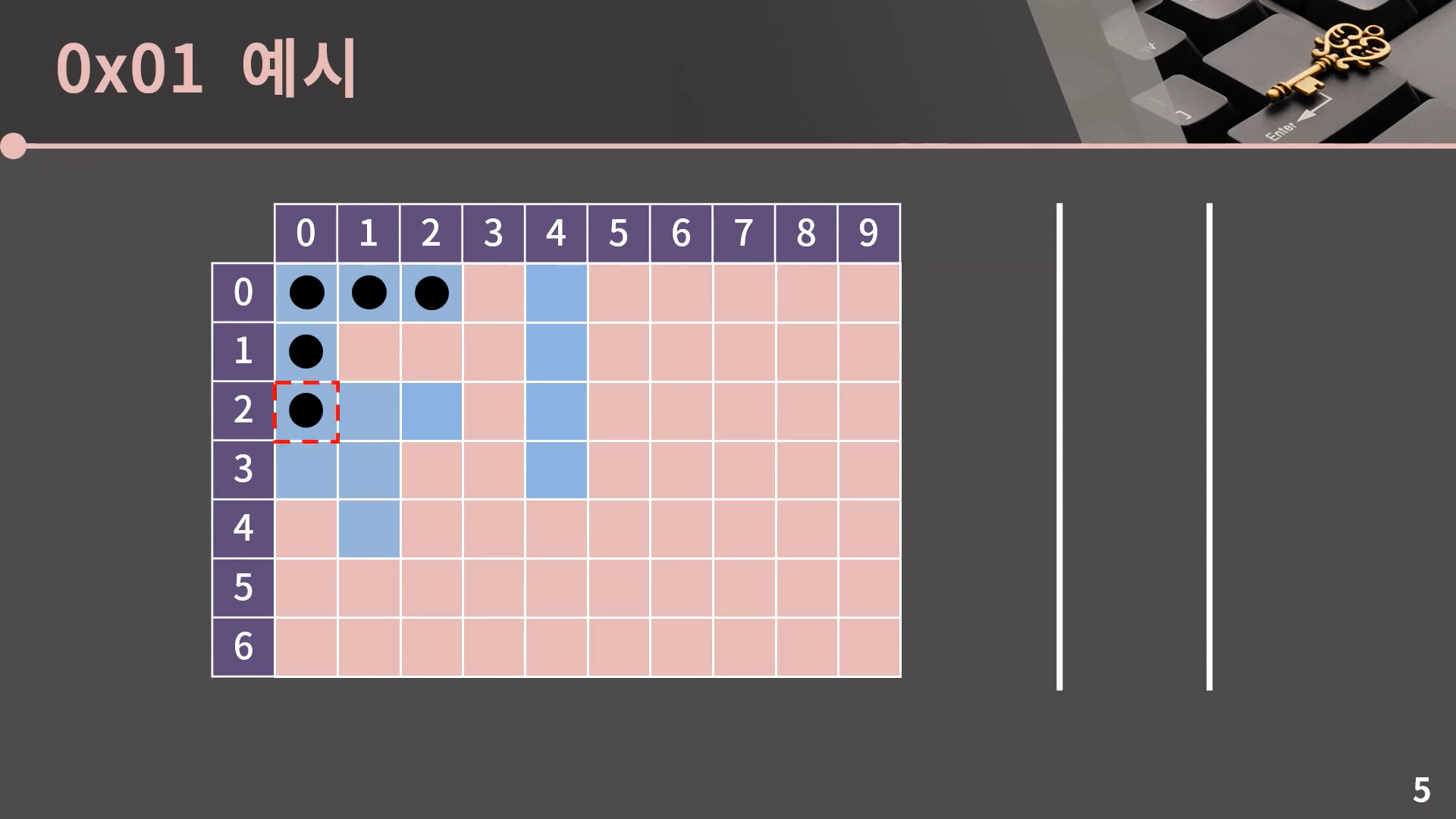
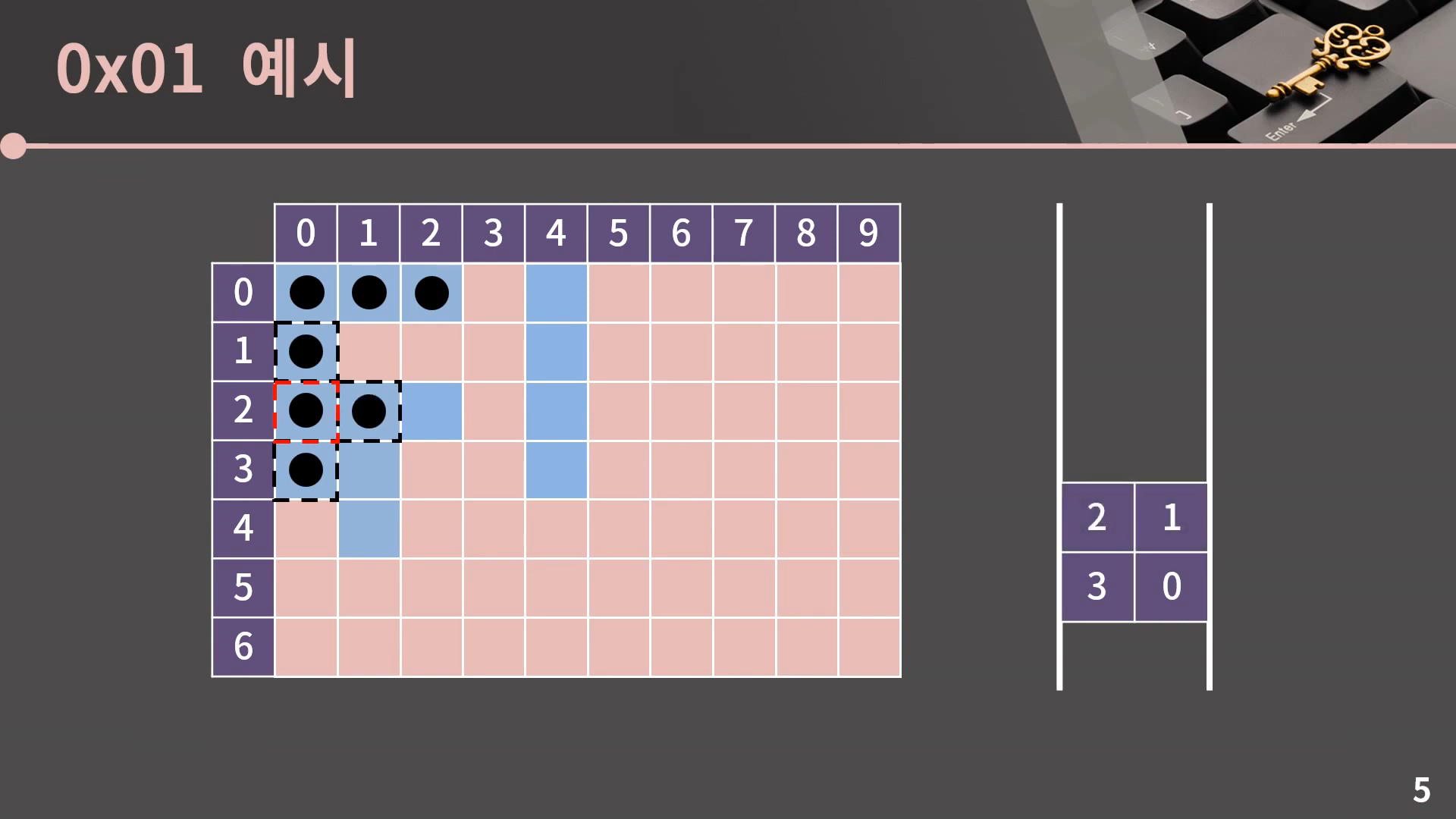
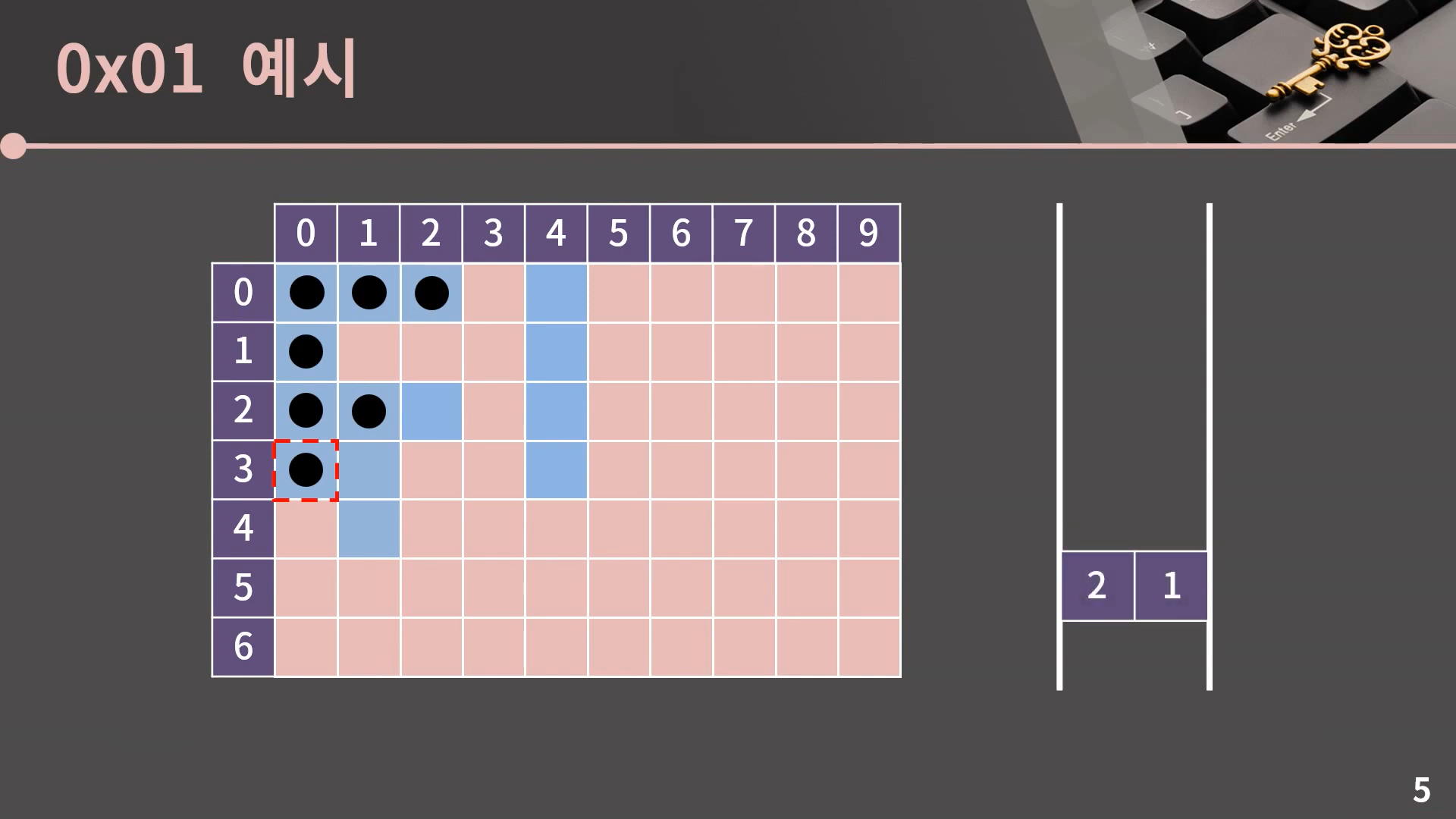



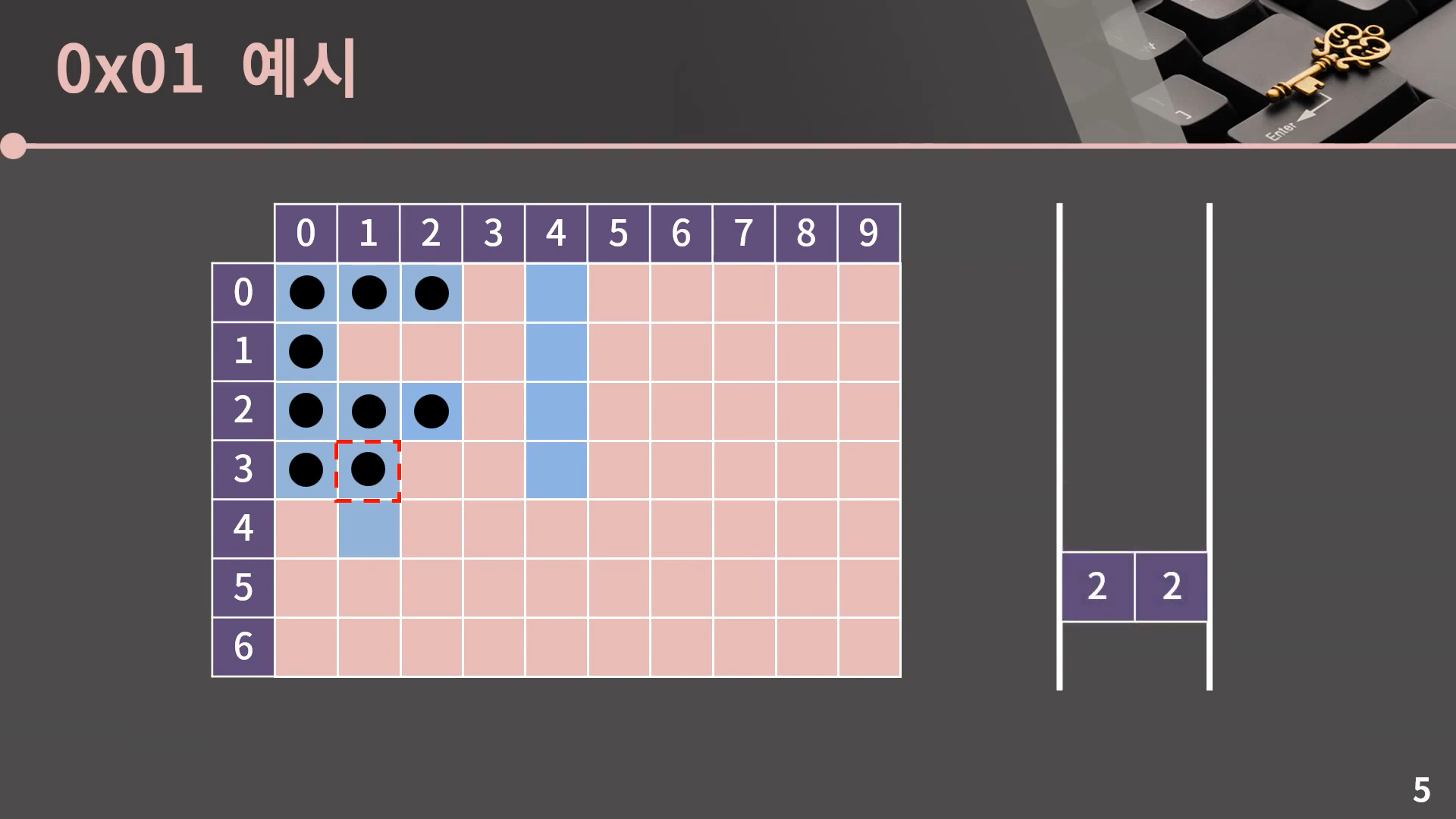

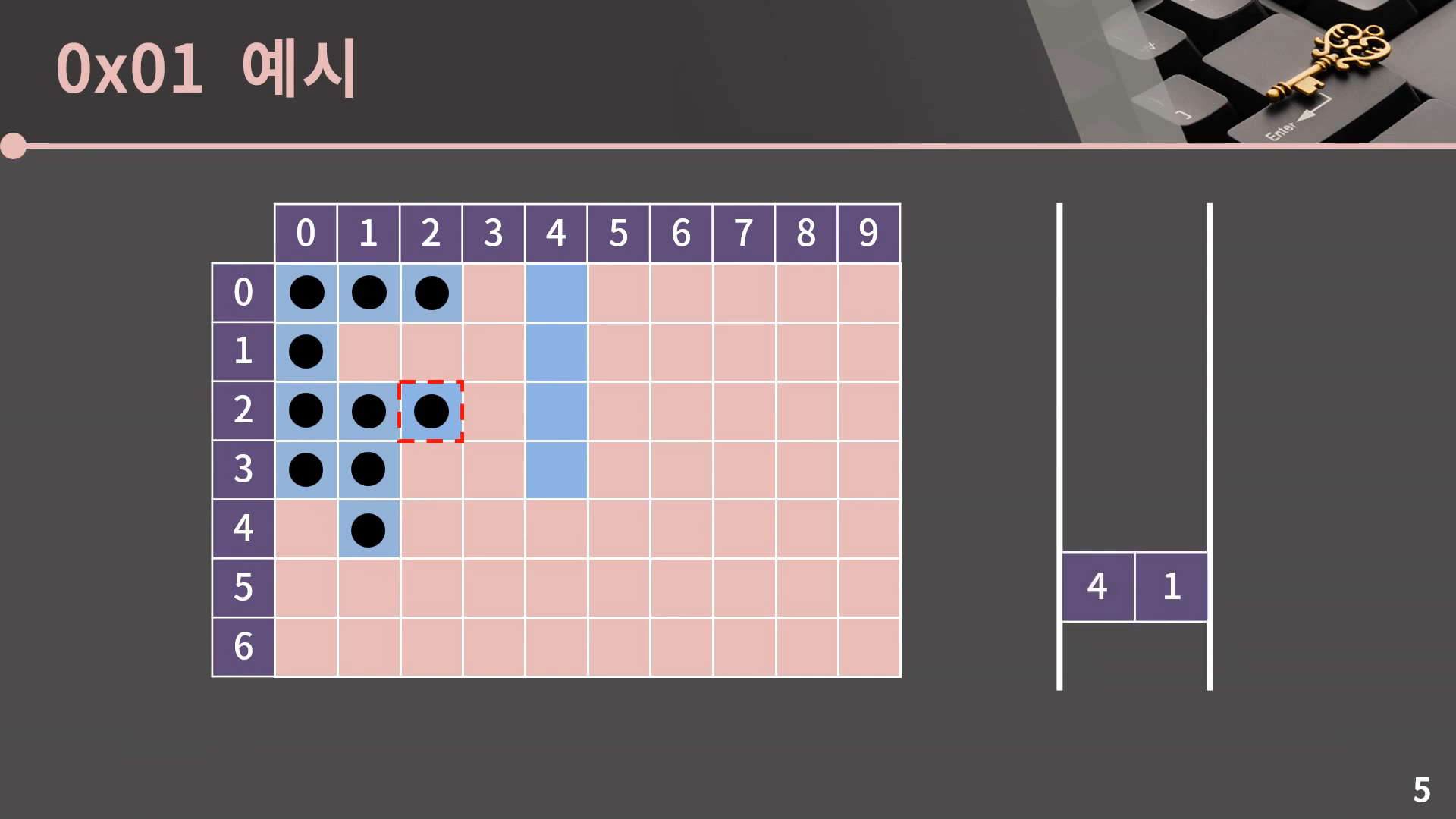
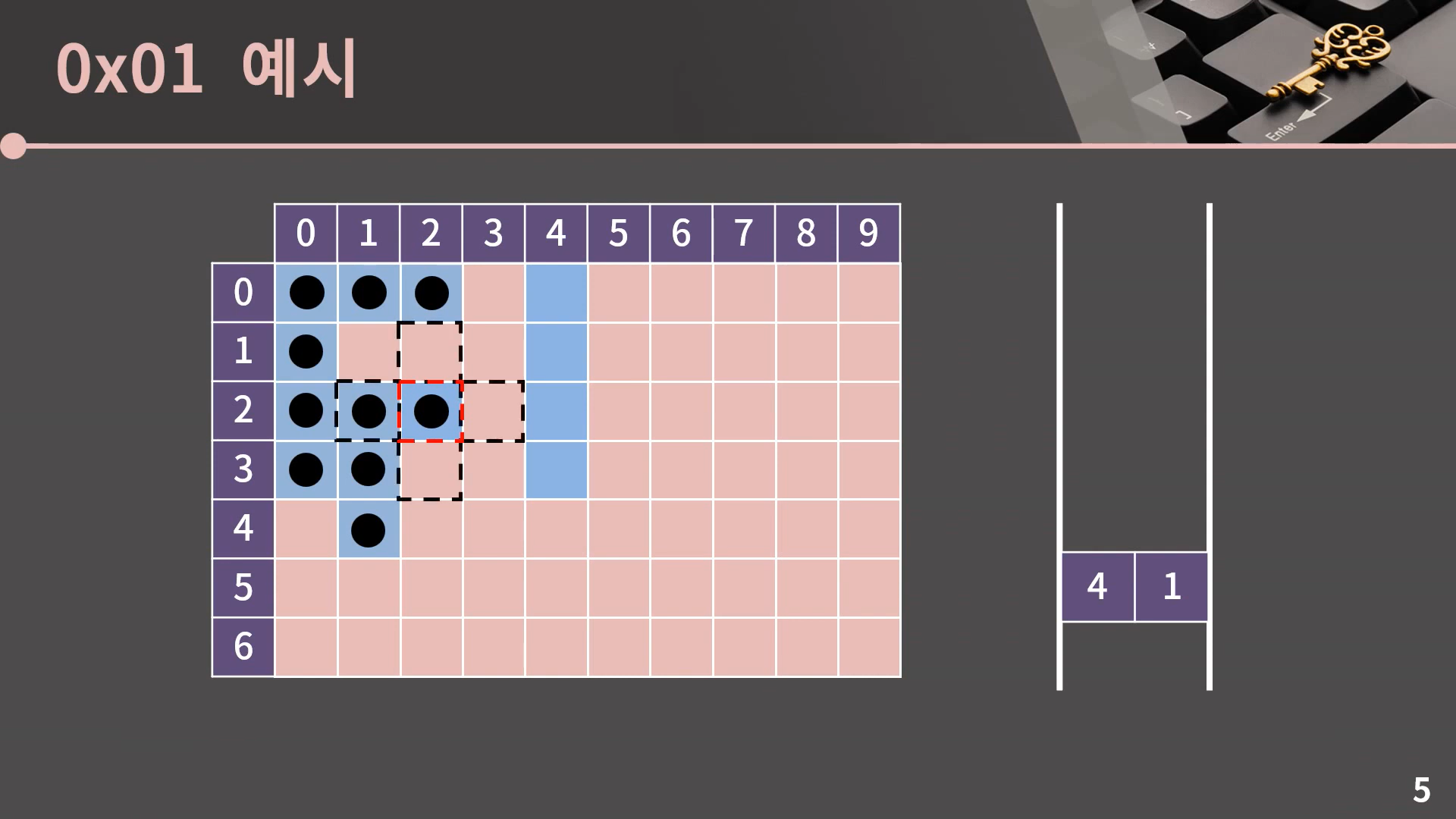
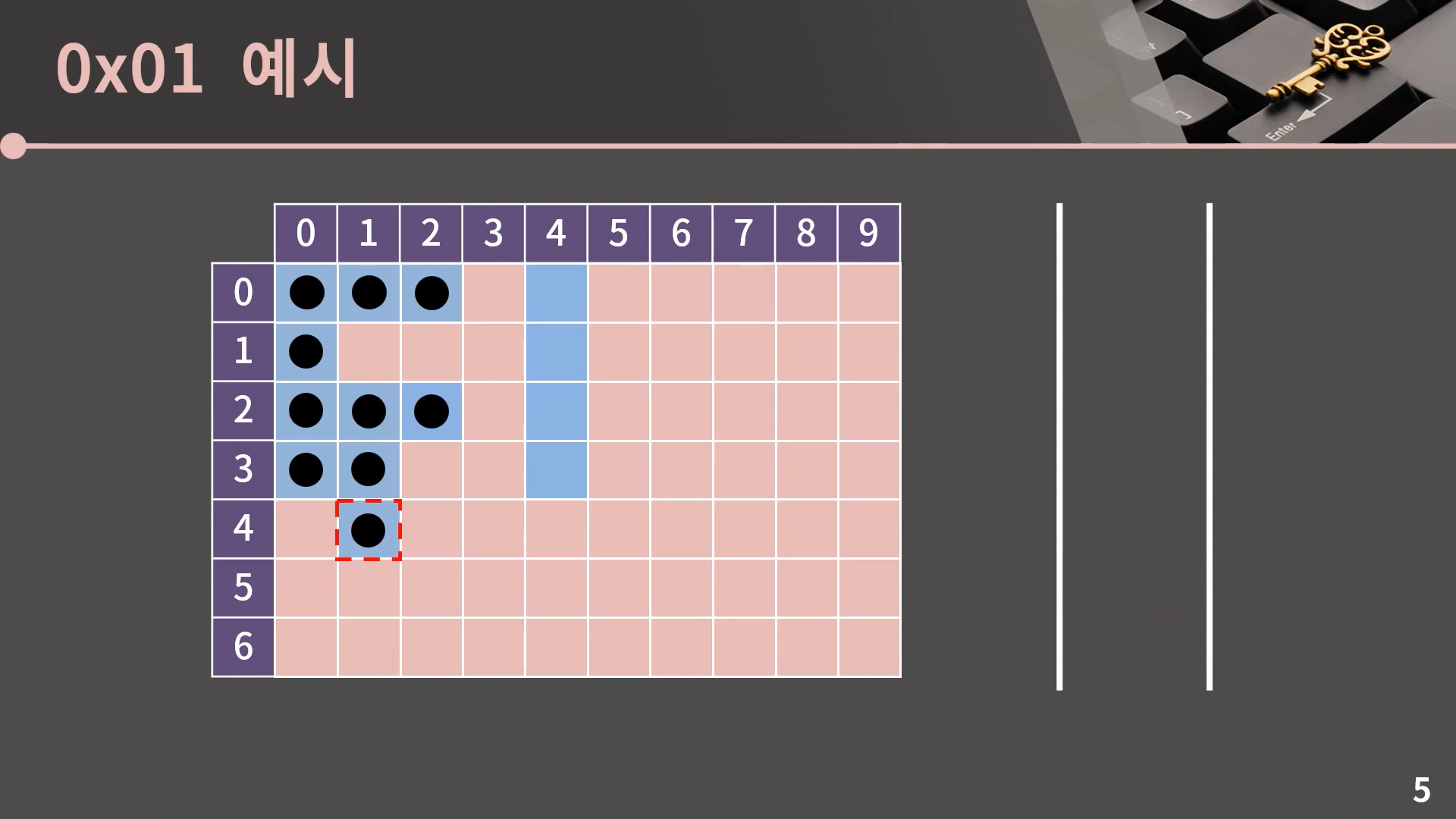


이렇게 큐가 빈 순간 과정은 종료되고 (0, 0)과 상하좌우로 이어진 모든 파란 칸을 잘 방문했음을 알 수 있습니다.

이렇게 BFS 과정을 같이 살펴봤는데 이해가 잘 가실지 모르겠습니다. 이제 과정을 step by step으로 설명드리겠습니다. 일단 시작하는 칸을 큐에 넣고 방문했다는 표시를 남깁니다. 그리고 큐가 빌 때까지 큐에서 원소를 꺼내고 상하좌우로 인접한 칸에 대해 처음으로 방문했다면 해당 칸을 큐에 삽입하는 것을 반복하면 됩니다.
BFS의 시간복잡도를 생각해보면 방문 표시를 남기기 때문에 모든 칸은 큐에 1번씩만 들어가게 됩니다. 그렇기 때문에 시간복잡도는 칸이 N개일 때 O(N)이 됩니다. 만약 행이 R개이고 열이 C개이면 O(RC)가 될 것입니다.

BFS의 구현을 다루기 전에 코드에서 쓰이게 될 STL을 하나 소개해드리겠습니다. 바로 utility 헤더에 있는 pair인데, pair를 이용하면 두 자료형을 묶어서 가지고 다닐 수 있습니다. make_pair로 값을 넣어줄 수도 있고, C++11 이상에서는 그냥 중괄호를 써서 쉽게 해결할 수 있습니다.
값의 접근은 각각 first, second를 부름으로서 가능하고 또 pair에는 미리 대소 관계가 설정되어 있어서 편합니다. 알아서 앞쪽의 값을 먼저 비교하고, 이후 뒤쪽의 값을 비교합니다.
BFS를 구현할 때 큐에 좌표를 넣어야 하는데, 이때 pair를 쓸 것입니다. (레퍼런스 링크, 예제 링크)

이제 BFS를 코드로 어떻게 짜면 될지 고민해보겠습니다. 앞에서 본 것과 같이 큐에서 원소를 빼고 상하좌우의 칸을 확인하는 식으로 구현하면 되는데, 아마 직접 짜 보려고한다면 아마 굉장히 비효율적으로 짜게 될 것입니다. 직접 시도해보는 것도 정말 좋은 자세이지만 BFS는 어느 정도 정석적인 구현이 있어서 지금 보여드릴 코드를 거의 외우다시피 해도 괜찮습니다. 특히 삼성 A형을 치기 위해서는 BFS가 정말 숙달되어 있어야 하는데, 어느 정도냐면 자고 있다가 누가 툭 쳐서 BFS를 짜라고 시켜도 한 5분 내로 기본 틀을 좌르륵 쳐낼 수 있어야 합니다.
일단 코드를 보겠습니다. 공간이 좁아서 주석을 많이 뺐는데, 저기 깃헙 링크에 들어가서 정확하게 코드를 확인해보는 걸 추천드립니다. 아무튼 코드가 굉장히 낯설 텐데 같이 이해를 해보겠습니다.
일단 03, 04번째 줄에서 #define을 해놓은 건 pair를 조금 더 편하게 쓰기 쓰기 위함인데, first/second 대신 t.X/t.Y로 쓰고 싶어서 저렇게 했습니다.
그다음 쭉 있는 변수들의 역할이 궁금할 텐데 하나씩 설명을 드리겠습니다. board는 말 그대로 판을 의미합니다. 1이면 파란 칸이고 0이면 빨간 칸이라고 생각하면 됩니다. 그리고 vis는 방문 여부를 저장할 변수입니다. 칸 위에 올리던 동그라미를 코드 상에서는 vis 값을 1로 변경함으로써 처리하는 것입니다. 그리고 n과 m은 각각 행과 열의 개수를 의미하고, dx와 dy는 상하좌우를 영리하게 처리하기 위한 변수인데 이건 실제로 쓰일 때 설명을 드리겠습니다.
그 후로 (0, 0)에 방문 표시를 하고 큐에 추가하는 과정이 코드에서는 14, 15번 줄이 됐습니다. 그다음에는 큐가 빌 때까지그 상하좌우의 칸을 추가하는걸 쭉 반복하는데, 일단 큐의 front를 cur에 저장하고 pop을 합니다. 그다음 줄은 그냥 방문 순서를 나타내 주기 위해서 넣은 출력문입니다.
19번째 줄에서 26번째 줄까지의 루틴이 좀 중요한 루틴입니다. 아까 정체를 알 수 없던 dx, dy가 여기서 쓰입니다. 판에서 저희가 상하좌우를 생각해보면 오른쪽 아래의 그림과 같습니다. 그런데 노파심에 말을 하자면, 이 코드에서 x가 행을, y가 열을 의미합니다. 그런데 사람에 따라 x가 열이고 y가 행인 게 더 익숙할 수 있습니다. 이게 별게 아닐 수 있지만 생각을 할 때 굉장히 헷갈리게 하는 요소가 될 수 있습니다. 당장 지금 저 그림도 만약 x가 열이고 y가 행이라면 왼쪽 칸이 x-1, y가 되어야 합니다. 뭐 어떻게 하든 답은 잘 나오겠지만 저 뿐만 아니라 대부분의 BFS 코드에서 x가 행을, y가 열을 의미하는 경우가 많았어서 이 방식으로 따라오시는게 좋을 것 같습니다.
아무튼 우리는 (cur.X, cur.Y)에 대해 상하좌우 칸인 (cur.X-1, cur.Y), (cur.X, cur.Y-1), (cur.X, cur.Y+1), (cur.X+1, cur.Y)를 확인할 필요가 있습니다. 그리고 이걸 쉽게 하는 방법이 바로 19번째 줄부터 이어지는 for문인데, nx와 ny의 값을 같이 봅시다. 보면 cur.X, cur.Y에 dx[dir], dy[dir]을 각각 더하죠? 그리고 08, 09번째 줄로 시선을 돌려보면 dx[dir], dy[dir] 값이 (1, 0), (0, 1), (-1, 0), (0, -1)이니까 nx, ny에 상하좌우의 좌표값이 깔끔하게 담긴다는 것을 알 수 있습니다. dx, dy 값에 따른 순서는 아랫쪽, 오른쪽, 윗쪽, 왼쪽 순서이긴 한데 이건 크게 중요하지는 않습니다.
이후 22번째 줄에서 일단 범위에 들어오는지를 확인하고, 23번째 줄에서 이미 방문했거나 파란 칸이 아닌 경우를 걸러내고 난 후에는 방문했다는 표시를 vis[nx][ny] = 1로 바꿈으로서 남기고 큐에 추가해주면 됩니다. 만약 22번째 줄과 23번째 줄의 순서가 바뀌면 어떻게 될까요? 그렇게 되면 vis[-1][0]과 같은 값을 참조할 수 있어서 런타임에러가 날 수 있습니다. 그렇기 때문에 일단 범위 내에 들어오는지를 꼭 먼저 확인한 후에 vis, board 배열값을 봐야합니다.

제 코드를 보기 전에 BFS를 먼저 구현해보려고 시도해보셨다면 아마 높은 확률로 뭔가 비효율적이거나 잘못 동작하는 코드를 짰을 것입니다. 조금만 익숙해지면 그냥 정석적인 구현을 거의 복붙하다시피 할 수 있겠지만 그래도 구현을 시도해보실 분들을 위해 자주 실수하는 점들을 몇 개 짚고 가겠습니다.
첫 번째로, 시작점을 큐에 넣긴하는데 정작 방문했다는 표시를 남기지 않은 채로 진행하는 경우가 있습니다. 이렇게 되면 시작점을 두 번 방문할 수가 있습니다.
두 번째는 큐에 넣을 때 해당 칸에 방문했다는 표시를 남기지 않고 큐에서 빼낼 때 남기는 경우인데, 이렇게 되면 같은 칸이 큐에 여러 번 들어가게 되어서 시간 초과나 메모리 초과가 발생할 수 있습니다. 특히 이건 보통 예제로 주는 작은 케이스에서는 잘 돌아가다가 실제 제출을 했을 때 터지는 경우가 많기 때문에 주의해야 합니다.
세 번째는 앞의 코드에서 있던 nx, ny가 배열 바깥으로 벗어났는지에 대한 루틴을 아예 빼먹었거나, 아니면 이상하게 구현을 한 상황을 말합니다.
직접 짠 BFS가 좀 이상하면 이런 점들을 체크해볼 수 있겠죠?

지금부터 BFS를 이용해서 해결할 수 있는 문제를 살펴보도록 하겠습니다. BOJ 1926번 그림 문제를 확인해보겠습니다.
우리는 지금 하나의 시작점에서 BFS를 도는 방법만 익혔는데 이 문제에서는 주어진 도화지에서 모든 그림을 찾아야하고, 크기도 알아내야 합니다. 꽤 어려운게 아닌가 싶을수도 있는데 지금 이 문제 정도면 BFS의 기본 예제 정도라고 생각하시면 됩니다. 쉽지는 않겠지만 한 번 고민해보는 시간을 가지도록 하겠습니다. 먼저 도전해보셔도 괜찮습니다.
그런데 사실 오늘 처음 BFS를 배웠으면 어려운게 당연한거라, 도움이 될만한 팁을 살짝 드려보겠습니다. 결국 이 문제를 해결하기 위해 우리가 해야할 일은 상하좌우로 연결된 그림의 크기를 알아내기, 도화지에 있는 모든 그림을 찾아내기 이 2개입니다.
첫 번째의 경우는 크게 어렵지는 않은게, 그냥 큐에서 pop을 몇 번 하는지만 세면 끝입니다.
문제는 두 번째인데, 우리는 지금 어떤 한 시작점과 이어진 그림만 찾아내는 법만 알고 있기 때문에 뭔가 고민을 좀 해볼 필요가 있습니다.
지금 나타낸 그림은 주어진 예제인데, 여기 있는 4개의 그림을 어떤 식으로 찾아야할까요? 이 부분은 이중 for문을 돌면서 BFS의 시작점이 될 수 있는 곳을 찾으면 됩니다. 무슨 소린가 싶을텐데 이런 느낌입니다.
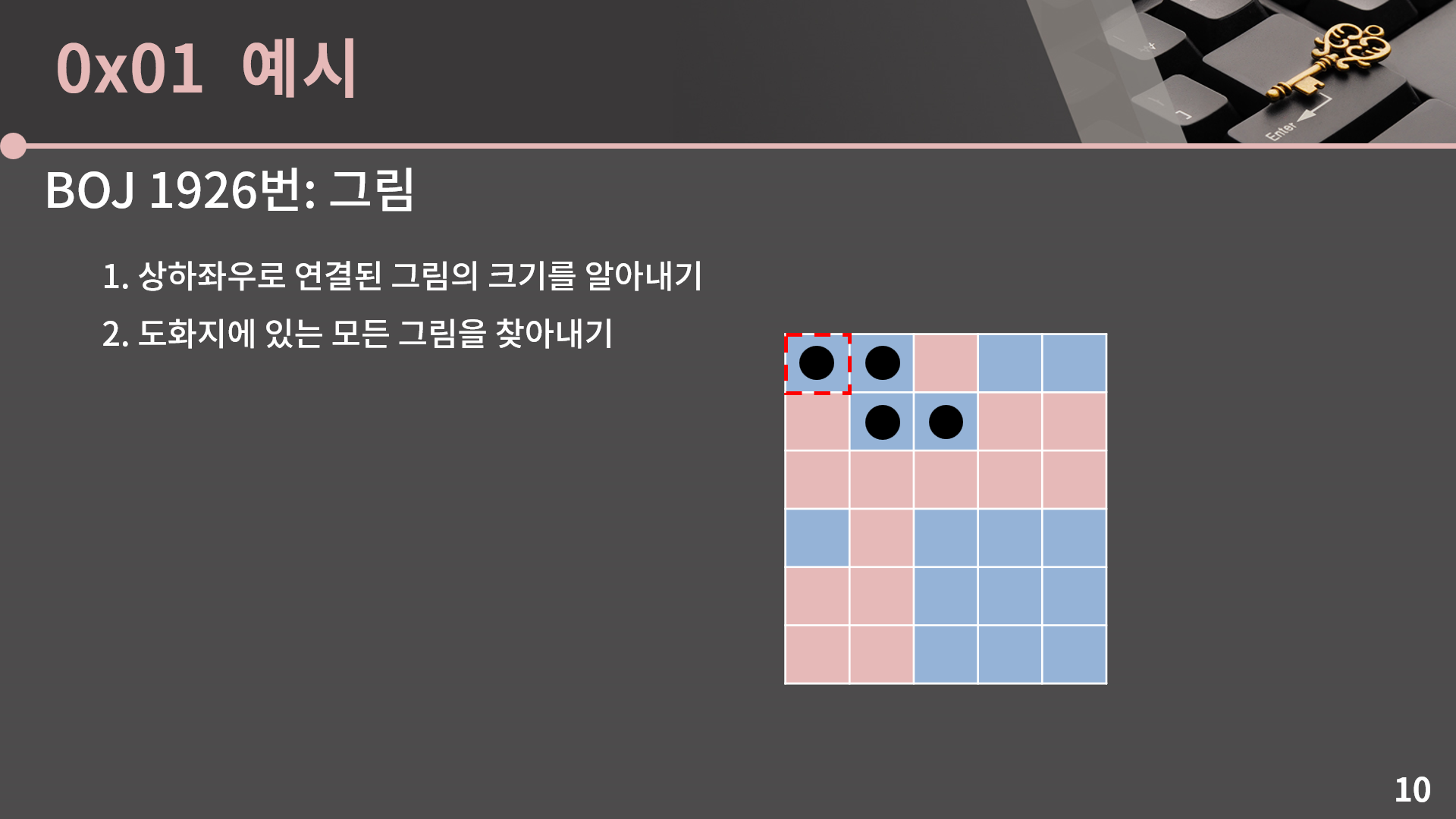
일단 (0, 0)는 파란 칸이고 아직 방문을 안했으니 여기서 BFS를 시작하면 크기가 4인 그림이 찾아질 것입니다. BFS를 돌고 나면 방문 표시도 적절하게 남게 됩니다.
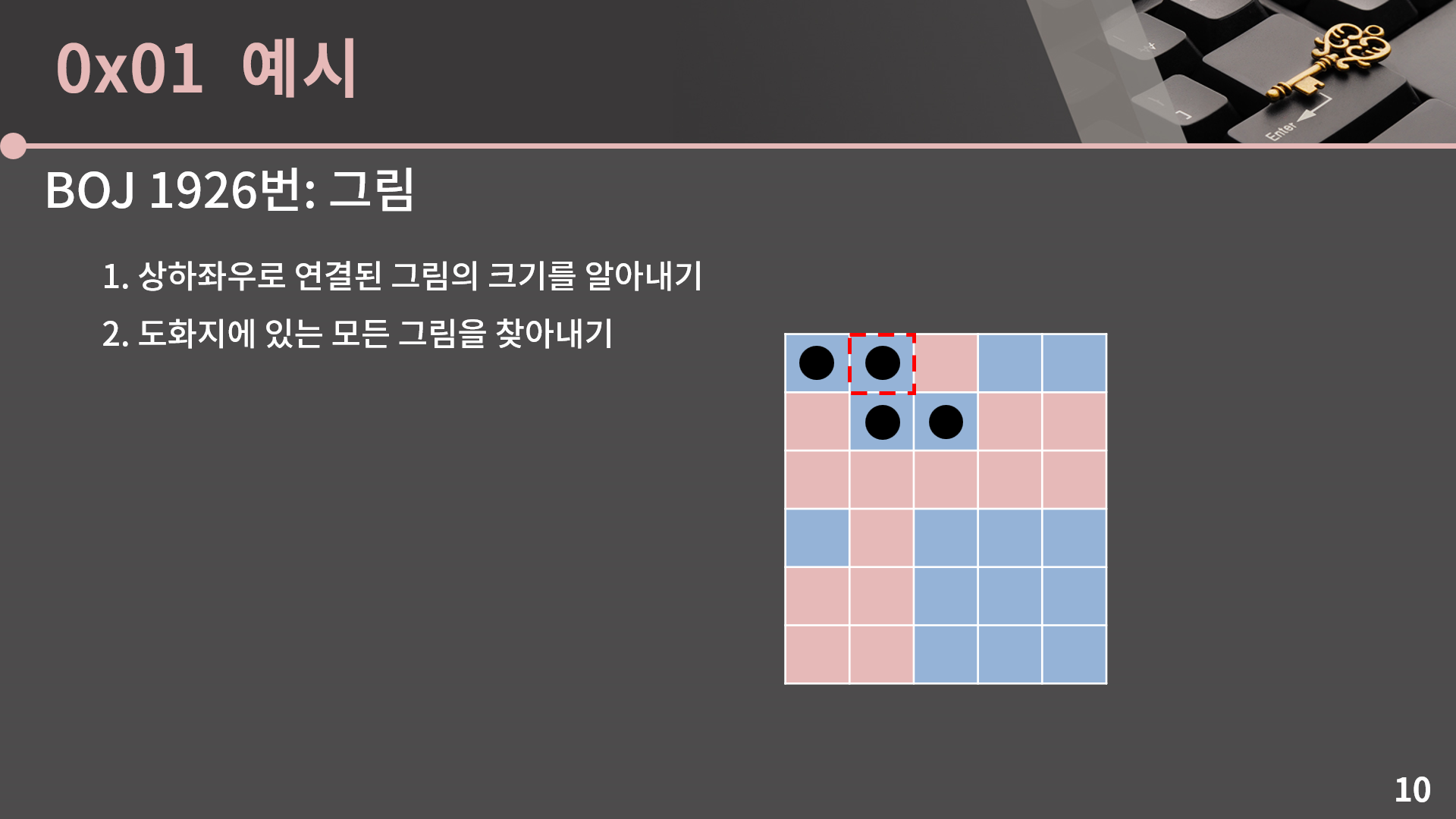
그리고 그 후로 (0, 1)이 시작점이 될 수 있는지보면 (0, 1)은 파란 칸이지만 이미 방문을 했으니 여기서 또 BFS를 돌리면 안되겠죠.

다음에는 (0, 2)인데 여기는 애초에 빨간 칸이니 거릅니다.

그 다음 (0, 3)은 파란 칸이고 아직 방문을 하지 않았으니 새로운 그림입니다. 그렇기 때문에 여기서 BFS를 시작합니다.
이와 같이 이중 for문으로 각 칸이 BFS의 시작점이 될 수 있는지를 체크해주면 도화지에 있는 모든 그림을 찾아낼 수 있습니다. 그리고 여기서도 결국 각 파란 칸은 큐에 딱 한 번씩만 들어가서 시간복잡도는 칸의 갯수만큼만 필요합니다. 이 문제에서는 O(nm)입니다.

방법은 알았으니 구현을 하면 됩니다. 제 코드를 한 번 감상해보시면 앞의 BFS 코드에서 조금만 변형한걸 알 수 있습니다. 천천히 코드를 분석해보면 말한대로 이중 for문을 돌면서 (i, j)가 BFS의 시작점이 될 수 있는지 확인합니다. 빨간 칸이거나 이미 방문했으면 제외하고, 이후 그 점을 시작점으로 BFS를 돌립니다.
그리고 while문 안에서 pop이 이루어질 때 마다 area값을 1 증가시키면 area의 값이 곧 그림의 넓이가 됩니다. BFS의 과정을 잘 이해하고 있다면 이 정도의 응용은 따라가는데 큰 무리가 없을 것 같은데, 아직 조금 아리까리하다면 과정을 계속 들여다보면서 확실하게 이해할 필요가 있어보입니다. (코드 링크)

BFS로 Flood Fill을 수행하는 것을 같이 살펴봤는데, Flood Fill 말고도 정말 다양한 응용이 있고, 안타깝게도 BFS는 코딩테스트 단골 문제이기 때문에 이런 응용들을 모두 잘 알고 있어야합니다. 그 응용 중에서 첫 번째로 다차원 배열에서의 거리 측정을 보겠습니다. BOJ 2178번 미로 탐색 문제를 확인해봅시다.
문제를 보시면 이 문제는 미로의 좌측 상단으로부터 우측 하단으로 가는 최단 경로의 길이를 찾는 문제입니다. 그리고 BFS를 이용해 시작점에서 연결된 다른 모든 점으로의 최단 경로를 찾을 수 있습니다.
이 성질을 이해하기 위해 BFS의 과정을 다시 살펴보겠습니다. 지금 상황은 (0, 0)에서 BFS를 도는 상황인데, 뭔가 (0, 0)에서 사방으로 퍼져나가는 것과 같은 느낌이 들지 않나요? 감이 잘 안온다면 다음 슬라이드를 같이 보겠습니다.

이번에는 방문했다는 표시 대신에 각 칸들에 (0, 0)까지의 거리를 적어놨는데 눈에 들어오는게 있나요? 보면 빨간색 칸은 현재 보는 칸이고 검정색은 추가되는 칸인데, 현재 보고 있는 칸으로부터 추가되는 인접한 칸은 거리가 현재 보는 칸보다 1만큼 더 떨어져 있습니다.
제일 첫 번째는 빨간색 칸에서 거리가 0인데 검정색 칸에서 거리가 1이고, 마지막껀 빨간색 칸에서 거리가 4인데 검정색 칸에서는 거리가 5입니다. 이 성질을 활용하면 우리는 단순히 상하좌우로 연결된 칸들을 방문하는 것에서 끝나는 것이 아니라, 시작점과의 거리를 전부 계산할 수 있습니다.
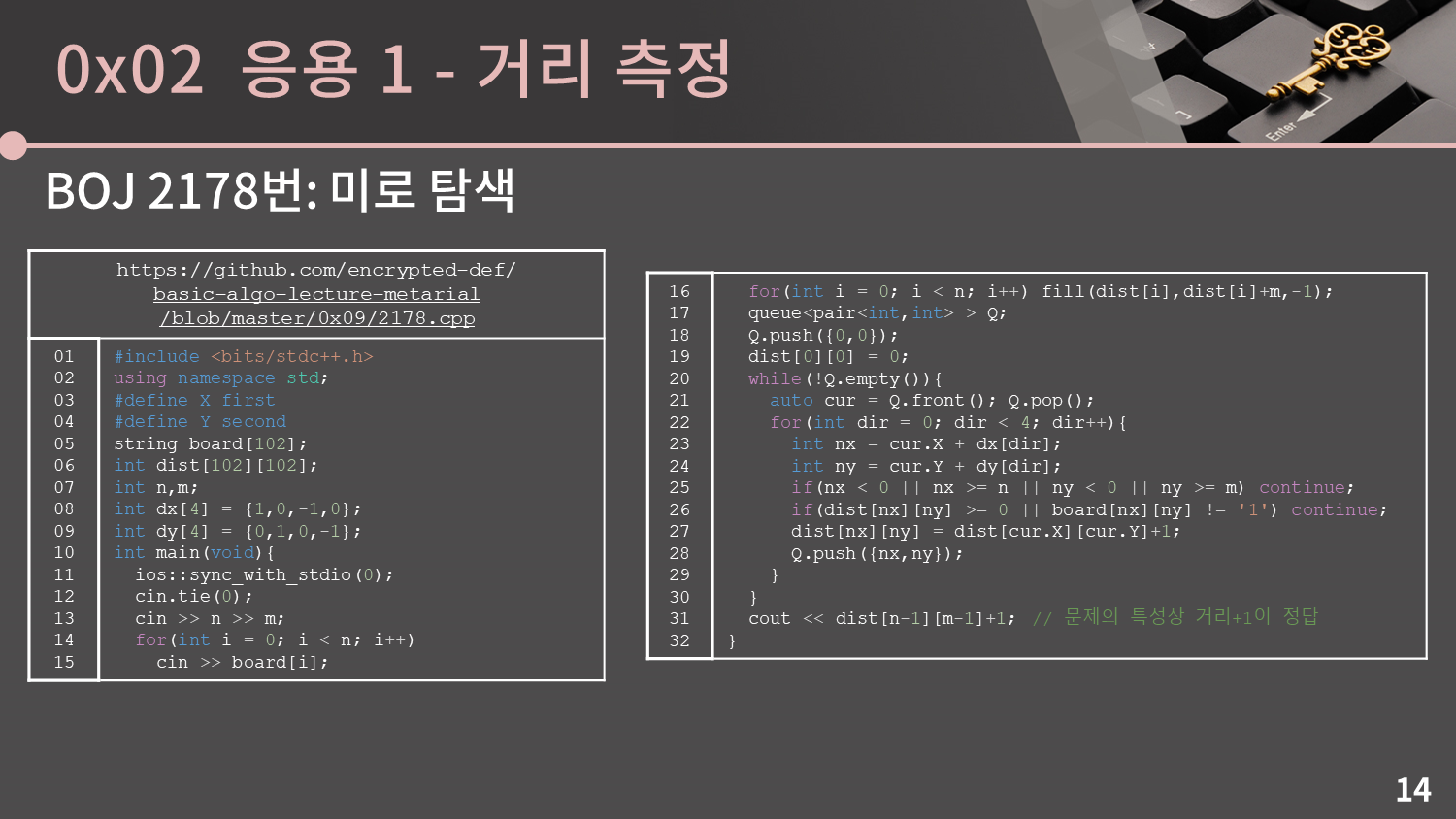
구현의 흐름은 일반적인 BFS와 크게 다르지 않습니다. 거리를 저장할 dist 배열을 두고 상하좌우의 칸을 볼 때 값을 잘 넣어주면 됩니다. 그리고 이 배열을 미리 -1로 초기화해두면 굳이 vis 배열을 따로 두지 않아도 방문 여부를 확인할 수 있게 됩니다.
구현한 코드를 같이 봅시다. 일단 입력을 string 배열에 받았고 dist 배열은 전부 -1로 초기화시켜뒀습니다. 초기화를 할 때 fill을 썼는데 잘 이해가 안가면 0x03강을 참고하셔도 좋고, 그냥 fill 대신 이중 for문을 돌면서 -1을 대입해도 아무 상관 없습니다. 그리고 큐 안에서 도는 과정은 vis 대신 dist를 썼다는 것만 차이가 있고 크게 달라진게 없어서 이해에 큰 무리가 없을 것 같습니다.

BFS로 거리를 잴 수 있는 것도 알았으니 다음 응용으로 넘어가겠습니다. BOJ 7576번 토마토 문제를 확인하고 옵시다. 일단 이 문제가 BFS라는걸 보고 캐치하실 수 있으셨는지 궁금합니다. 토마토가 익어가는 상황 자체가 BFS를 하는 것과 똑같기도 하고, 토마토가 다 익기까지 필요한 최소 일수를 구하려면 모든 익지 않은 토마토들에 대해 가장 가깝게 위치한 익은 토마토까지의 거리를 구해야한다는 관점에서 살펴봐도 마찬가지로 BFS를 활용할 수 있겠다는 생각이 들 것입니다.
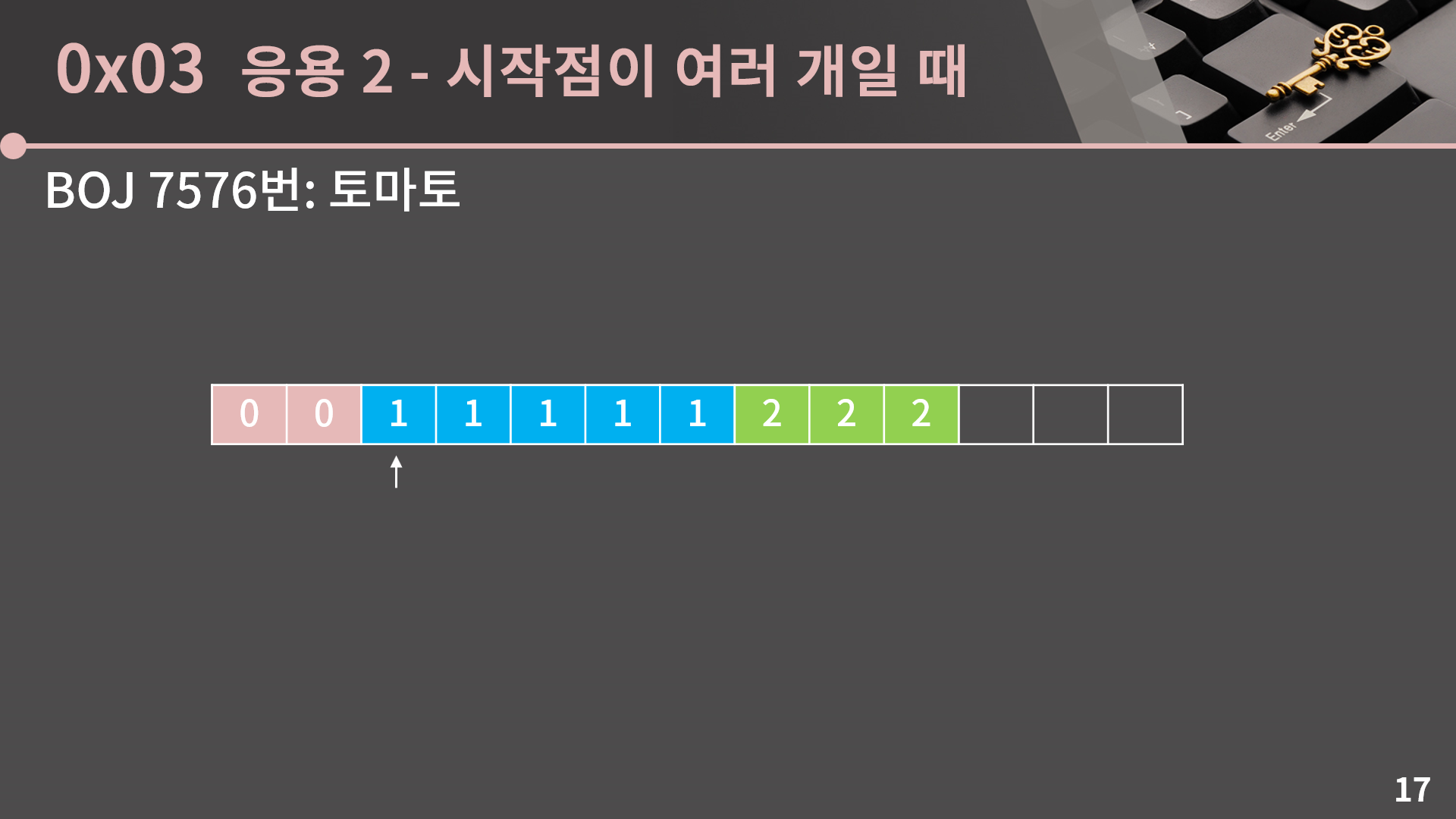
그래서 만약 익은 토마토가 1개였다면 앞의 미로 탐색 문제랑 비슷하게 익은 토마토가 있는 곳을 시작점으로 해서 BFS를 돌려 쉽게 해결이 가능할텐데 이 문제에서는 익은 토마토의 갯수가 여러 개일 수 있습니다. 각 익은 토마토들에 대해 해당 위치를 시작점으로 하는 BFS를 한 번씩 다 돌리는 방법을 떠올릴 수 있지만, 그러면 BFS의 시간복잡도가 O(NM)이고 익은 토마토 또한 최대 NM개가 있을 수 있으니 총 O(N2M2)이 되어 시간 내로 해결이 안될 것입니다. 과연 어떻게 문제를 해결할 수 있을까요?
지금까지의 상황을 다시 정리해보면 우리는 지금 시작점이 여러 개인 BFS를 돌 수 있어야합니다. 그리고 해결법은 의외로 간단한데, 그냥 모든 시작점을 큐에 넣고 앞에서 한 것과 똑같이 BFS를 돌면 끝입니다. 지금 슬라이드에서의 그림을 보면 파란색은 익지 않은 토마토, 초록색은 익은 토마토, 빨간색은 빈 칸을 의미합니다. 현재 익은 토마토가 2개가 있는데, 그 2개를 큐에 넣어두고 BFS를 돌리면 이렇게 자연스럽게 거리가 잘 구해지게 됩니다.

코드를 한 번 보겠습니다. 일단 입력을 받으면서 익은 토마토는 큐에 넣고, 익지 않은 토마토는 dist 값을 -1로 둡니다. 노파심에 말을 드리는데 전역 변수로 잡은 int나 int 배열은 따로 초기화를 안하면 0이 채워지니 익은 토마토가 들어있거나 빈 칸인 곳은 dist 값이 0인 것을 인지하고 코드를 확인하셔야 합니다.
이후 BFS를 도는 부분은 크게 특이한 점이 없고, 마지막에 답을 출력할 땐 거리가 가장 먼 것을 찾지만 익지 않은 토마토가 있는지를 꼭 확인해줘야 합니다. 이렇게 토마토 문제를 처리할 수 있습니다. 참고로 BOJ 7569번: 토마토 문제는 거의 똑같은데 3차원입니다.
3차원이라고 해서 크게 다를건 없고, 단지 배열이 3차원이고 6개의 인접한 칸을 처리하기 위해 dx, dy, dz가 필요하게 됩니다. 이 문제는 여러분에게 맡기겠습니다. 구현할 때 STL tuple이라고 하는 것을 이용하면 좋습니다.

그리고 이 문제를 풀 때에는 쓰이지 않았지만 알아둘 필요가 있는 BFS의 성질이 하나 더 있는데, 앞의 코드가 어떤 식으로 동작하는지 같이 생각해보겠습니다.
문제에서의 표현은 익은 토마토와 익지 않은 토마토이긴 한데, 그냥 여러 개의 시작점에서 모든 지점으로의 거리를 구하는 문제라는 것을 우리는 알고 있습니다.

코드를 다시 떠올려보면 일단 익은 토마토, 즉 거리가 0인 칸들을 큐에 다 넣습니다.

이 때 첫 번째 칸을 통해 추가되는 칸은 앞에서 같이 본 성질로 인해 거리가 1입니다.

그 다음 칸을 통해 추가되는 칸들도 마찬가지로 거리가 1입니다.
이제 거리가 0인 칸들은 큐에서 다 빠졌고, 순차적으로 1인 칸들을 pop할텐데 잘 생각해보면 1인 칸들을 pop하는 동안 거리가 2인 칸들이 쭉 추가될 것입니다.

거리가 1인 칸들이 다 빠지고 2인 칸들을 볼 때면 3인 칸들이 쭉 추가될 것입니다. 이제 전체적인 큐의 모양을 확인해보시면 이와 같이 BFS를 돌 때 큐에 쌓이는 순서는 반드시 거리 순이게 됩니다.
이제 응용 4개 중에 절반을 끝냈습니다. 마저 화이팅합시다. BOJ 4179번 불! 문제를 확인합시다. 확인해보면 아마 굉장히 막막할 것 같은데 그래도 BFS 파트에 소개했다는건 BFS로 풀 수 있다는 얘기일테니, 한 번 고민을 해봅시다.
지금까지 배운 내용을 잘 이해했다면 불의 전파를 BFS로 처리할 수 있음을 알 수 있을 것입니다. 그런데 지금은 지훈이의 탈출도 같이 처리를 해주어야 하고, 이게 꽤 어렵습니다. 일단 결론적으로 말해 이런 문제는 불에 대한 BFS와 지훈이에 대한 BFS를 모두 돌림으로서 해결이 가능합니다.
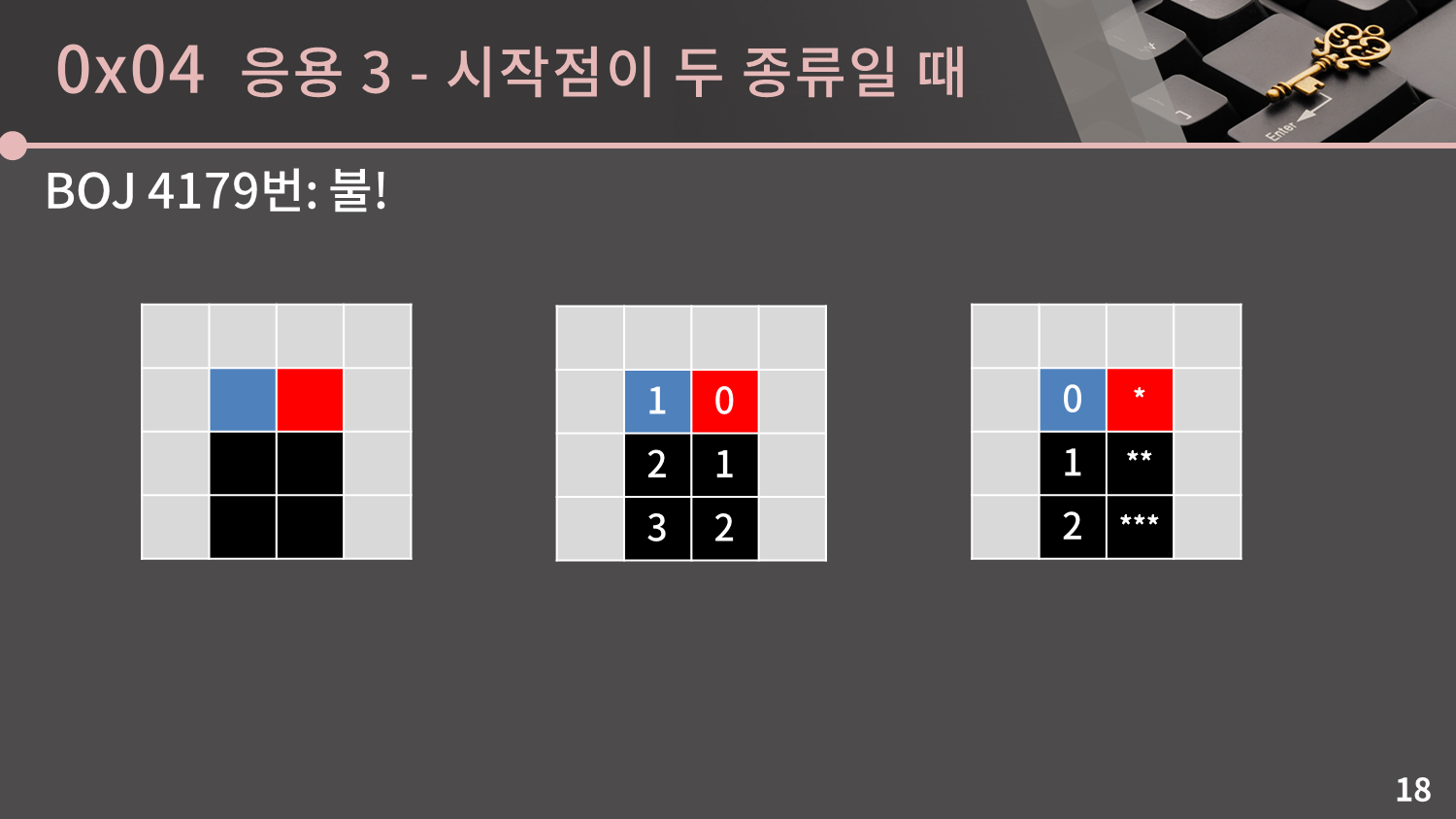
먼저 지훈이는 신경쓰지 말고 불에 대한 BFS를 돌려서 미리 각 칸에 불이 전파되는 시간을 다 구해둡니다. 두 번째의 맵이 바로 각 칸에 불이 전파시간을 의미합니다.
그 다음에는 지훈이에 대한 BFS를 돌리며 지훈이를 이동시킵니다. 이 때 만약 지훈이가 특정 칸을 x시간에 최초로 방문할 수 있는데 그 칸에는 x시간이나 그 이전에 불이 붙는다면 그 칸을 못가게 됩니다.
예를 들어 **으로 마킹한 칸을 보면 지훈이는 저 칸에 2시간이 될 때 방문하게 됩니다. 그런데 불은 이미 1시간만에 전파되었기 때문에 지훈이는 저 곳을 갈 수 없습니다. *, ***으로 마킹한 칸도 마찬가지 이유로 지훈이가 갈 수 없는 칸입니다.
원래 BFS의 구현에서는 큐 안에서 (nx, ny)를 살펴볼때 방문했는지 여부를 vis[nx][ny]가 true인지 혹은 dist[nx][ny]가 0 이상인지 확인하고, 이미 방문한 칸이라면 continue를 합니다. 이 문제에서는 추가로 해당 칸에 불이 붙은 시간을 확인해서 필요에 따라 continue를 하면 됩니다. 이렇게 BFS와 지훈이에 대한 BFS를 따로 해서 문제를 그렇게 어렵지는 않게 해결할 수 있습니다.
지금 이 방식을 토대로 구현해보는 시간을 가져보도록 하겠습니다. 한 번 시도해봅시다.

지금까지 같이 배운 것을 토대로 구현을 하면 어렵긴 해도 못할 난이도는 아닐 것 같은데 어떤지 모르겠습니다. 일단 제 코드를 같이 보겠습니다.
이 문제의 코드는 도저히 한 슬라이드에 다 담을 수가 없었습니다. 한 20줄 정도가 더 남아있는데 일단 지금 여기까지를 한 번 보겠습니다. 불에 대한 BFS는 Q1, dist1을 활용하고 지훈이에 대한 BFS는 Q2, dist2를 활용할 것입니다. 불에 대한 BFS는 늘 해오던 것과 똑같습니다.

불에 대한 BFS가 끝나고 나면 dist1에는 해당 지점에 불이 언제 붙는지가 저장됩니다. 그 다음으로는 지훈이에 대한 BFS를 돌면서 외곽으로 빠져나올 수 있게 해야하는데 지금까지의 BFS에서는 목적지가 정해져있거나 더 이상 갈 곳이 없을 때 까지 계속 돌리는 상황이었던 반면 이번에는 외곽으로 탈출을 해야하니 52번째 줄의 처리가 들어가게 됩니다. 주석으로 적어놓은 것 처럼 (nx, ny)가 범위를 벗어났다는건 곧 탈출에 성공했다는 의미이고, 17번 슬라이드에서 본 것과 같이 큐에 원소들은 거리 순으로 들어가니 최초로 탈출한 시간을 바로 출력하고 종료하면 됩니다.
그리고 지훈이는 자신이 도착한 시간과 동시에 불이 도착하거나, 혹은 자신보다 더 빨리 불이 도착하는 자리로는 갈 수 없기 때문에 58번째 줄의 조건이 추가로 들어가게 됩니다. 만약 프로그램이 종료되지 않고 while문이 끝나게 된다면 지훈이가 탈출에 실패했다는 의미이니 IMPOSSIBLE을 출력하면 됩니다.
이렇게 시작점이 두 종류인 문제를 해결할 수 있게 됩니다. 그런데 시작점이 두 종류인 문제에 관해서 저희가 생각해야 할 점이 사실 추가로 있습니다. 지금 이 방식이 가지고 있는 문제는 무엇인가 하면, 지금은 지훈이의 이동은 불의 전파에 영향을 받지만 불의 전파는 지훈이의 이동에 영향을 받지 않아서 불만 먼저 전파를 쭉 시키는게 가능했습니다. 그런데 예를 들어 시작점이 A, B 두 종류가 있고, A의 전파에 B가 영향을 주고 B의 전파에도 A가 영향을 준다고 해봅시다. 지금 이 문제에서 불과 지훈이가 아니라 불과 소방수 내지는 불과 물이 전파되는 문제여서 둘이 만나면 뭔가 상호작용이 발생한다고 생각을 하는거죠.
그런 상황을 생각해보면 어느 하나를 먼저 끝까지 전파시키는게 불가능합니다. 제가 출제했던 18809번 문제가 딱 그런 문제입니다. 아쉽게도 이 문제는 백트래킹 기법을 추가로 알고 있어야 해결이 가능하기 때문에 당장 풀어볼 수는 없지만, 두 종류의 BFS에서 BFS를 돌 때 어느 하나가 독립적이지 않고 서로에게 영향을 준다면 지금 보여드린 방법으로는 해결할 수 없다는 것을 꼭 이해하셔야 합니다. 그런 상황에서는 시간 순으로 A와 B를 동시에 진행시켜야 합니다.
이 부분은 충분히 생각해볼 가치가 있고, 두 종류의 시작점 문제를 몇 개 풀다보면 지금 제가 한 얘기가 더 명확하게 이해가 갈 것입니다. 그 때 다른 사람의 코드를 찾아보거나 직접 고민하면서 시간 순으로 A와 B를 동시에 진행시킨다는 의미를 이해해보면 좋겠습니다.

드디어 마지막 BFS입니다. 정말 감개무량합니다. BOJ 1697번 숨바꼭질 문제를 한 번 보고 오시면 지금까지 다뤘던 문제들이랑은 느낌이 많이 다른 것을 확인할 수 있습니다. 지금까지는 죄다 2차원 배열 형태에서 상하좌우로 움직이는 모양새였는데 얘는 전혀 다릅니다. 그래서 이게 BFS랑 관계가 있긴 한건가 싶을텐데, 이 문제도 BFS입니다.

이차원에서의 BFS를 생각하면 지금 이 그림처럼 현재 선택된 칸에서 상하좌우로 뻗어나가는 방식으로 진행이 됐습니다. 왜 상하좌우로 뻗어갔나 생각해보면 그게 불이 됐든 토마토가 됐든 전파가 상하좌우로 이루어졌기 때문입니다.
그럼 약간의 창의성을 발휘해서 아래와 같이 이 문제에서도 수빈이가 X에 있다고 할 때 X-1, X+1, 2X로 이동하는 것을 BFS로 처리할 수 있겠다는 생각을 해볼 수 있습니다.
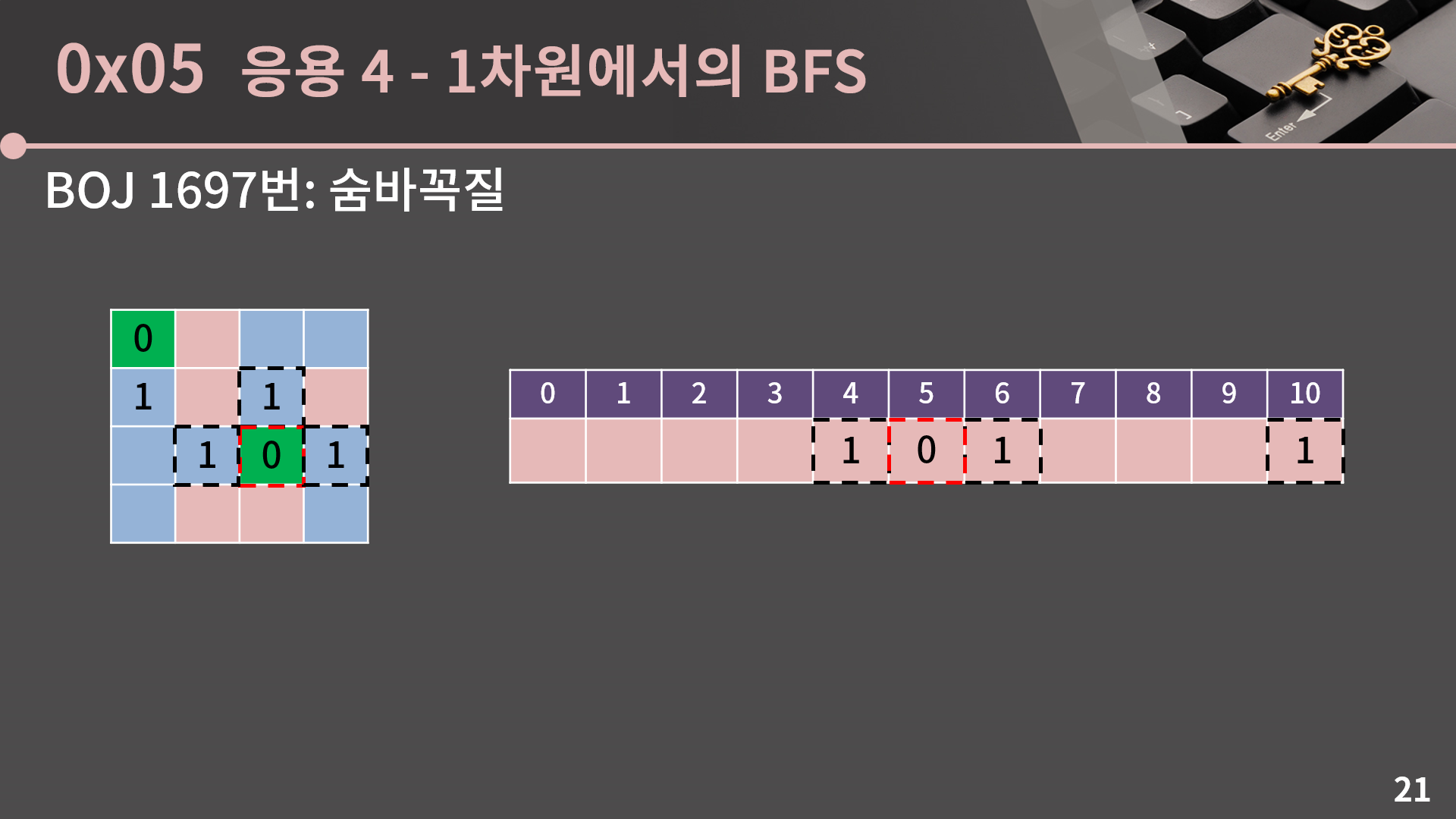
수빈이가 예제처럼 5에 있었다고 치면 5에서 BFS를 시작하고, 5에서 갈 수 있는 4, 6, 10은 거리가 1이 되는 것입니다.
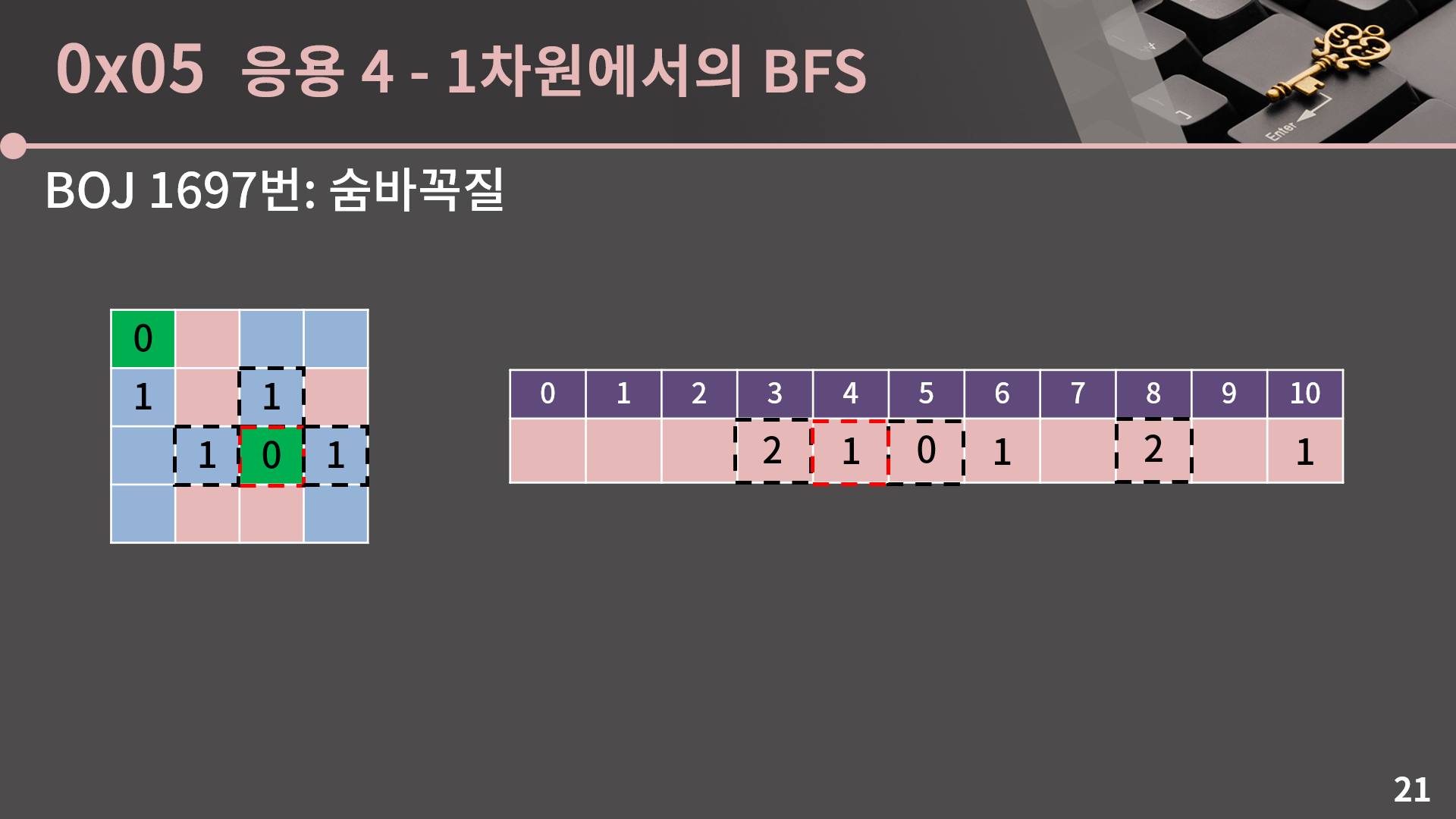
BFS는 이제 충분히 익숙해지셨을 것 같아서 큐는 안그려놨는데, 아무튼 그 다음으로는 4가 선택되고 3, 5, 8을 보는데 5는 이미 값이 써져있으니 3, 8만 거리가 2가 될 것입니다. 이렇게 BFS를 돌다가 동생이 있는 위치의 값이 써지게 되면 문제에서 원하는 답을 알 수 있게 됩니다. 구현이 그렇게 어렵지는 않을 것 같은데 어떤가요? 앞의 문제보다 더 쉬울 것 같습니다.
그런데 사실 한 가지 더 고민해야 할 문제가 있는데, BFS의 범위를 어디까지로 해야할까요? 0부터 100,000으로 하면 되는거 아닌가하고 쉽게 생각을 하셨을수도 있는데, 문제를 보시면 수빈이와 동생의 위치가 0에서 100,000 사이라고 했지 수빈이가 이동 중에 반드시 0에서 100,000 사이에만 있어야한다는 조건은 없습니다. 예를 들어 100,000 밖으로 나갔다가 다시 안으로 올 수도 있습니다. 그래서 이 부분을 고려할 필요가 있습니다.
일단 상식적으로 생각했을 때 음수로 갈 일은 없을 것입니다. 그건 진짜 절대 가장 빠른 경로가 될 수 없기 때문입니다. 그리고 100,000 바깥으로 나갈 수 있겠지만 일단 한 번 나갔다면 그 이후로는 -1만 계속 하게 됩니다. 그렇기 때문에 동생을 가장 빠르게 찾아나가는 상황에서는 아무리 멀리가도 200,000을 넘어가지는 않습니다.
이러한 생각을 거쳐서 0에서 200,000 사이에서만 BFS를 돌려도 답을 구하는데는 문제가 없음을 알 수 있게 되고, 여기서 더 깊게 생각을 해보면 사실 100,000을 나가는 것 자체가 손해라는 것을 알 수 있습니다. +1로 100,000을 탈출하는건 정말 바보짓이고, x2로 100,000을 탈출하는 상황이 있을 수 있겠다 싶지만, x2를 한 후 -1을 여러번 할 바에야 -1을 먼저 하고 x2를 하는게 더 낫기 때문입니다.
지금 설명이 잘 이해가 가지 않을 수 있습니다. 이해가 가지 않더라도 상관은 없지만 이 문제에서 당연히 수빈이가 0에서 100,000 사이에서만 움직인다고 멋대로 가정을 하고 풀면 안된다는 점은 꼭 짚고 넘어가면 좋겠습니다. 이 문제에서는 운 좋게 논리적으로 생각을 했을 때 수빈이가 0에서 100,000 사이에서만 움직이게 되었지만 다른 문제에서는 멋대로 가정한 것 때문에 말아먹을수도 있습니다.

구현에서 크게 어려울건 없을 것 같습니다. 17번째 줄에서 range-based for를 이용했고, 구현 흐름은 늘 보던 것들의 반복입니다. (코드)

굉장히 빡센 BFS가 마무리됐습니다. Flood Fill로 시작해서 거리 측정, 시작점이 여러 개일 때, 시작점이 두 종류일 때, 1차원에서의 BFS를 모두 다뤘는데, 한 강의에서 다루기에 정말 많은 분량이긴 했습니다. 하지만 이왕 하는거 여러 응용들을 잘 섭렵하시라고 이렇게 준비를 했고, BFS부터는 본격적으로 코딩테스트에 정말 잘 나오는 유형이기 때문에 그룹 내의 문제집을 꼼꼼하게 풀어보고 BFS의 기본 틀 자체도 반복적으로 짜면서 코드의 흐름을 손에 익힐 필요가 있습니다.
그럼 고생 많으셨습니다.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x0C강 - 백트래킹 (114) | 2020.07.06 |
|---|---|
| [실전 알고리즘] 0x0B강 - 재귀 (84) | 2020.06.14 |
| [실전 알고리즘] 0x0A강 - DFS (30) | 2020.05.27 |
| [실전 알고리즘] 0x08강 - 스택의 활용(수식의 괄호 쌍) (37) | 2020.03.20 |
| [실전 알고리즘] 0x07강 - 덱 (39) | 2020.03.14 |
| [실전 알고리즘] 0x06강 - 큐 (14) | 2020.03.11 |