
드디어 01 02 03 이렇게 숫자를 넘어서 0A강에 도달했습니다. 아직 완결까지는 한참 남았지만 아무튼 힘을 내서 계속 잘 해봅시다. 아, 참고로 저번 단원보다는 내용이 많지 않아서 편한 마음으로 들으실 수 있을 것입니다.

보시면 BFS에서는 끝도 없이 많았던 응용 파트가 여기서는 싹 사라진걸 볼 수 있습니다. 왜 그런건지는 천천히 같이 알아가도록 하겠습니다.

일단 DFS의 정의는 다차원 배열에서 각 칸을 방문할 때 깊이를 우선으로 방문하는 알고리즘입니다. 참고로 BFS는 깊이 대신 너비를 우선으로 방문하는 알고리즘이었습니다. 깊이나 너비나 모호한건 매한가지일거니 이번에도 마찬가지로 실제 예시를 보면서 DFS의 과정을 이해해야 할 것 같습니다.

과정을 먼저 소개해보면 뭔가 어디서 본 것 같다는 느낌을 받을텐데, 바로 BFS의 과정에서 딴건 다 똑같고 큐만 스택으로 바뀐 것 뿐입니다. 큐를 쓰면 BFS이고 스택을 쓰면 DFS가 됩니다. 이번에는 DFS로 상하좌우로 나와 인접한 같은 색의 칸을 방문하는 Flood Fill을 해결해보겠습니다.
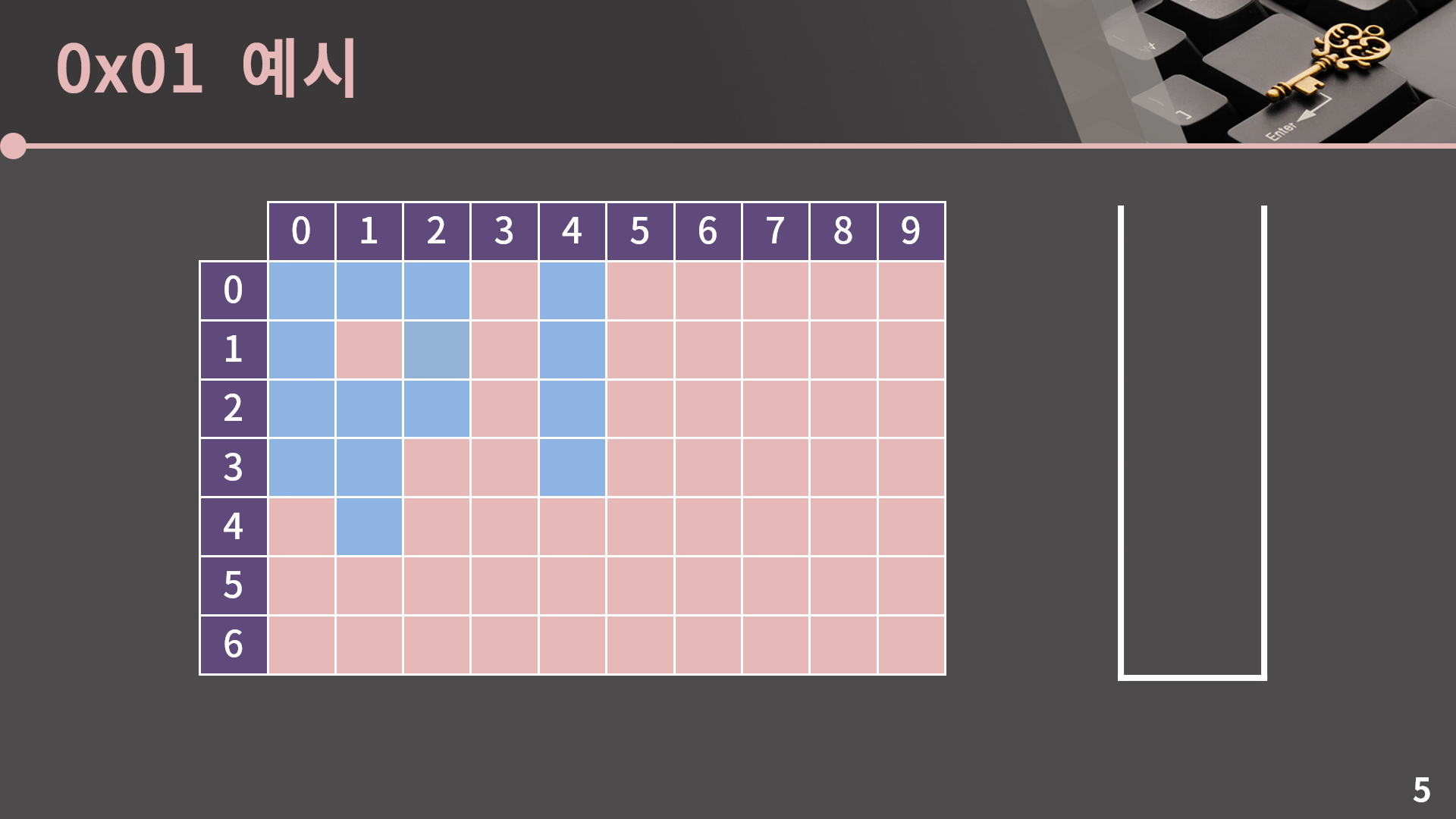
이번에도 (0, 0)과 상하좌우로 이어진 모든 파란색 칸을 확인해보도록 하겠습니다.

우선 (0, 0)에 방문했다는 표시를 남기고 해당 칸을 스택에 넣습니다. 이게 초기세팅이고 이후에는 스택이 빌 때 까지 계속 스택의 top을 빼고 해당 좌표의 상하좌우를 살펴보면서 스택에 넣어주는 작업을 반복하면 됩니다.

지금 스택의 top은 (0, 0)이고 pop을 합니다. 그리고 (0, 0)의 상하좌우 칸을 보는데, 이 중에서 우리는 파란색 칸이면서 아직 방문하지 않은 칸을 찾을 것입니다.

보면 (0, 1)과 (1, 0)이 모두 파란 칸이면서 아직 방문하지 않은 칸이니 방문했다는 표시를 남기고 스택에 넣습니다.

이미 BFS에서 한 번 본 내용이라 더 설명을 안해도 될 것 같긴 하지만 이왕 시작한거 조금만 더 같이 해보겠습니다. 지금 스택의 top은 (1, 0)이고 pop을 하겠습니다. 상하좌우 칸들을 확인해보면 (0, 0)은 파란 칸이지만 이미 방문을 했고, (1, 1)은 빨간 칸입니다. 유일하게 (2, 0)만 파란색 칸이면서 아직 방문하지 않은 칸이니까 (2, 0)에 방문했다는 표시를 남기고 스택에 넣습니다.
이후의 진행은 설명 없이 사진으로 보여드리겠습니다.




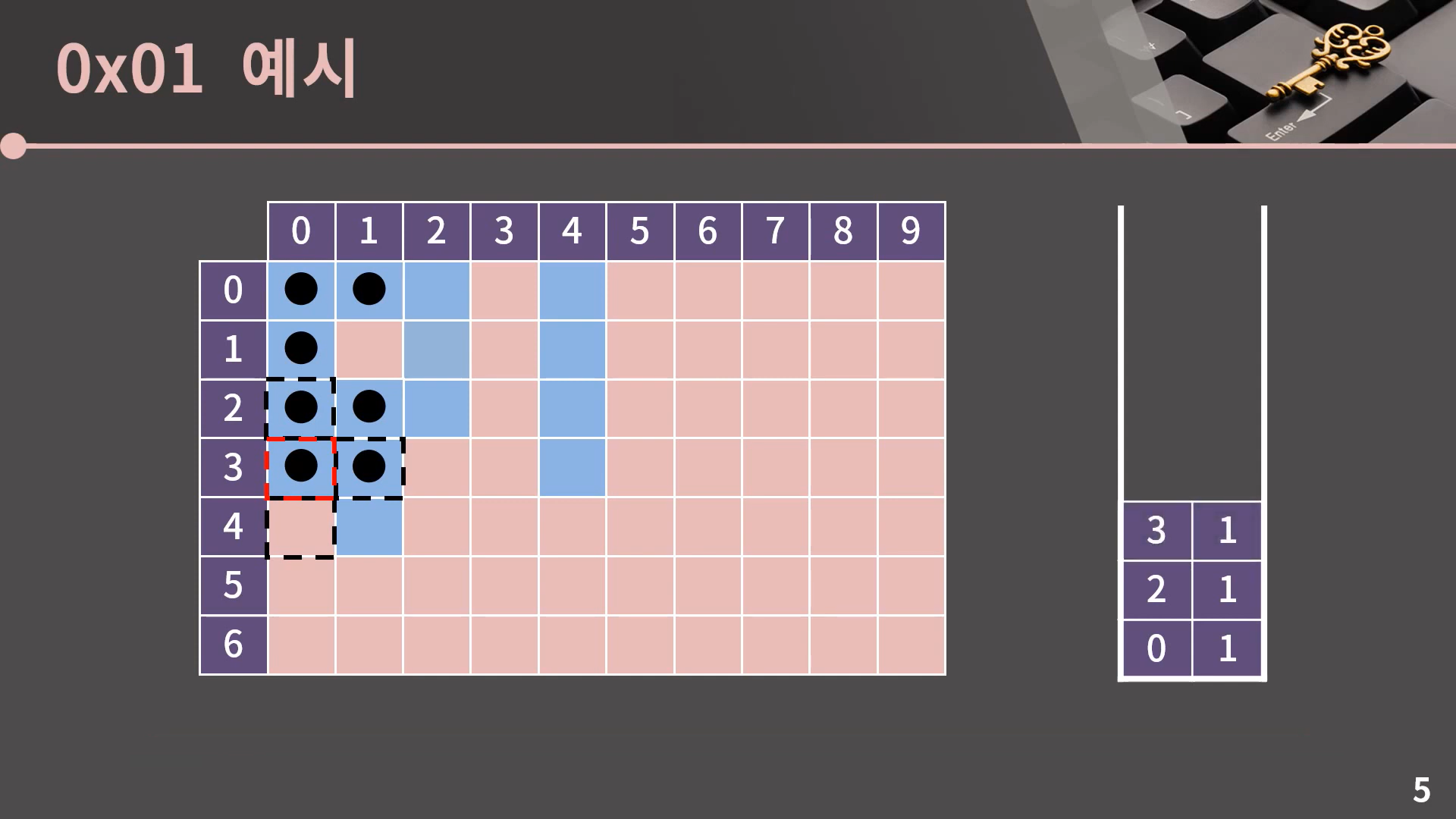
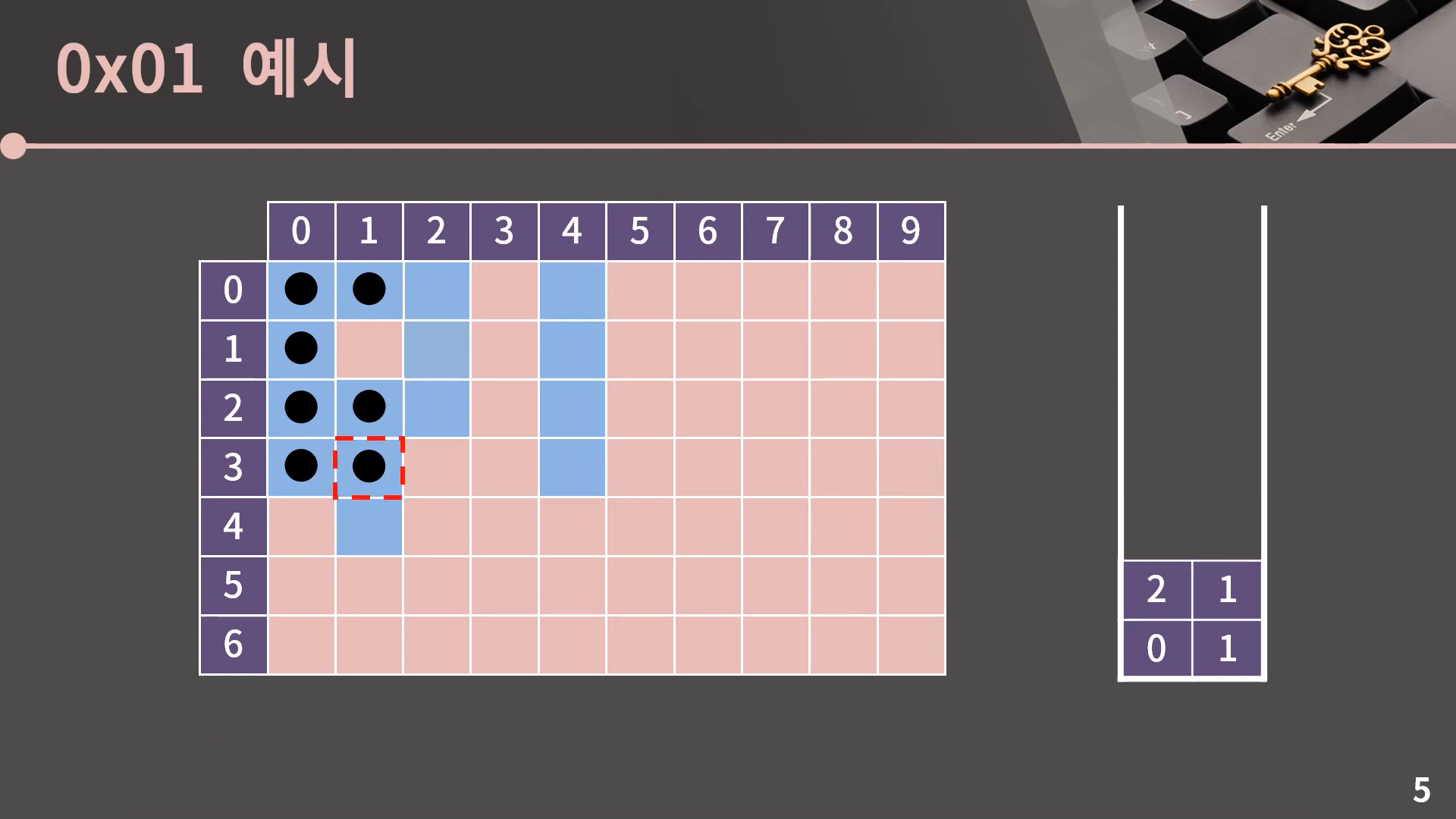
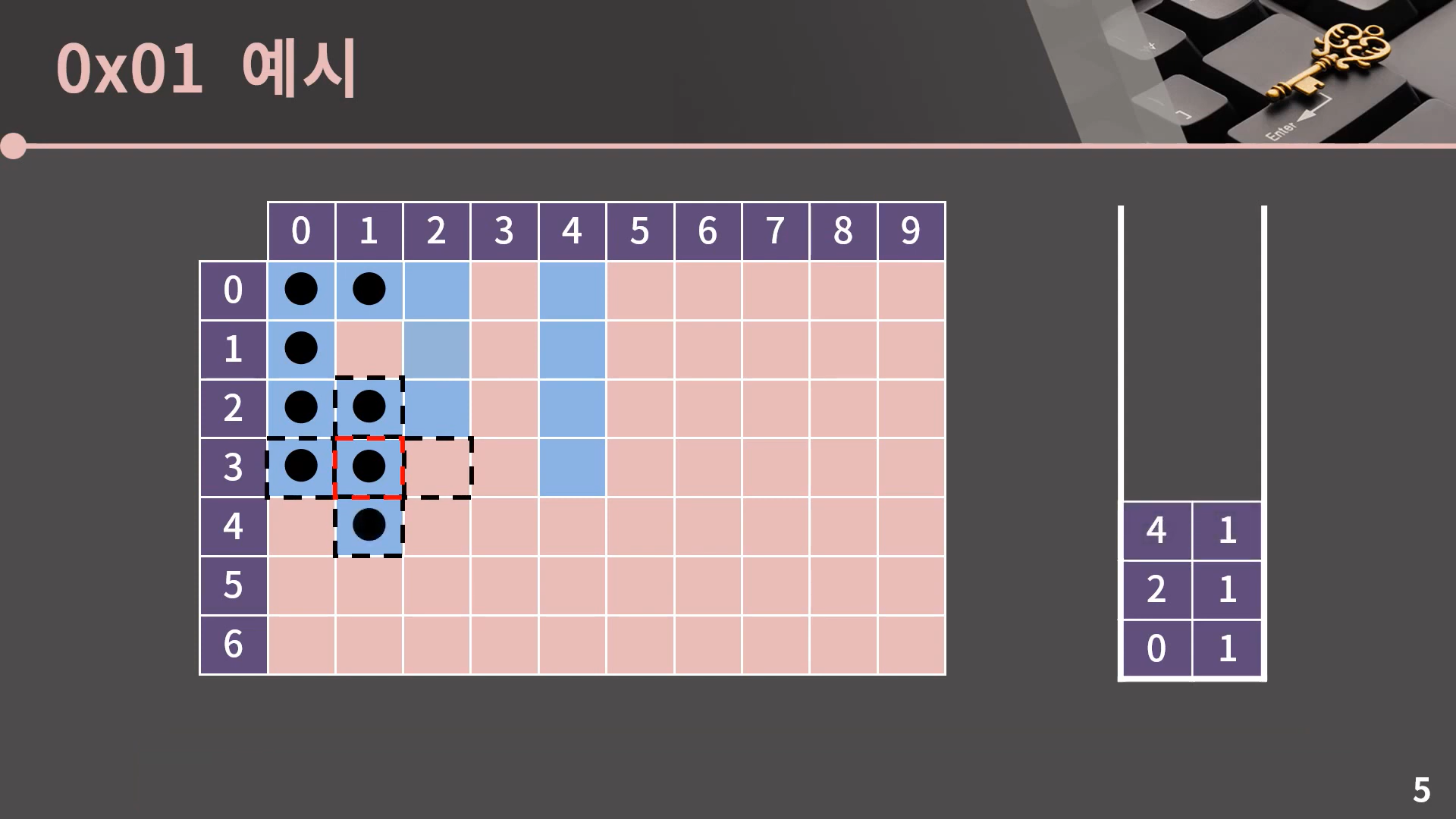
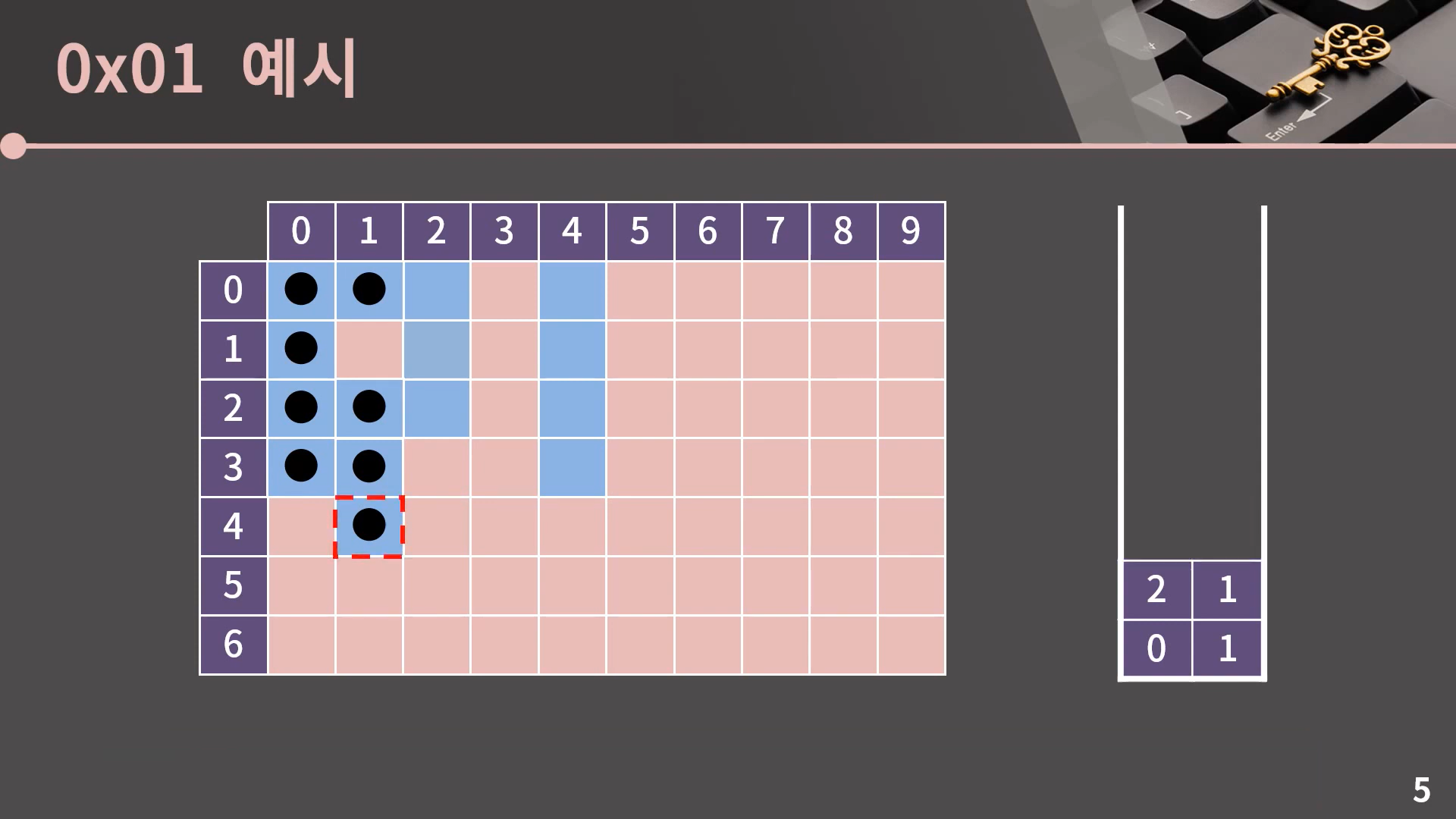

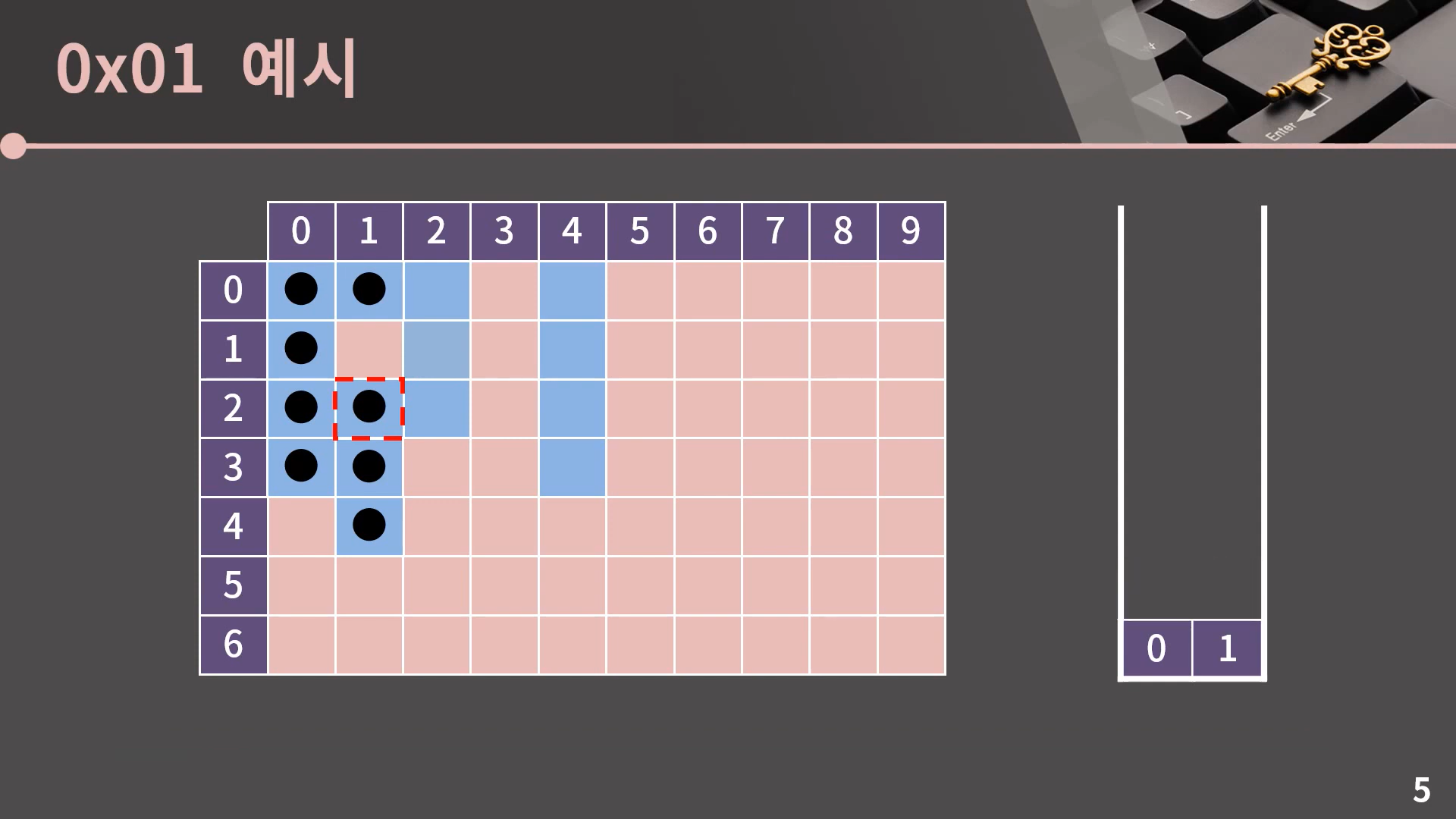


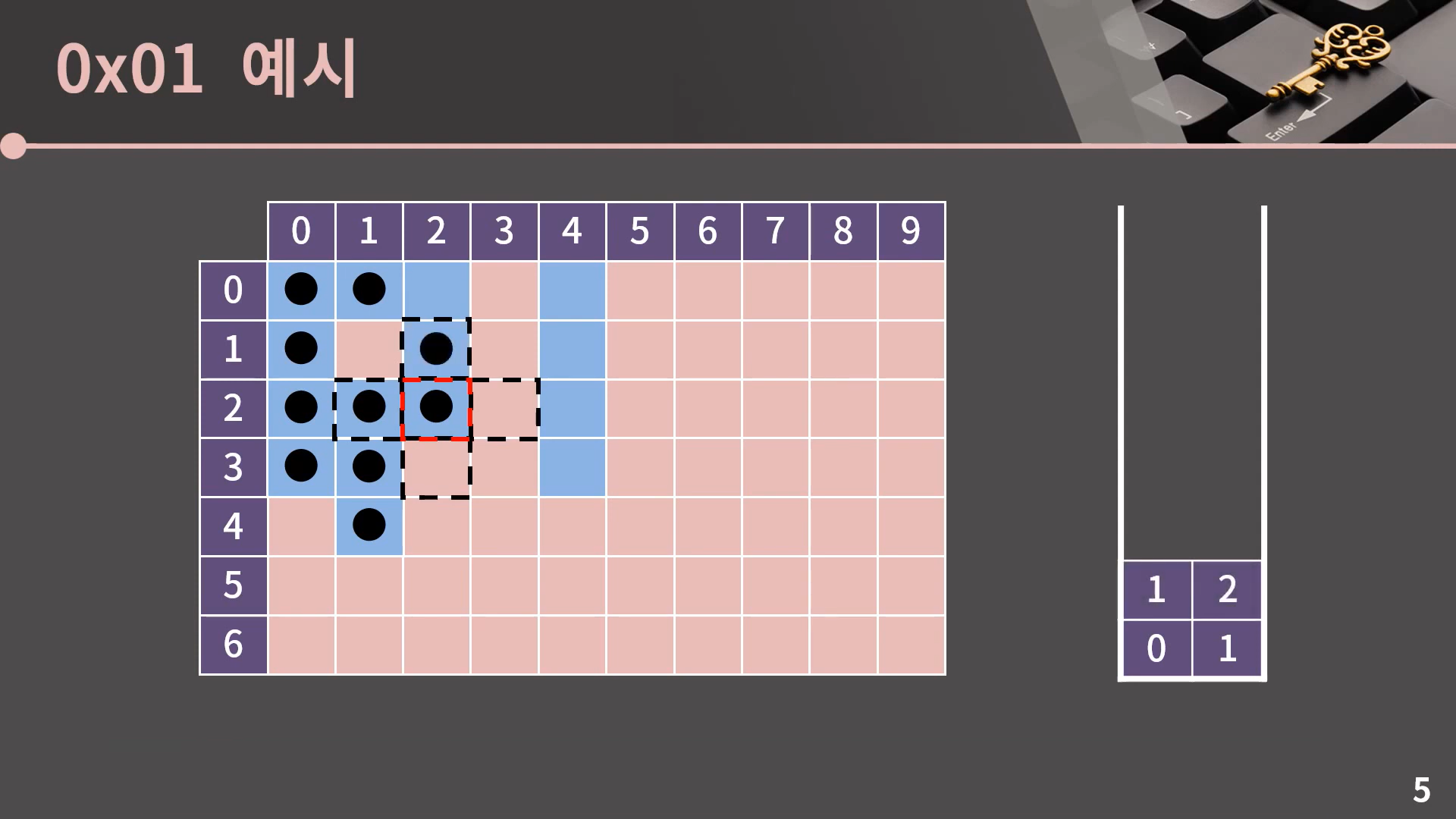

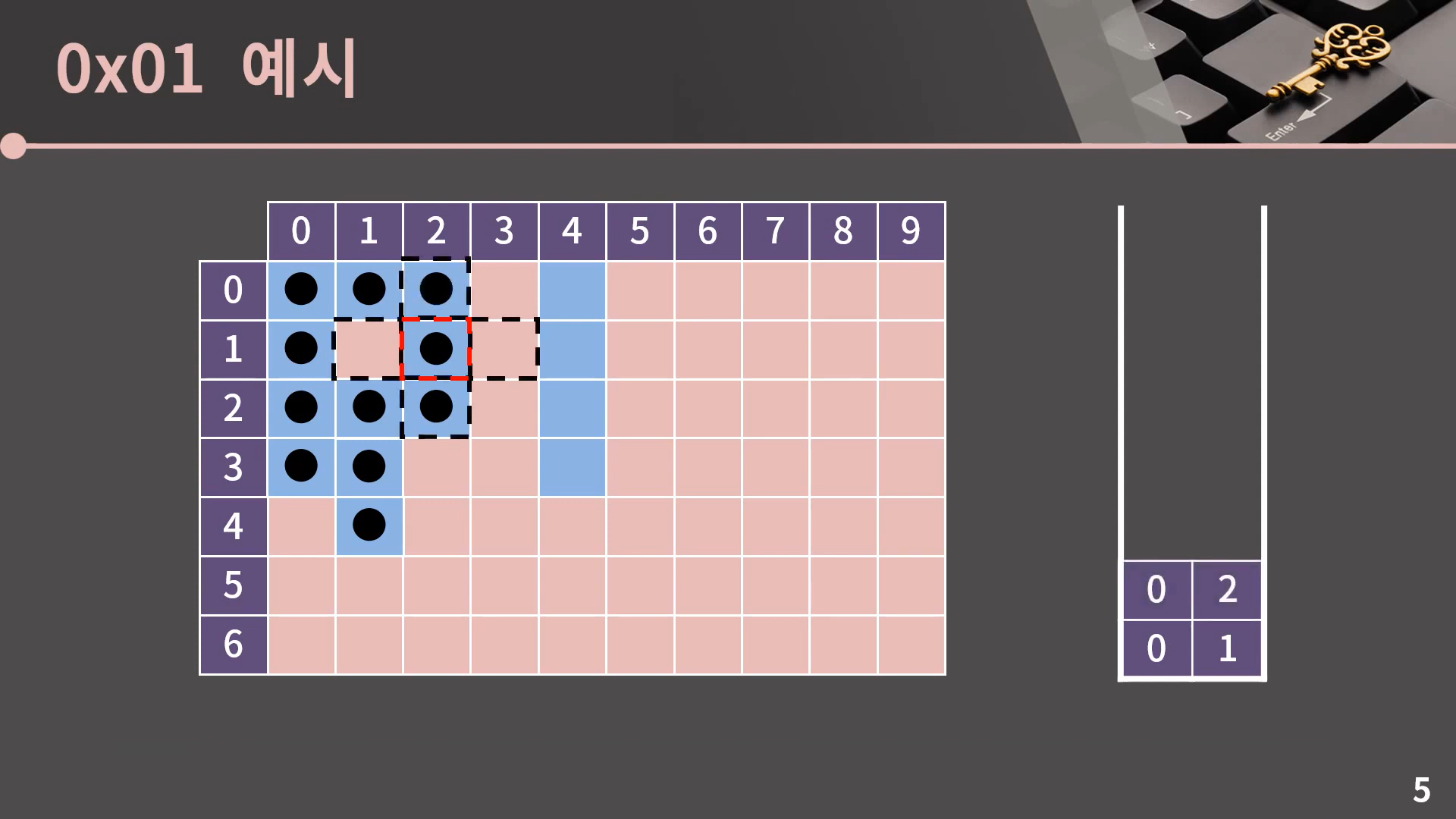




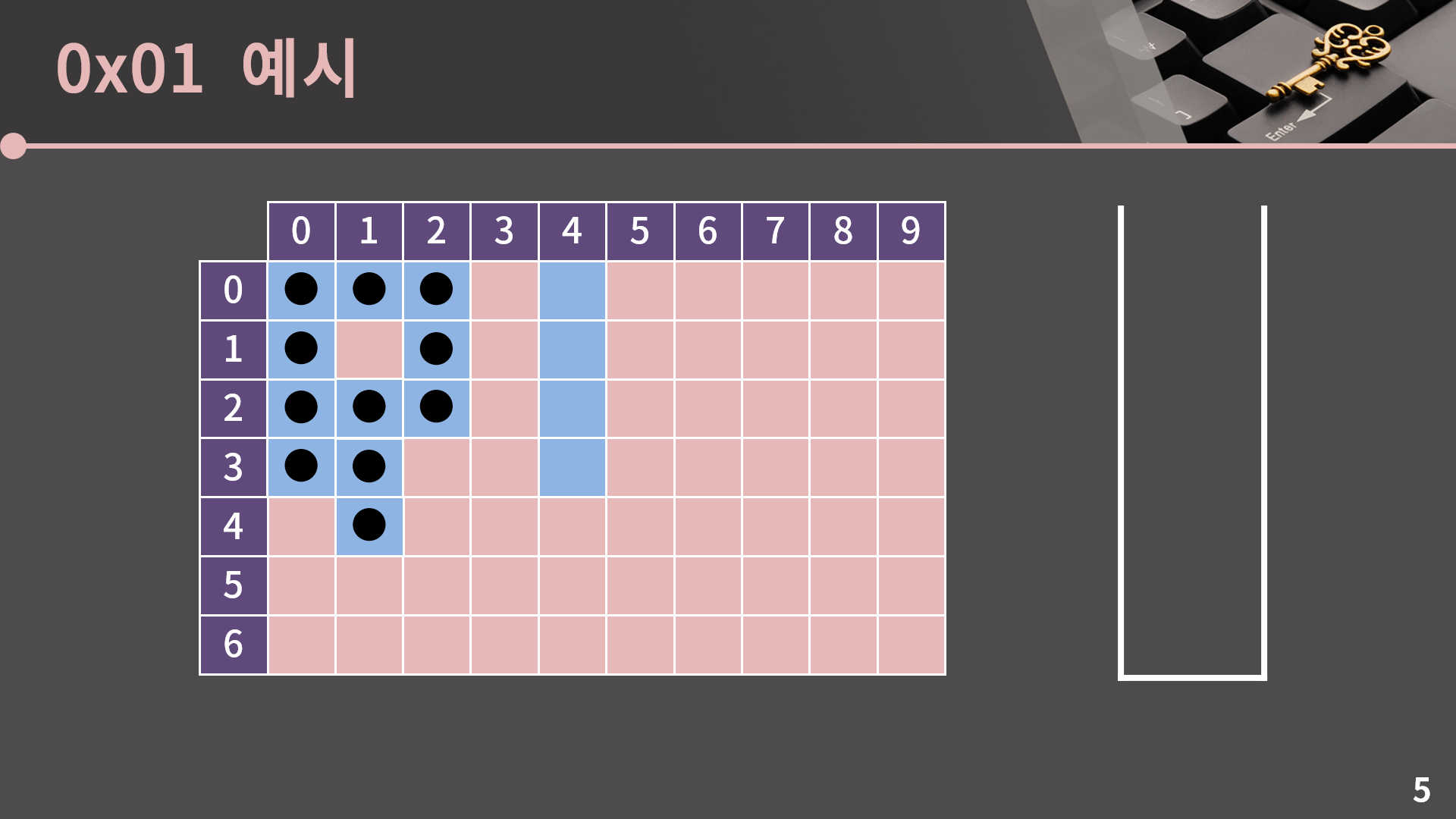
이렇게 스택이 비는 순간 과정은 종료됩니다. DFS도 BFS처럼 Flood Fill이 필요할 때 사용할 수 있음을 알 수 있습니다. 그런데 보면서 느끼셨을지 모르겠지만 BFS와 DFS 모두 비록 최종적인 방문 결과는 똑같더라도 방문 순서에서 아주 큰 차이가 있습니다. 이 부분은 다음 챕터에서 BFS와 DFS를 비교할 때 제대로 설명을 드리겠습니다.

DFS를 구현한 코드를 보면 굉장히 익숙할 것입니다. BFS 코드에서 큐만 스택으로 바꾼 것 뿐입니다. 코드에 대한 설명은 이미 BFS 단원에서 충분히 했기 때문에 여기서 또 하지는 않겠습니다. 이전 단원을 듣지 않고 그냥 DFS를 찾다가 이 강의를 접하게 됐는데 코드에 의문점이 있다면 0x09강 - BFS를 참고하시면 됩니다. (깃헙 링크)
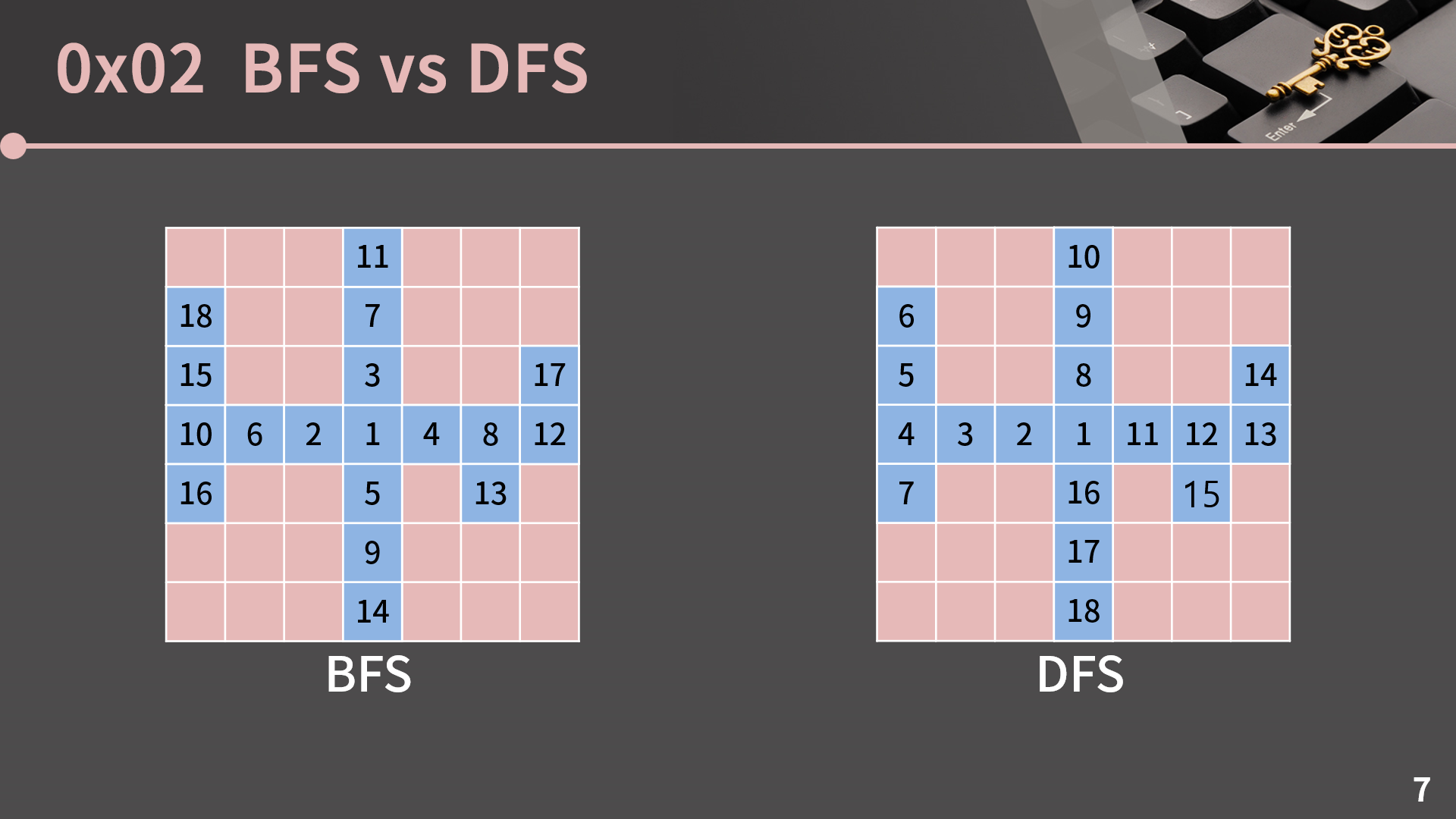
이렇게 BFS와 DFS를 살펴보면 BFS는 큐를 쓰고 DFS는 스택을 쓴다는 차이가 있지만 원소 하나를 빼내고 주변을 살펴본다는 알고리즘의 흐름은 똑같습니다. 하지만 둘의 방문 순서는 큰 차이가 있는데 우선 BFS에서의 방문 순서를 확인해보겠습니다. 시작점을 중앙으로 잡았는데 보면 마치 냇가에 던진 돌로 인해 동심원이 생기는 것 처럼 상하좌우로 퍼져나가는 것을 볼 수 있습니다. 그리고 이전 단원에서 다룬 BFS의 성질인 거리 순으로 방문한다는 것 또한 잘 성립함을 알 수 있습니다. 이번에는 DFS에서의 방문 순서를 확인해보겠습니다. 이건 어떻게 비유를 해야할지 모르겠긴 한데 아무튼 뭔가 차이가 있다는건 알 수 있을 것입니다. 뭔가 한 방향으로 막힐 때 까지 쭉 직진을 한다는걸 알 수 있습니다. 지금 보신 것과 같이 BFS와 DFS는 방문 순서에 큰 차이가 있습니다.

그리고 BFS에서 유용하게 썼던 "현재 보는 칸으로부터 추가되는 인접한 칸은 거리가 현재 보는 칸보다 1만큼 더 떨어져있다"는 성질이 DFS에서는 성립하지 않습니다. 이 그림은 (0, 0)에서 DFS를 시작할 때 나오는 상황인데, 빨간색 칸은 거리가 4인 반면 검정색 칸은 거리가 3입니다. 그래서 거리를 계산할 때에는 DFS를 사용할 수 없습니다. 그러면 결국 우리는 다차원 배열에서 굳이 BFS 대신 DFS를 써야하는 일이 없습니다. Flood Fill은 BFS와 DFS 중에서 어느 것을 써도 상관없는데 거리 측정은 BFS만 할 수 있으니 BFS 대신 DFS를 쓸 일이 없습니다. 그래서 앞으로 다차원 배열에서 순회하는 문제를 풀 때 계속 BFS만 짜게 됩니다. 하지만 그렇다고 해서 DFS가 아예 무쓸모한건 아니고 나중에 그래프와 트리라는 자료구조를 배울 때 DFS가 필요하게 됩니다. 그러니 아예 잊어버리지는 마시고 DFS는 스택을 써서 다차원 배열의 순회를 처리하는 알고리즘이다, 깊이를 우선해서 탐색한다는데 깊이가 무슨 의미인지는 아직 잘 와닿지 않는다 정도로만 기억하고 넘어가면 이번 단원에서 해야할 내용은 다 했습니다.

이로써 다차원 배열에서의 BFS와 DFS를 해결했습니다. 앞 슬라이드에서 열심히 설명했지만 굳이 BFS말고 DFS로 풀어야 하는 문제가 있지 않아서 따로 이번 단원과 연계되는 문제를 두지는 않았습니다. BFS 파트의 문제를 마저 푸시면 됩니다. 다음 단원은 재귀인데 재귀에서 어려움을 겪는걸 많이 봤어서 조금 걱정이 됩니다. 재귀를 한 번쯤은 들어보셨을테지만 막상 그걸 가지고 문제를 풀려고 하면 정말 까다로울 수 있습니다. 그러니까 다음 강의를 듣기 전에 재귀의 기본적인 개념이라도 한 번 보고 오시면 좋겠습니다. 예를 들어 재귀로 N부터 1까지 출력하기 내지는 1부터 N까지의 합 구하기 이런 문제를 풀어보면서요. 그럼 다음 시간에 만납시다.
'강좌 > 실전 알고리즘' 카테고리의 다른 글
| [실전 알고리즘] 0x0D강 - 시뮬레이션 (165) | 2020.07.17 |
|---|---|
| [실전 알고리즘] 0x0C강 - 백트래킹 (114) | 2020.07.06 |
| [실전 알고리즘] 0x0B강 - 재귀 (84) | 2020.06.14 |
| [실전 알고리즘] 0x09강 - BFS (322) | 2020.05.09 |
| [실전 알고리즘] 0x08강 - 스택의 활용(수식의 괄호 쌍) (37) | 2020.03.20 |
| [실전 알고리즘] 0x07강 - 덱 (39) | 2020.03.14 |